Раскрытие неопределённостей

Более сложные случаи при решении задач на пределы - если подстановка предельного значения аргумента в функцию приводит к неопределённым выражениям, символически обозначаемым как 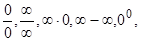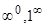. Нахождение предела в этом случае называется раскрытием неопределённости. Рассмотрим элементарные приёмы раскрытия неопределённостей.

4.5.3.1. Неопределённость . а). Дробно-рациональные функции. В этом случае в числителе и знаменателе выделяется множитель (х - а) и и рассматривается выражение, получаемое после сокращения на этот множитель. Пример: .

б). Дробно-иррациональные функции (. f (х) зависит от выражений вида 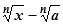). Множитель (х - а) в этом случае выделяется применением формул сокращённого умножения: и т.д.

в). Пределы от функций, в которых участвуют тригонометрические выражения, обычно сводятся к первому замечательному пределу: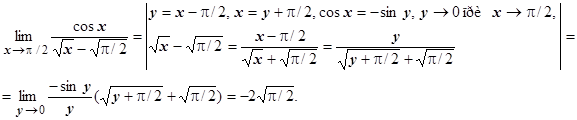

4.5.3.2. Неопределённость 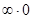формально легко сводится к неопределённости : пусть f (x)®¥, g (x)®0 при х ® а. Тогда 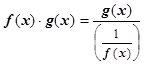и получена неопределённость (представление даст неопределённость 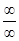, см. ниже). Однако часто можно обойтись более простыми преобразованиями: 4.5.3.3. Неопределённость 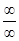также легко сводится к неопределённости : пусть f (x)®¥, g (x)®¥ при х ® а. Тогда 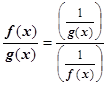и получена неопределённость . И здесь обычно обходятся более простыми преобразованиями, например, делением числителя и знаменателя на максимальную степень х (приём, применённый также в примере 7 раздела 4.5.2. Выделение главной части функции): , так как 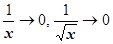при х ®+¥, при х ®¥ (теор.4.4.7 о произведении БМ на ограниченную функцию).

4.5.3.4. Неопределённость ¥-¥ также можно свести к предыдущим случаям: если f (x)®¥, g (x)®¥ при х ® а, то 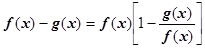. Дробь даёт неопределённость 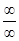. Если , получаем неопределённость 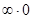, в других случаях неопределённость отсутствует. И здесь часто поступают по другому. Пример: 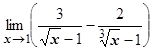. Чтобы избавиться от иррациональностей, перейдём к переменной у, связанной с х соотношением 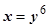. При х ®1 и у ®1, поэтому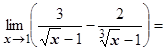

4.5.3.5. Показательно-степенные неопределённости 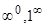сводятся к неопределённости 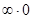следующим образом: (убедитесь, что во всех трёх случаях в показателе экспоненты получится неопределённость 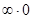). Однако неопределённости ("типа е ") часто сводят непосредственно ко второму замечательному пределу: пример 1.

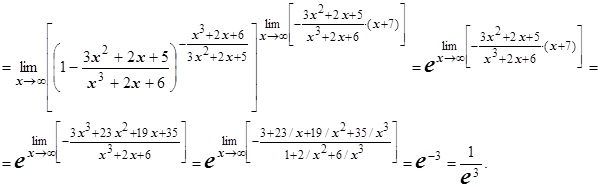
Пример 2.

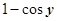Здесь мы заменили БМ на эквивалентную у ²/2 (ф.2 табл.4.4.10 и теор.4.4.9.2 о замене БМ на эквивалентные).

Несколько примеров на представление функции в виде :

3. : 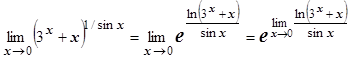(пользуемся непрерывностью функции ). Рассмотрим предел, находящийся в показателе степени: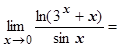

Возвращаемся к исходному пределу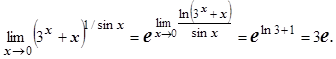

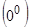
4. 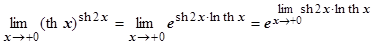. Предел, находящийся в показателе степени:

(пример 4 раздела 4.5.1). Окончательно: .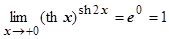

5.

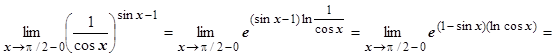
. Предел в показателе степени:

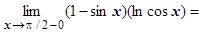
. Рассмотрим эти пределы по отдельности. Второй 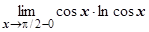после замены , у ®+0 при х ®p/2-0, опять сводится к примеру 4 раздела 4.5.1 и равен нулю. Первый представляет собой неопределённость , раскроем её:

Ответ:

4.5.3.6. Как уже говорилось, выделение главной части функции в совокупности с теор.4.4.9.2 о замене БМ и ББ на эквивалентные - наиболее мощный приём при решении задач на вычисление пределов. Пример: выделив главные части числителя и знаменателя, найти

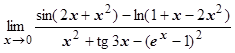. Решение: ~= x, ~~ ~~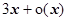3 x, поэтому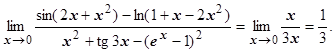

Примеры с использованием полученных в разделе 4.5.2 главных частей:

(примеры 1 и 3);

(примеры 2 и 4) и т.д.

Дата добавления: 2014-01-11