
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема непрерывности композиции непрерывных функций
 |
 Если функция
Если функция 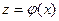 непрерывна в т.
непрерывна в т.  , а функция
, а функция 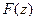 непрерывна в т.
непрерывна в т. 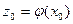 то сложная функция
то сложная функция  непрерывна в т.
непрерывна в т.  .
.
 К условиям теоремы 2 здесь добавляется непрерывность функции
К условиям теоремы 2 здесь добавляется непрерывность функции  в т.
в т.  . Учитывая это и применяя теорему 2 имеем
. Учитывая это и применяя теорему 2 имеем 
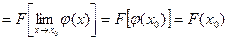
Доказанная теорема, наряду с теоремами 1 и 2 (см. пред. лекцию) систематически используются при вычислении предела непрерывных ункций.
Приращение аргумента и функции в точке, равносильное определение непрерывности.
 | |||
 | |||
М












 - приращение аргумента в т.
- приращение аргумента в т. 
 - приращение функции в т.
- приращение функции в т. 
 - приращение значения функции.
- приращение значения функции.

Пусть функция  непрерывна в т.
непрерывна в т.  , тогда
, тогда
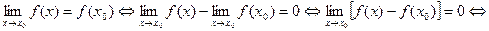
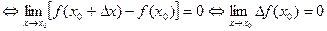
Таким образом можно дать определение непрерывности функции  в т.
в т.  в следующей равносильной форме:
в следующей равносильной форме:
Определение
Функция  называется непрерывной в т.
называется непрерывной в т.  если бесконечно малое приращение аргумента в т.
если бесконечно малое приращение аргумента в т.  вызывает бесконечно малое приращение функции в этой точке.
вызывает бесконечно малое приращение функции в этой точке.
Непрерывность элементарных функций.
Можно доказать, что все основные элементарные функции непрерывны в области их определения.
Сделаем на примере  .
.
Пусть х – произвольная фиксированная точка числовой оси. Рассмотрим приращение функции в т. х, т.е. 
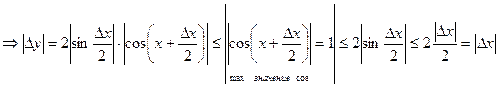
При этом использовано неравенство 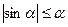 , для
, для 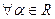
Ниже будет показано, что 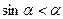 при
при 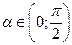 , что можно записать также в виде
, что можно записать также в виде 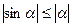
Это последнее неравенство не изменится при замене 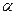 на
на  . Следовательно при
. Следовательно при  будет
будет  . Это последнее неравенство очевидно верно и при
. Это последнее неравенство очевидно верно и при 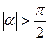 , т.к.
, т.к.  , а
, а  .
.
Итак получено:
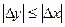 , что можно записать также в виде
, что можно записать также в виде  . Тогда
. Тогда 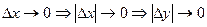 (использована теорема о двух легавых)
(использована теорема о двух легавых) 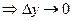 , т.е.
, т.е. 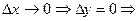 функция
функция  непрерывна в т. х.
непрерывна в т. х.
А т.к. точка  выбрана произвольно, то заключаем, что функция
выбрана произвольно, то заключаем, что функция  непрерывна на всей числовой оси.
непрерывна на всей числовой оси.
Элементарной функцией называется всякая функция составленная из основных элементарных функция при помощи конечного числа арифметических действий и композиций.
|
|
|
Так как основные элементарные функции непрерывны в области их определений, а сложение, вычитание, умножение, и деление и композиция непрерывных функций приводят к непрерывным функциям, то заключаем, что всякая элементарная функция непрерывна в области определения.
Два замечательных предела.
Покажем, что  (1)
(1)
Где х – измеряется в радианах.

 Рассмотрим окружность радиуса R=1 и центральный угол
Рассмотрим окружность радиуса R=1 и центральный угол 
A
Х 0 С В D
| 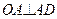 т.к. хорда окружности меньше стягиваемой ею дуги, т.е. т.к. хорда окружности меньше стягиваемой ею дуги, т.е.  , откуда , откуда  , т.е. , т.е. 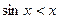 , для , для 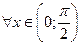
|
С другой стороны площадь кругового сектора ОАВ меньше площади
меньше площади 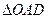 .
. 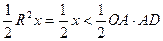 или
или  . Поэтому
. Поэтому  для
для  т.к.
т.к. 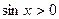 для
для 
 или
или  (2)
(2)
Эти последние неравенства не изменятся при замене х на –х, т.е. они будут справедливы в проколотой  - окрестности т. х=0.
- окрестности т. х=0.
 Так как функция
Так как функция  непрерывна в т. х=0, т.е.
непрерывна в т. х=0, т.е. 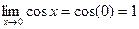 , то из неравенств (2) с учетом теоремы о lim двух легавых вытекает формула (1).
, то из неравенств (2) с учетом теоремы о lim двух легавых вытекает формула (1).
Примеры:
1) 
2) 
ЛЕКЦИЯ № |
 Т.е. формула (2) полностью доказана.
Т.е. формула (2) полностью доказана.
Полагая в формуле 2 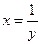 (если
(если 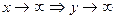 ) и применяя теорему о замене переменной в пределе получим другое представление 2 замечательного предела:
) и применяя теорему о замене переменной в пределе получим другое представление 2 замечательного предела:
 (2’)
(2’)
Следствия:
1) 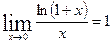 (3) - третий замечательный предел.
(3) - третий замечательный предел.
Запишем второй замечательный предел по формуле (2’) в виде.
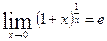
 и прологарифмируем его по основанию e:
и прологарифмируем его по основанию e: 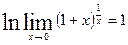 здесь
здесь  так как функция ln(u) непрерывна в точке u=e, то переставляя местами знак предела и знак непрерывной функции получим:
так как функция ln(u) непрерывна в точке u=e, то переставляя местами знак предела и знак непрерывной функции получим:  или
или 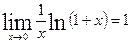
2) 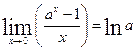 (4)
(4)
здесь  в частности при
в частности при 
 (4’)
(4’)
 Положим
Положим 
Откуда 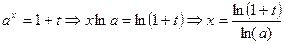 ; при
; при  т.к. показательная функция
т.к. показательная функция  непрерывна в точке x= 0. Пользуясь теоремой о замене переменной в пределе и формулой (3) имеем
непрерывна в точке x= 0. Пользуясь теоремой о замене переменной в пределе и формулой (3) имеем
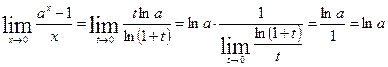
 Полагая в формуле (4) a = e приходим к формуле (4’)
Полагая в формуле (4) a = e приходим к формуле (4’)
3)  где
где 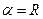

Положим 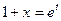 (при
(при  в силу непрерывности экспоненциальной функции)
в силу непрерывности экспоненциальной функции)  ;
; 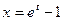 Имеем:
Имеем:
Применяя теорему о замене переменной в пределе и формулу (4’).
|
|
|

 Показательно-степенная функция.
Показательно-степенная функция.
Для вычисления пределов функций вида 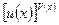 следует пользоваться формулой:
следует пользоваться формулой:
 (6)
(6)
 При этом считаем, что
При этом считаем, что 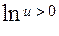 и
и 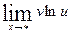 существует.
существует.
 Достаточно применить основное логарифмическое тождество и непрерывность экспоненциальной функции.
Достаточно применить основное логарифмическое тождество и непрерывность экспоненциальной функции.
 Часто встречается случай когда
Часто встречается случай когда 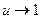 при
при 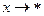 Покажем, что формула (6) принимает вид:
Покажем, что формула (6) принимает вид: 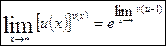 (7)
(7)
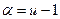 (
(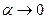 при
при 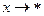 )
)
Имеем:  применяя формулу (3) и
применяя формулу (3) и 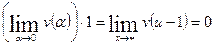 . Особенно часто формула (7) применяется когда
. Особенно часто формула (7) применяется когда  , т.е. для раскрытия неопределенности
, т.е. для раскрытия неопределенности 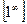 .
.
Примеры применения формул.
1) 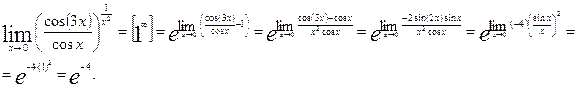
2)

Сравнение Б.М.Ф.
Пусть 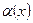 ,
, 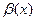 - б.м. при
- б.м. при 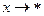
Рассмотрим: Если
Если 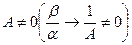 , то говорят что б.м.
, то говорят что б.м. 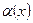 и
и 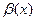 - одинакового порядка малости, в частности, если
- одинакового порядка малости, в частности, если 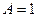 , то
, то 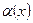 и
и 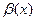 называются эквивалентными бесконечно малыми, что записывается в виде
называются эквивалентными бесконечно малыми, что записывается в виде 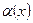
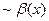 (в окрестности
(в окрестности 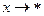 ).
).
Например при 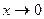 :
:
1) 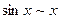
2) 
3) 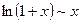 в силу формулы (3)
в силу формулы (3)
4)  (в частности
(в частности 
5)  (в частности
(в частности 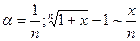
Если  , то говорят что
, то говорят что 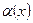 является б.м. высшего порядка малости, чем
является б.м. высшего порядка малости, чем 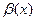 или, что
или, что 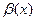 является б.м. низшего порядка малости, чем
является б.м. низшего порядка малости, чем 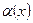 . Это обстоятельство записывается в виде:
. Это обстоятельство записывается в виде: 
 есть “о малое” от
есть “о малое” от  .
.
Например: 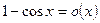 при
при 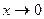 .
.
Теоремы об эквивалентных б.м.
Теорема 1
Пусть 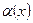 ,
, 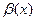 ,
,  - б.м. при
- б.м. при 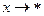 причем
причем 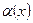 ,
, 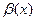 - одного порядка; а
- одного порядка; а  тогда
тогда 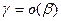 .
.


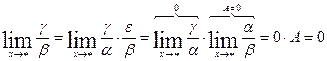 т.е.
т.е. 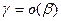 .
.
Теорема 2
Для того, чтобы две б.м. при одном и том же стремлении x были эквивалентны необходимо и достаточно, чтобы их разность была б.м. более высокого порядка, чем каждая из них.


Обратно  , т.е.
, т.е. 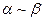
 Применяя теорему 1 видим, что соотношение
Применяя теорему 1 видим, что соотношение 
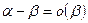 так же имеет место.
так же имеет место.
Теорема 3
Предел отношения двух б.м. не изменится, если одну из них или обе заменить на эквивалентную ей б.м.
 Пусть
Пусть 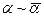 , а
, а  при
при 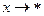 имеем
имеем


 Теорема 4 (принцип отбрасывания б.м. высшего порядка)
Теорема 4 (принцип отбрасывания б.м. высшего порядка)
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 1642; Нарушение авторских прав?; Мы поможем в написании вашей работы!

