Если , то

Это есть следствие теоремы 2.

ЛЕКЦИЯ №

Примеры применения теорем:

1)

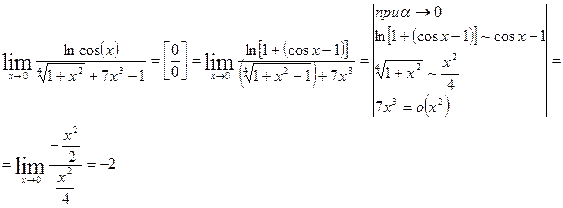
Определение.

Если 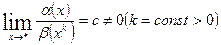то говорят, что б.м. α имеет порядок k относительно б.м.. Из этого определения следует, что б.м.имеет 1-й порядок малости относительно себя.

Обычно в качестве «масштабной б.м. b» выбирают простейшую б.м. равную х-а при 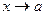, или равную при .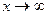

Имеем:

Б.м. называется главной частью б.м. .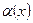

Примеры:

Пусть “масштабной” б.м. является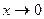

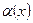1) главная часть б.м. и 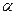имеет 6-й порядок малости относительно x.

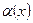2) главная часть б.м. и 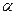2-го порядка малости относительно x.

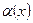3) главная часть б.м. и 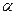имеет относительно x порядок .

Аналогично сравнению б.м. проводится и сравнение б.б. при .

Только здесь говорят о более высоком или более низком порядке роста одной б.б. относительно другой или же об одинаковом порядке роста двух б.б. В частности: две б.б. функции называют эквивалентными при , если их предел их частного равен 1 при .

Пример:

Пусть масштабная б.б., а 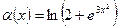при 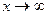нужно найти: главную часть .

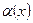- главная б.б. 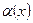и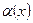

имеет 2-й порядок роста относительно .

Не следует думать, что любые две б.м. (любые две б.б.) можно сравнить между собой.

Пример: б.м. 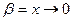и несравнимы между собой при 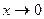, т.к. не существует.

Свойства функций непрерывных на отрезке. Непрерывность обратной функции.

Функции, непрерывные на отрезке обладают рядом свойств, которые, вообще говоря не присущи функциям непрерывных на других промежутках.

Теорема1.

Если функция f(x) непрерывна на отрезке [a,b], то она ограничена на этом отрезке.

Теорема 2. (Вейерштрасса)

Среди значений непрерывной на отрезке [a,b] функции f(x) существует наименьшее (m) и наибольшее (М)

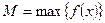
Теорема 3.

Пусть 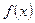непрерывна на отрезке [a,b] и , тогда найдется хотя бы хотя бы одна точка для любого значения С между A и B , для которой . Иными словами функция f(x) принимает любое промежуточное значение между двумя данными. В частности если А и В – числа противоположных знаков, то полагая С=0, получим f(с)=0 (теорема об обращении в 0 непрерывной на отрезке функции, принимающей на концах отрезка значения разных знаков).

Другое следствие теоремы 3.

Непрерывная на отрезке [a,b] функция принимает по крайней мере один раз любое промежуточное значение между m и М

Теорема 4.

Если ф-ия y=f(x) непрерывна и строго возрастает(строго убывает) на отрезке [a,b] то обратная ей функция x=g(x), существует, непрерывна и строго возрастает (убывает) на отрезке [m,M]

Точки разрыва функции. Их классификации.

Определение 1.

x=a называется точкой разрыва функции y=f(x) если не имеет место равенство

f(a-0)=f(a+0) = f(a)

Пусть точка а – точка разрыва функции f(x).

Если существуют односторонние пределы f(a-0), f(a+0) и они конечны, то точка а называется Точкой разрыва первого рода.

Если при этом f(a-0)=f(a+0), т.е. в т. а функция имеет предел, то точка а называется точкой устранимого разрыва. В этом случае разрыв в точке а может быть устранен, если положить 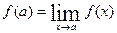, такая процедура продолжением функции по непрерывности, преобразованная таким образом функция является непрерывной в точке а.

Определение 3.

x=a называется точкой разрыва 2-го рода функции f(x), если точка не является точкой разрыва 1-го рода, другими словами в точке разрыва 2-го рода хотя бы один из односторонних пределов функции f(a+0) или f(a-0) не существует или бесконечен.

Пример 1.

Дата добавления: 2014-01-11