
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема. Пусть функции y=f(x) удовлетворяет всем условиям теоремы о обратной функции и имеет в точке производную
|
|
|
|
Пусть функции y=f(x) удовлетворяет всем условиям теоремы о 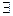 обратной функции
обратной функции  и имеет в точке
и имеет в точке 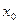 производную
производную 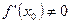 , тогда обратная функция
, тогда обратная функция  так же имеет производную в соответствующей точке
так же имеет производную в соответствующей точке 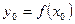 и справедлива формула
и справедлива формула 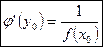 (6).
(6).

Дадим аргументу y обр. ф-ции в точке 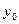 приращение
приращение 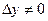 тогда в силу строгой монотонности обр. ф-ции ее приращение
тогда в силу строгой монотонности обр. ф-ции ее приращение  в точке
в точке 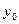 будет отлично от 0 и поэтому можно записать
будет отлично от 0 и поэтому можно записать 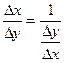 . Перейдем в этом равенстве к пределу при
. Перейдем в этом равенстве к пределу при 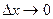 (при этом
(при этом 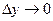 в силу непрерывности функции y=f(x) в т.
в силу непрерывности функции y=f(x) в т. 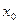 ).
).
 Следовательно предел слева также
Следовательно предел слева также 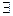 и по определению производной есть производная
и по определению производной есть производная  .
.
 Окончательно:
Окончательно:  .
.
Геометрическая иллюстрация.

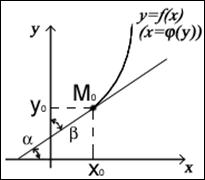 имеем:
имеем:
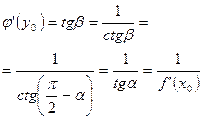
Производные основных элементарных функций.
1. 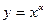 , где
, где 
 (7) эта формула будет доказана позже.
(7) эта формула будет доказана позже.
2.
 ; (8) ; (8)

| 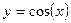 (9) (9)
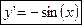
|
формулы (8) и (9) доказываются с помощью определения производной, 1 замечательного предела и непрерывности функции cos(x) и sin(x) соответственно.
3.
y=tg(x);
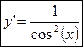 где
где 
| y=ctg(x)

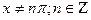
|
Формулами (10) и (11) доказываются с использованием правила дифференцирования частного и формул (8) и (9).
 4.
4. 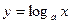 где
где 
 (12)
(12)
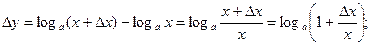
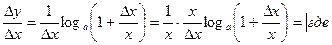
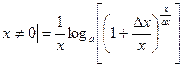 ; перейдем к lim при
; перейдем к lim при 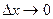 пусть
пусть  при
при 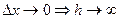
 (2-ой замечательный предел). Поэтому с учетом непрерывности логарифмической функции
(2-ой замечательный предел). Поэтому с учетом непрерывности логарифмической функции 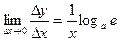 или
или 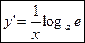 , если a=e
, если a=e 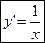 .
.

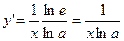 .
.
5.
 y=arcsin(x) y=arcsin(x)
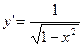 (13) (13)
| y=arccos(x)
 (14) (14)
|
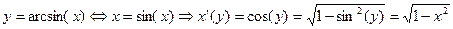 т.к. на
т.к. на 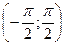
 то корень арифметический по теореме о производной обратной функции
то корень арифметический по теореме о производной обратной функции 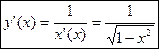 (13). Формула (14) доказывается аналогично или с помощью
(13). Формула (14) доказывается аналогично или с помощью

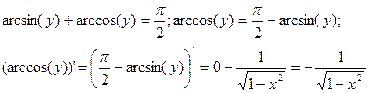
6.
 y=arctg(x) y=arctg(x)
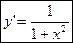 (15) (15)
| y=arcctg(x)
 (16) (16)
|

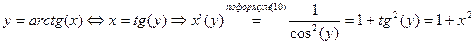 по теореме о производной обратной функции
по теореме о производной обратной функции  .
.
Формула (16) доказывается аналогично.
7.  где
где 
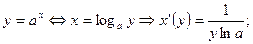 по теореме о производной обратной функции имеем
по теореме о производной обратной функции имеем  таким образом
таким образом  ;
; 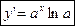 (17).
(17).
В частности, если a=e,  (18).
(18).
8.
y=sh(x)
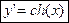 (19) (19)
| y=ch(x)
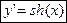 (20) (20)
|

Доказательство формулы (20).
Имеем  .
.
 Формула (19) доказывается аналогично.
Формула (19) доказывается аналогично.
9.

 (21) (21)
| 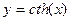
 (22) (22)
|
При доказательстве используется производная частного, а потом формулы (19) и (20).
|
|
|
Логарифмическое дифференцирование.
Определение.
Логарифмической производной функции y=f(x) называется производная ее логарифма.
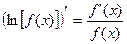
тогда производная функции y=f(x) может быть найдена так: 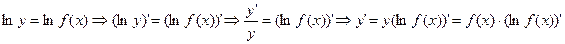 .
.
Рассмотрим степенную функцию
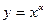
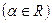
Имеем 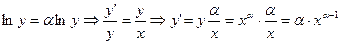 тем самым формула (7) доказана.
тем самым формула (7) доказана.
Применив прием логарифмического дифференцирования, мы можем вычислить производную показательно-степенной функции 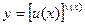 .
.
Имеем, функции u(x) v(x) дифференцируемыми в т. x, а функцию u(x)>0 в некоторой окрестности т. x: 
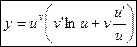 (23).
(23).
Правило логарифмического дифференцирования рекомендуется применять на практике при дифференцировании произведения многих сомножителей.
Дифференцирование неявной функции.
Рассмотрим уравнение F(x,y)=0 относительно y.
При некоторых условиях это уравнение определяет единственную функцию  называемая неявной функцией, задаваемая исходной функцией. Тогда
называемая неявной функцией, задаваемая исходной функцией. Тогда 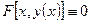 .
.
 при дифференцировании применим теорему о производной сложной функции. В результате получиться линейное уравнение относительно y’ уравнение, решая которое находим y’.
при дифференцировании применим теорему о производной сложной функции. В результате получиться линейное уравнение относительно y’ уравнение, решая которое находим y’.
………………………………………………………………………………………………..
Примечания.
1) Если производные 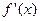 и
и  удовлетворяют всем условиям доказанной теоремы, то правило Лопиталя-Бернули может быть повторено.
удовлетворяют всем условиям доказанной теоремы, то правило Лопиталя-Бернули может быть повторено.
2) Правило Лопиталя остается оправданным если 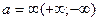 .
.
| ЛЕКЦИЯ № |
3) Предел отношения функции  может $ и без того, чтобы $ предел относительно их производных.
может $ и без того, чтобы $ предел относительно их производных.
4) Правило Лопиталя-Бернули остается в силе, когда 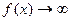 и
и  при
при 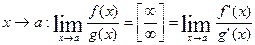 . Итак, правило Лопиталя-Бернули, когда оно применимо позволяет раскрыть неопределенности типов:
. Итак, правило Лопиталя-Бернули, когда оно применимо позволяет раскрыть неопределенности типов: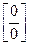 и
и 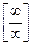 .
.
5) Сравнение при помощи правила Лопиталя-Бернули поведения при 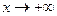 функции: показательно
функции: показательно  , степенной
, степенной 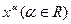 и логарифмической
и логарифмической  показывают, что показательная функция имеет более высокий порядок роста, чем степенная – более высокий порядок роста чем логарифмическая.
показывают, что показательная функция имеет более высокий порядок роста, чем степенная – более высокий порядок роста чем логарифмическая.  .
.
|
|
|
Другие типы неопределенностей.
1)  или же
или же 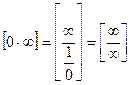 и применяется правило Лопеталя-Бернули.
и применяется правило Лопеталя-Бернули.
2) 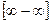
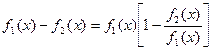 , если
, если 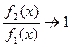 при
при 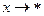 ,
,  - ББ при
- ББ при 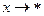 , если же
, если же  при
при 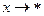 , то имеем неопределенность типа
, то имеем неопределенность типа 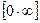 .
.
Неопределенности типов 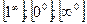 раскрываются с помощью предварительного логарифмирования и вычисления предела логарифма функции
раскрываются с помощью предварительного логарифмирования и вычисления предела логарифма функции 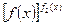 что приводит к неопределенности типа
что приводит к неопределенности типа 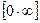 .
.
Примеры.
1) 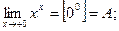

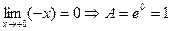
2)  .
.
Рассмотрим:  |это отношение не имеет предела при
|это отношение не имеет предела при 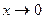 |
|  Þ правило Лопиталя-Бернули не применимо. Найдем предел А непосредственно.
Þ правило Лопиталя-Бернули не применимо. Найдем предел А непосредственно. 
 0
0
Теорема Тейлора.

 Пусть функция
Пусть функция 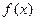 имеет в некоторой окрестности конечной точки a производные до порядка
имеет в некоторой окрестности конечной точки a производные до порядка  включительно, x – любое значение аргумента из указанной окрестности
включительно, x – любое значение аргумента из указанной окрестности 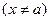 тогда между точками a и x найдется точка x такая, что
тогда между точками a и x найдется точка x такая, что 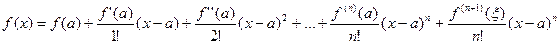
(5)
 многочлен Тейлора функции
многочлен Тейлора функции 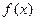
Формула (5) называется формулой Тейлора с остаточным членом в форме Лагранжа: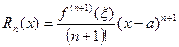 ;
; 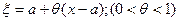 , формула Тейлора с центром в точке a. Формулу Тейлора часто записывают в другом виде.
, формула Тейлора с центром в точке a. Формулу Тейлора часто записывают в другом виде.
Положим 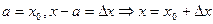 .
.
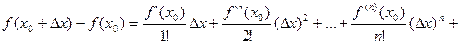
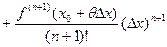 , отсюда при n=0 получается формула Лагранжа
, отсюда при n=0 получается формула Лагранжа  .
.
Таким образом формула Тейлора обобщает формулу Лагранжа. Покажем, что если функция  ограничена в окрестности точки a, то остаточный член формулы Тейлора есть БМ более высокого малости, чем
ограничена в окрестности точки a, то остаточный член формулы Тейлора есть БМ более высокого малости, чем 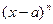 при
при 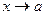


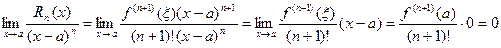
т.о. 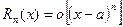 ; (при
; (при 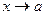 ) (6).
) (6).
Остаточный член (6) называется остаточным членом в форме Пеано, а формула Тейлора с остаточным членом в форме Пеано называется локальной формулы Тейлора. Формула Тейлора при a=0 (с центром в 0) называется формулой Маклорена.
 . (7)
. (7)
Где остаточный член имеет: в форме Лагранжа 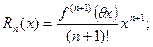
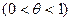
в форме Пеано 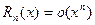 .
.
Разложение по формуле Маклорена некоторых элементарных функций.
I. 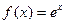
т.к. 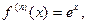
 , для
, для 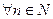 , то формула Маклорена имеет вид
, то формула Маклорена имеет вид 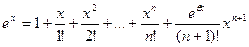 . (8)
. (8)
На любом отрезке 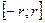 , где
, где 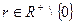 в силу того, что:
в силу того, что: 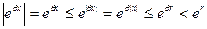 , т.е.
, т.е. 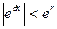 , получаем следующую оценку следующего члена
, получаем следующую оценку следующего члена 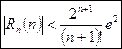 (9)
(9)
Полагая здесь x=r=1 имеем оценку погрешности приближенного вычисления числа e 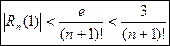 (9’)
(9’)
II. 
т.к. 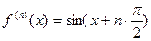 ,
,

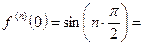
 то формула Маклорена имеет вид
то формула Маклорена имеет вид 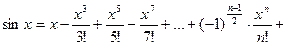
 ; (10).
; (10).
Здесь n – нечетное число x – в радианах. Очевидно, что на любом отрезке  справедлива следующая оценка остаточного члена:
справедлива следующая оценка остаточного члена: 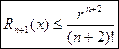
(11)
III. 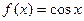
Т.к. 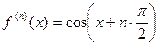 ;
;  , то формула Макло-рена имеет вид:
, то формула Макло-рена имеет вид: 
 ;
;
(12).
Здесь n – четное число на любом отрезке  имеет очевидно для остаточного члена оценку (11).
имеет очевидно для остаточного члена оценку (11).
IV. 
Т.к. 
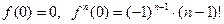 , то формула Маклорена имеет вид:
, то формула Маклорена имеет вид:
|
|
|
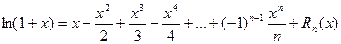 (13)
(13)
где остаточный член имеет вид:
 в форме Лагранжа. (14)
в форме Лагранжа. (14)
для значений 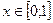 имеем оценку, переходя в (14) к модулям:
имеем оценку, переходя в (14) к модулям:
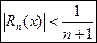 ; (15)
; (15)
Для значений 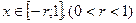 можно доказать, что имеет место оценка:
можно доказать, что имеет место оценка:
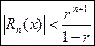 (16).
(16).
| ЛЕКЦИЯ № |
V.  , где
, где 
Т.к 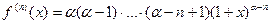
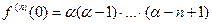 , то формула Маклорена имеет вид:
, то формула Маклорена имеет вид:

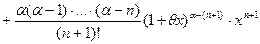 ; (17)
; (17)
В частности когда  (натуральное число), то получаем формулу бинома Ньютона:
(натуральное число), то получаем формулу бинома Ньютона: 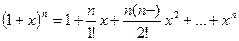 .
.
Примеры:
1) Вычислить приближенно  с помощью дифференциала и оценить погрешность этого приближения.
с помощью дифференциала и оценить погрешность этого приближения.
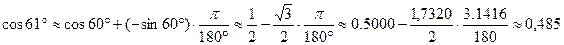
Запишем теперь формулу Тейлора с n=1
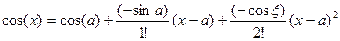 (положим здесь a=60°, x=61°, тогда
(положим здесь a=60°, x=61°, тогда  ) имеем:
) имеем:
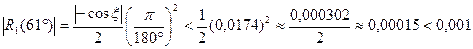
предыдущее вычисление проведено с точностью до одной тысячной, таким образом 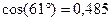 с точностью 0,001.
с точностью 0,001.
2) при каких x справедливо с точностью до 0б0001 приближенная формула  .
.
Погрешность этой приближенной формулы согласно (12)  , откуда:
, откуда:  таким образом приближенная формула при заданной точности вычислений, справедлива для таких x, что
таким образом приближенная формула при заданной точности вычислений, справедлива для таких x, что 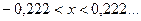
3) Вычислить 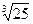 с точностью 0,001
с точностью 0,001
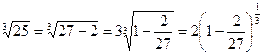 здесь
здесь 
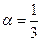
Оценивая остаточный член в формуле (17) 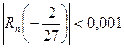 , находим, что достаточно взять n=2; тогда:
, находим, что достаточно взять n=2; тогда:  и
и 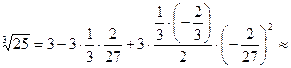 |проделывая это и округляя до 3-го знака|» 2,926 (с точностью до 0,001).
|проделывая это и округляя до 3-го знака|» 2,926 (с точностью до 0,001).
Локальные формулы Тейлора.
Локальная формула Тейлора-Маклорена позволяет эффективно исследовать поведение функции в окрестности данной точки, в частности вычисляя
запишем ее для элементарной функций + (асимптотическое разложение).
I. 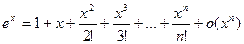
II. 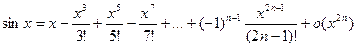
III. 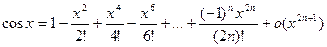
IV. 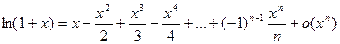
V. 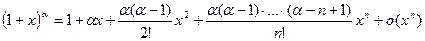
Вычислить:

Имеем:


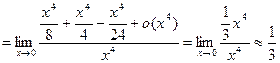
Теоремы об возрастании и убывании дифференцируемых функций. Экстремумы.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 576; Нарушение авторских прав?; Мы поможем в написании вашей работы!