Полиномиальная сводимость. NP-полные задачи

Одна и та же математическая задача распознавания может быть фор­мализована с использованием разных алфавитов и разных способов кодирования. Тем не менее, если речь, например, идет о некото­рой арифметической задаче, то можно ожидать, что основание q е N, q ^ 2, выбранной позиционной системы счисления не будет влиять на принадлежность соответствующего предиката классу Р, так как размеры [log„ (n + l)l, [log„ (п + 1)1 записей числа п в двух разных системах счисления являются величинами одного порядка, и сам пе­реход от одной записи к другой может быть выполнен за время, огра­ниченное полиномом от размера входа.

Такого рода связь может существовать и между совершенно раз­ными задачами распознавания, формализованными с помощью пре­дикатов на словах.

Определение 32.1. Пусть v и v —предикаты на словах в алфавитах Л, Л. Говорят, что v полиномиально сводится к v, и пишут v ^_р v, если существует такая функция /еР, /: Л*—>Л*, что v (x) = v (/(x)).

Из того, что для / е Р длина слова /(х) как функция от дли­ны слова х полиномиально ограничена, а также из того, что ком­позиция двух полиномов р₃(£) = Pi(P2(0) вновь является полиномом (при этом если p i(t), p ₂(0 имеют неотрицательные коэффициенты, то и р₃(£) тоже), мы получаем, что отношение ^_р транзитивно и что

v eP => v eP

при v ^_р V.

В 70-х годах прошлого столетия С. Кук доказал замечательную тео­рему о существовании в NP таких предикатов на словах, к каждому из которых полиномиально сводится любой предикат из NP. Приня­тая терминология такова:

Определение 32.2. Предикат и е NP называется №-полным, если v ^_р и для каждого v е NP.

§ 32. Полиномиальная сводимость. NP-полные задачи

Перед формулировкой теоремы Кука напомним, что любую булеву формулу от x_ъx₂,...,x_n можно задать в конъюнктивной нормальной форме (КНФ):

D₁AD₂A...AD_m, Di = (l_{i 1}v li ₂V...v l _{g ki} )_J i = l,2,...,m, (32.1)

при этом l_ij является литералом, т. е. некоторой переменной x_s или переменной с отрицанием ­ x_s. Каждую формулу, заданную в КНФ, можно изобразить словом из Л*, как обсуждалось в примере 30.1. Предикат, принимающий значение 1 на тех и только тех словах из Л*, которые являются кодами КНФ выполнимых формул, назовем Sat (от английского слова satisfiability, одно из значений которого —вы­полнимость).

Теорему Кука мы приводим без доказательства¹:

Теорема Кука. Предикат Sat является NP-полным.

Если показано, что некоторый предикат u является NP-полным, и при этом для некоторого другого предиката v е NP установлено, что u ^_p v, то из этого, очевидно, следует, что v тоже NP-полный.

Пример 32.1. Прямым следствием теоремы Кука является то, что рассмотренный в примере 30.1 предикат выполнимости произволь­ной, не обязательно заданной в КНФ, формулы является NP-полным. Полиномиальная сводимость предиката Sat к этому предикату оче­видна: в качестве функции f, фигурирующей в определении 32.1, можно взять функцию, которая преобразует слово x из Л* в скобку «)» или еще в какой-нибудь символ, не являющийся кодом какой-ли­бо булевой формулы, всякий раз, когда слово x не является кодом какой-либо КНФ, и преобразует x в x в противном случае (можно описать принадлежащий Р алгоритм вычисления f (x)).

Когда говорят о принадлежащих классам Р и NP задачах распо­знавания и о NP-полных задачах, а не о предикатах и языках, то при этом предполагают, что способ кодирования входных данных ясен из

¹ Мы опускаем доказательство этой теоремы, называемой в некоторых источниках также теоремой Кука—Левина, из-за того, что оно требует привлечения специфиче­ской техники доказательств утверждений о машинах Тьюринга; такого рода доказа­тельства выглядят естественно в определенном контексте, который отличается от кон­текста этого курса. Отчасти это послужило и причиной того, что в § 31 мы оставили без доказательства теорему Фишера—Рабина. Доказательство теоремы Кука имеется, на­пример, в [13], [4], [23]. Прозрачное изложение идей доказательства принадлежности классу NP предиката, распознающего выполнимость произвольной булевой формулы, и полиномиальной сводимости такого предиката к Sat можно найти в [10].

Глава 7. Сводимость

контекста и определен, по крайней мере, с точностью до полино­миальной сводимости. Обсуждая в дальнейшем задачи из примеров предыдущего параграфа, мы будем иметь в виду рассмотренные там способы кодирования.

Пример 32.2. Покажем сводимость задачи выполнимости КНФ к задаче о клике с указанным числом вершин (пример 30.3). Пусть КНФ F имеет вид (32.1). Построим граф G_F с k_г + k₂ +... + k_m верши­нами, для которых используем обозначения

l_ij, i = l,2, ...,m, j = l,2,...,k_h

при этом вершины l_ij и l_vw соединяем ребром, если и только если выполнены два условия:

• i # v,

• конкретные литералы, скрывающиеся в (32.1) за обозначениями l_ij и l_vw, не являются отрицанием друг друга (скажем, если l_ij —это ­ x_ъ а l_vw— это x_ъ то эти две вершины ребром не соединяются).

Построение матрицы смежности графа G_F может быть выполнено за полиномиально ограниченное время.

Из определения клики и способа построения графа G_F следует, что клика из m вершин в этом графе существует, если и только если формула (32.1) выполнима. В самом деле, при наличии такой клики полагаем x_s = 0, когда литерал ­ x_s соответствует одной из вершин клики, а в остальных случаях x_s = l. В результате каждое D_i в (32.1) равно 1.

Наоборот, если заданная формула (32.1) выполнима, то при со­ответствующих значениях всех переменных x_ъx₂, ■■■,x_n для каждого i^m можно выбрать j такое, что l_ij —это литерал со значением 1. Сделав такой выбор, мы получаем набор вершин, образующий клику с m вершинами.

Если исходная КНФ имеет вид

(- x ₁v- x ₂)A(x ₂)A(x ₁V x ₂),

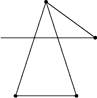
то мы получаем граф G_F с пятью вершинами (рис. 25), в котором обнаруживается клика C l n, l _2i, l ₃₂D с тремя вершинами. Это соответ­ствует тому, что исходная формула принимает значение 1 при x_г = 0, x ₂ = 1.

Задача распознавания существования в графе клики с заданным числом вершин является NP-полной.

г31

§ 32. Полиномиальная сводимость. NP-полные задачи
* 2 i г21

а)

б)

.hi

h2*

Дата добавления: 2014-01-11