Редукция

Определение.

Х сворачивается к YY -результат замены части Х вида (λх.M)N на [N/x]M:

X редуцируется к YY получается из Х с помощью конечной (возможно, пустой) последовательности сворачиваний и замен имен связанных переменных.

Выражение вида (λх.M)N называется редекс.

Подстановка N на место х в М [N/x]M называется сверткой.

λ выражение Р находится в нормальной форме, если не содержит ни одного редекса.

Пример. 1) λх.х - является нормальной формой

2)(λх.+х((λу.у)х)) → не является нормальной формой → (λх.+хх) - является нормальной формой.

Говорят, что терм Р редуцируется к терму Q, если существует доказательство такого выражения: Р → Q.

Теорема Черча-Россера:

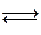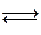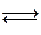Если х конвертируется к у, т.е. ху (х редуцируется к у: х→у) и х конвертируется (редуцируется) к z,то а: у→а и z→а (уа и zа)

Следствие:

У 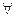λ - терма ! (единственная) нормальная форма.

Доказательство: (от противного)

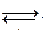Пусть у выражения x существует две нормальные формы a,b: х→a и х→b т.е. а,b (a ≠b): (ab)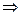

По Тh C: a→c, b→c 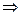т.к. а может редуцироваться, то а не является нормальной формой, то же самое можно сказать про b.

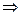Либо не редуцируются, либо совпадают.

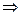Двух нормальных форм существовать не может. #

Если а редуцируется к b (а→b) и b редуцируется к а (b→a),то говорят что а и b

конвертируются одно в другое (а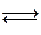b),т.е. а→b, b→a: а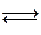b- взаимно конвертируются.

Теорема.

λ–теория не противоречива, т.е. в ней нельзя вывести любые утверждения.

Теорема: (О комбинаторной полноте).

Пусть λ- терм М содержит n свободных переменных х₁…х_n, тогда λ-терм F: х₁…x_n не являются свободными переменными F (X₁…X_n FV(F)) и при этом FX₁…X_n=M соответственно F=λx₁…x_n.M.

Погружение классических вычислений в λ-исчисление.

Определение:

Нумералы - объекты, обладающие свойствами натуральных чисел.

n = λxy.(xⁿ)y n =(SB)ⁿ(KI), здесь S,B,K,I - простейшие комбинаторы

Системы комбинаторов предназначены для выполнения тех же функций, что и системы

-l - конверсии

B: Bfgx = f(gx)- элементарный композитор

S: Sfgx = fx(gx) –элементарный коннектор

K: Kcx =c – элементарный канцелятор

I: Ix = x – комбинатор тождества

Пусть z₀= λyx.x (считаем это число нулем). Остальные целые числа введем по индукции: z_n+1=σz_n, где σ - функция добавления единицы: σ = λxyz.y(xyz)

Операция сложения PLUS:

PLUS = λxy.xσy

Утверждается, что PLUSz₀b=b и PLUS(σa)b=σ(PLUSab) (проверяется подстановкой).

Определение:

Усеченная разность: DIF=λxу.yπx, где π-функция предшествования

π=λx.хω(kz₀)z₁, где ω= λx.D(σ(xz₀))(xz₀) πz_i+1=z_i, i ≥ 0

k= λxy.x πz₀=z₀.

D - декартово замкнутое произведение.

D: PROD = λxy.x(yσ)z₀

TRUEλxy.x (так обозначим)

FALSEλxy.y

If X then Y else ZXYZ.

Дата добавления: 2014-01-11