
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Уравнение состояния вещества
|
|
|
|
В систему основных уравнений газовой динамики входит уравнение состояния среды. Конкретный вид уравнения состояния определяется либо из опыта, либо находится, в некоторых частных случаях, методами статистической физики. Для твердых и жидких тел разработаны полу эмпирические методы получения уравнений состояния. В основе определения такого уравнения лежат ударные ударные адиабаты твердых и жидких тел.
Уравнение состояния системы может быть задано, например, в форме:
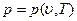 (1.5)
(1.5)
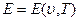 (1.6)
(1.6)
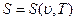 (1.7)
(1.7)
В этих уравнениях в качестве независимых переменных выбраны два параметра: удельный объем 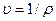 и температура Т. Уравнение (1.5) называется термическим уравнением состояния, поскольку с помощью этого уравнения определяется температура. Уравнение (1.6) называется калорическим уравнением состояния. Основное уравнение термодинамики
и температура Т. Уравнение (1.5) называется термическим уравнением состояния, поскольку с помощью этого уравнения определяется температура. Уравнение (1.6) называется калорическим уравнением состояния. Основное уравнение термодинамики
 (1.8)
(1.8)
связываетпять функций состояния: р, Е, 5, Т и v. Если две из них выбрать в качественезависимых переменных, например Т и v, то для определения трех функций, p, Е, S, необходимы три уравнения. Отсюда следует, что уравнения (1.5) — (1.7) cовместнос (1.8) не могут быть независимы. Для нахождения связи между ними запишем дифференциалы S и Е:
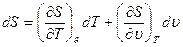 (1.9)
(1.9)
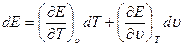 (1.10)
(1.10)
Поставим уравнение (1.10) в основное уравнение термодинамики (1.8):
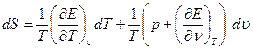 (1.11)
(1.11)
Сравнивания уравнения (1.9) и (1.10) получим:
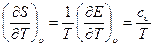
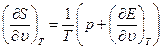 (1.12)
(1.12)
Дифференцированием этих уравнений можно исключить S:
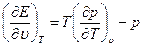 (1.13)
(1.13)
Уравнения (1.12) показывают, что если известны уравнения состояния (1.5) и (1.6), то можно определить уравнение (1.7) с точностью до произвольной постоянной. При этом уравнения (1.5) и (1.6) связаны между собой дифференциальным соотношением (1.12). Если известно только уравнение (1.5), то с помощью уравнения (1.13) можно получить Е с точностью до произвольной функции Т.
|
|
|
Среди пяти термодинамических функций, р, 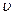 , T, Е, S, можно выбрать любые две в качестве независимых переменных.
, T, Е, S, можно выбрать любые две в качестве независимых переменных.
если в качестве независимых переменных принять удельный объем v и энтропию S, то, используя уравнение (1.8) и дифференциал для Е = Е (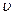 ,S), получим
,S), получим
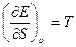
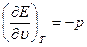 (1.14)
(1.14)
Исключая из этих уравнений Е с помощью дифференцирования, получим
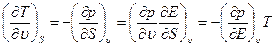 (1.15)
(1.15)
если уравнения состояния имеют вид
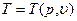
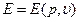
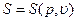
то, на основании термодинамического уравнения (1.8), существуют следующие уравнения, которые связывают Е, S и Т:

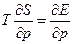 (1.16)
(1.16)
Исключая отсюда Т, получим
 (1.17)
(1.17)
Если известно уравнение состояния 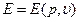 , то можно получить уравнение состояния
, то можно получить уравнение состояния  с точностью до произвольной функции энтропии S. Исключая из (1.16) Е, получим
с точностью до произвольной функции энтропии S. Исключая из (1.16) Е, получим
 (1.18)
(1.18)
При известном уравнении состояния 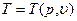 из этого уравнения можно получить уравнение состояния
из этого уравнения можно получить уравнение состояния  с точностью до произвольной функции энтропии S.
с точностью до произвольной функции энтропии S.
Если уравнение состояния известно в виде 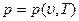 , то можно определить уравнение состояния
, то можно определить уравнение состояния
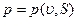 (1.19)
(1.19)
Для этого, считая, что 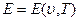 , запишем выражение
, запишем выражение
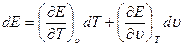
Используя (1.8) и (1.13), а также учитывая, что 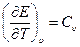 , получим
, получим
 (1.20)
(1.20)
Отсюда

Интегрируя это уравнение, получим
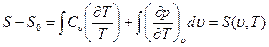 (1.21)
(1.21)
 Если исключить отсюда Т с помощью известного уравнения
Если исключить отсюда Т с помощью известного уравнения 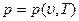 , то можно получить уравнение состояния (1.19). Так, например, если уравнение
, то можно получить уравнение состояния (1.19). Так, например, если уравнение 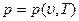 имеет вид
имеет вид
 (1.22)
(1.22)
то 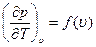 ). Если принять, что
). Если принять, что 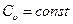 , уравнение (1.21) примет вид
, уравнение (1.21) примет вид
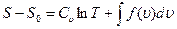 (1.23)
(1.23)
Определим Т из уравнения (1.22) и подставим его в уравнение (1.23); в результате получим
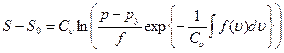 (1.24)
(1.24)
или
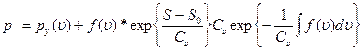 (1.25)
(1.25)
Это и есть искомое уравнение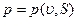 , соответствующее уравнению состояния
, соответствующее уравнению состояния  .
.
Для совершенного газа уравнение состояния имеет вид 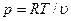 . Подставляя это уравнение в (1.23), получим уравнение состояния в виде
. Подставляя это уравнение в (1.23), получим уравнение состояния в виде
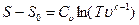 ,
,
или
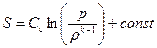 . (1.26)
. (1.26)
Уравнения (1.24) и (1.26) при условии S = const являются уравнениями изоэнтропы. Для совершенного газа уравнение изоэнтропы имеет вид 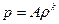 , где А = const.
, где А = const.
Если уравнение 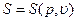 имеет вид (1.24), то условие адиабатности движения среды будет
имеет вид (1.24), то условие адиабатности движения среды будет
|
|
|
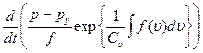 (1.27)
(1.27)
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 310; Нарушение авторских прав?; Мы поможем в написании вашей работы!