Дисперсия процесса изнашивания

Стохастическая природа изнашивания.

g - скорость изнашивания материала

k – const, зависящая от материала и условий изнашивания (смазка, вакуум).

Р – давление на поверхность трения

V – скорость скольжения

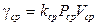
A (t) – случайная величина

j(t) – неслучайная величина

,

где 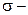среднеквадратическое отклонение

Дисперсия процесса изнашивания может быть подсчитана на основании теории о дисперсии независимых, не центрированных случайных величин.

ГЛАВА 3.

Модели формирования отказов.

§1.Модель формирования постепенного отказа.

;

где X – толщина изношенного слоя, мкм; g - скорость изнашивания, мкм/час; t – время работы механизма, час

Скорость изнашивания подчиняется нормальному закону:

;

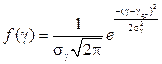где 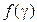– плотность вероятности; – среднее значение (мат. ожидание) скорости изнашивания; – среднеквадратическое отклонение скорости изнашивания.

Предельно допустимое значение толщины изношенного слоя X_max установлено из условия правильности функционирования изделия.

При Х = Х_max наступает предельное состояние, которое и определяет срок службы (наработку) изделия до отказа. Это наступает в момент времени t = T (срок службы).

Срок службы Т является функцией случайного аргумента g, т.е.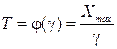

Средний срок службы изделия:

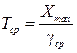
Задача заключается в отыскании плотности распределения по заданной плотности распределения .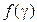

Для функции случайного аргумента в теории вероятности применяется формула:

где y(T) – функция, обратная функции j(g), т.е. если , то

,

;

;

;

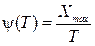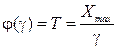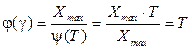Итак,

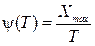
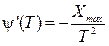
где – коэффициент вариации, величина безразмерная

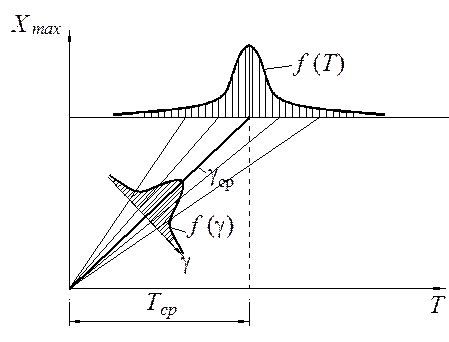
Для удобства расчётов введём безразмерное время

, тогда

;

Для определения вероятности отказа F (T) необходимо проинтегрировать функцию плотности вероятности

Если ввести переменную , данный интеграл сводится к функции Лапласа и, учитывая что вероятность безотказной работы , получим

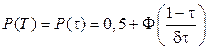
Зная, что и 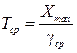, получим

Подсчитаем вероятность F(g):

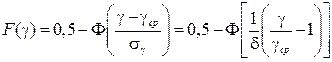
Из выражени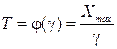й и получаем .

Тогда

Т.е. 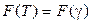или

Параметр Х при заданном Т, так же как и скорость g, распределен по нормальному закону с параметрами:

Поэтому вероятность безотказной работы численно равна площади под кривой плотности распределения f (X), заключённая от -¥ до X_max:

§2. Модель формирования постепенного отказа

с учётом рассеивания начальных параметров.

Более полная схема потери изделием работоспособности учитывает начальное рассеивание параметров изделия.

,

где а – начальный параметр изделия, например, начальный зазор.

Срок службы изделия является функцией двух независимых случайных аргументов a и g.

;

;

;

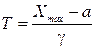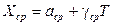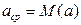
где 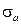– среднеквадратическое отклонение случайного параметра

Применяя условие, что 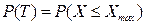получаем:

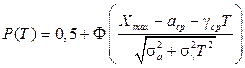
При 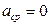имеем

При 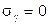имеем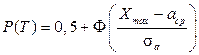

Последняя формула от времени 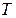не зависит, т.е. это случай, когда

Пусть имеем X_max и X _min

Если , a g _ср = 0, то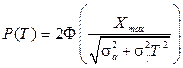

§3. Модели внезапных отказов.

Вероятность события В при условии выполнения события А: означает условную вероятность безотказной работы изделия за период времени D t.

Применяя теорему умножения вероятностей для рассматриваемого случая, получим:

По определению, интенсивность отказов l равна:

Откуда следует

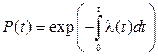
Эта формула выражает зависимость между вероятностью безотказной работы изделия и l–характеристикой, которая в общем случае может быть функцией времени l(t).

Интенсивность отказов не является самостоятельной характеристикой, так как связана с P(t) и плотностью вероятности f (t):

;

Поэтому, т.к. ;

При l = const:

,

т.е. имеет место экспоненциальный закон

Т.к. 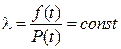, то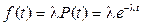

Средний срок службы (наработка) до отказа для экспоненциального закона будет:

; тогда ;

При

Т.е. при внезапных отказах после работы одинаковых деталей или узлов в течение времени 63% изделий откажут, а 37% — останутся работоспособными.

Для современных деталей и узлов машин требуется высокая вероятность безотказной работы:

P (t)=0,99 0,9999;

Для значений P (t) > 0,9

ГЛАВА 4.

Надёжность в период постепенных отказов.

§1.Нормальное распределение.

Для постепенных отказов нужны законы распределения времени безотказной работы, которые дают в начале низкую плотность распределения, затем максимум и далее падение, связанное с уменьшением числа работоспособных элементов.

Нормальное распределение является наиболее универсальным, удобным и широко применяемым для практических расчётов.

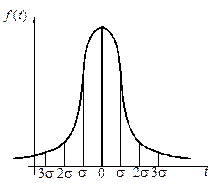
Нормальному распределению подчиняется наработка до отказа многих восстанавливаемых и невосстанавливаемых изделий, размеры и ошибки измерения деталей и т.д.

Плотность распределения:

Распределение содержит два независимых параметра:

– математическое ожидание

s - среднеквадратическое отклонение

Значения этих параметров оцениваются по результатам испытаний:

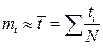
, s^* - оценки математического ожидания и среднеквадратического отклонения.

Функция распределения:

Вероятность отказа и вероятность безотказной работы соответственно равны:

; ;

;

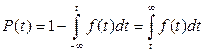
Вычисление интегралов заменяют использованием таблиц. Для использования таблиц применяют следующую подстановку:

х – квантиль нормированного нормального распределения. Величину X обозначаем u_p.

Часто в литературе по теории надёжности вместо интегральной функции распределения F (x) используют функцию Лапласа:

Очевидно, что

Вероятность отказа и вероятность безотказной работы, выраженные через функцию Лапласа, отличаются пределами интегрирования:

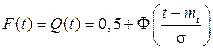
Помимо задачи оценки вероятности безотказной работы за данное время или за данную наработку встречается обратная задача: определение времени или наработки, соответствующих заданной вероятности безотказной работы.

Значение этой наработки (времени) определяют с помощью квантилей нормированного нормального распределения.

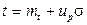
Отношение 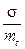называют коэффициентом вариации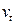

ЗАДАЧА 1

Оценить вероятность безотказной работы в течение времени часов изношенного подвижного сопряжения, если ресурс по износу подчиняется нормальному распределению, часов и s = 10 часов.

РЕШЕНИЕ:

Находим квантиль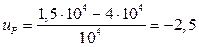

По таблице квантилей определяем нормальное распределение P (t) = 0,9938.

ЗАДАЧА 2

Оценить 80% ресурса ТО, если известно, что его долговечность ограничена по износу, ресурс подчиняется нормальному распределению с параметрами: 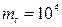часов,

часа.

РЕШЕНИЕ:

при P (t) = 0,8 по таблице находим = - 0,84 и

часа

§2 Усечённое нормальное распределение.

Получается из нормального при ограничении интервала изменения случайной величины при том условии, что площадь под кривой должна оставаться равной единице. При этом график нормального распределения «приподнимается»:

Плотность распределения записывается также, как и плотность нормального распределения, но с коэффициентом пропорциональности С:

где значение случайной величины, соответствующей максимуму f (t) и называемое модой.

Коэффициент С для распределения, ограниченного пределами изменения от a до b определяется из условия:

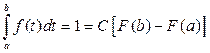
где 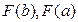– значения функции нормального распределения для предельных значений t. Отсюда

§3.Логарифмические нормальные распределения.

Логарифм случайной величины распределяется по нормальному закону. Как распределение положительных величин, оно несколько точнее, чем нормальное, описывает наработку до отказа деталей, в частности, по усталости. Его успешно применяют для описания наработки подшипников качения, электронных ламп и других изделий.

Плотность распределения описывается зависимостью

где m и s - параметры, оцениваемые по результатам испытания.

При испытаниях N изделий до отказа

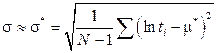
где m^*,s^* - оценка параметров m и s.

Вероятность безотказной работы можно определить по таблицам для нормального распределения в зависимости от значения квантили.

Математическое ожидание наработки до отказа:

Среднеквадратическое отклонение:

;

Коэффициент вариации:

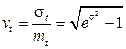
Часто применяют запись зависимости для логарифмического нормального распределения в десятичных логарифмах.

Соответственно плотность распределения:

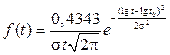
Оценки параметров и s определяются по результатам испытаний.

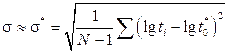
где и — оценки параметров и.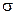

Математическое ожидание , среднеквадратическое отклонение 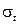и коэффициент вариации 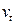наработки до отказа соответственно равны:

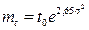
§4. Математические ожидания, мода и

медиана непрерывной случайной величины.

Математическое ожидание (m) непрерывной случайной величины – это абсцисса центра тяжести фигуры, расположенной под кривой распределения.

Мода непрерывной случайной величины (M) – это наиболее вероятное значение случайной величины или max кривой распределения.

Медиана непр=ерывной случайной величины (Me) – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам.

Примечание:

В случае симметрии нормального распределения медиана совпадает с модой и математическим ожиданием.

ГЛАВА 5.

Резервирование как метод повышения надёжности

§1. Надёжность сложных систем.

Под элементом будем понимать составную часть сложной системы, которая может характеризоваться самостоятельными входными и выходными параметрами.

Двухступенчатый зубчатый редуктор.

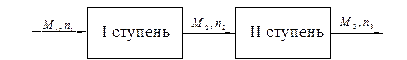
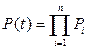
Если причина выхода из строя элемента т.о. связана только с внезапными отказами, которые подчинены экспоненциальному закону, то:

;

,

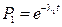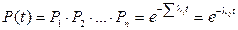где .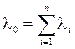

§2. Резервирование ненадёжных элементов.

Для повышения надёжности сложных систем можно применять резервирование, т.е. создавать дублирующие элементы.

При выходе из строя одного из элементов, дублёр выполняет его функции, элемент, таким образом не прекращает работу.

При постоянно нагруженном резерве резервные элементы находятся в одинаковом режиме работы с основным элементом.

Схема расчета вероятности безотказной работы

Пусть – вероятность появления отказа каждого из элементов за время T.

Отказ всей системы – сложное событие, которое будет иметь место при условии отказа всех элементов системы.

Вероятность совместного появления всех отказов F (t) по теореме умножения вероятностей будет:

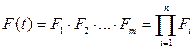
Тогда вероятность безотказной работы всей системы с параллельно резервированными элементами будет равна:

P (t)=1-(1-0,9)²=1-0,01=0,99

При m =2 P (t)=0,99

m =3 P (t)=0,999

m =4 P (t)=0,9999

Возможно создание ненагруженного резервирования (резервирования замещением), когда резервные цепи находятся в отключенном состоянии и включаются лишь в том случае, если основной элемент отказывает.

Для нагруженного резерва надёжность резервных элементов не зависит от того, в какой момент времени они включились на место основного.

Ненагруженные резервные элементы не работают до момента их включения вместо основного элемента. В этот период их отказ невозможен.

§3. Задача о расчёте надёжности элемента с

восстановлением (задача Гнеденко Б.В.).

При отказе основного элемента его замещает резервный, а основной элемент начинает восстанавливаться (ремонтируется или заменяется), после чего становится в резерв.

Отказ пары (элемента и дублёра) наступит тогда, когда на каком-либо цикле, во время восстановления одного элемента, отказывает другой.

Пусть l - интенсивность отказа основного элемента, а l _p – интенсивность отказа резервного элемента и G (t) – закон распределения времени ремонта.

При малой вероятности отказа пары на одном цикле, вероятность безотказной работы всей системы может быть выражена приближенной формулой:

,

где – математическое ожидание времени ремонта.

§4. Резервирование систем.

Резервирование бывает общим или раздельным.

Общее резервирование означает, что при выходе из строя любого элемента, включается резервная цепь, которая полностью заменяет данную.

Раздельное резервирование обеспечивает возможность включения резервного элемента при выходе из строя любого элемента системы.

Рассмотрим более подробно две эти схемы.

Общее резервирование.

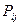– вероятность безотказной работы одного элемента

Первая цепь 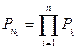; вторая цепь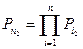

Вероятность безотказной работы всей системы:

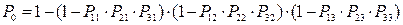
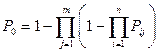
Раздельное резервирование.

Та же цепь, но каждый элемент имеет свой резерв.

Это резервирование является наиболее эффективным.

В соответствии с государственными стандартами показатели системы нормируются.

Класс надёжности
P (t)	<0,19	³0,19	³0,99	³0,999	³0,9999	»1

§5. Примеры расчёта надёжности с резервированием и без.

Пример1. Определение вероятности безотказной работы привода, состоящего из электродвигателя, упругой муфты и двухступенчатого зубчатого редуктора.

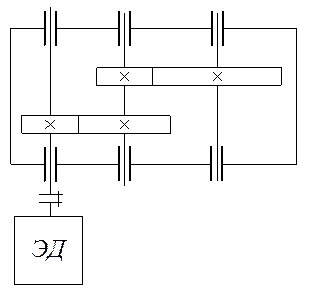
Дано:

P ₁ = 0,99 – вероятность безотказной работы ЭД

P ₂=0,9973 – вероятность безотказной работы муфты

P _3,6,9 = 0,999 - вероятность безотказной работы валов

Р _4,7,10 = 0,99 - вероятность безотказной работы подшипников

Р _5,8 = 0,9973 - вероятность безотказной работы зубчатых передач

Р_М = 0,9999 - вероятность безотказной работы масла

Расчёт: составляем структурную схему вероятностного расчёта

Пример 2. Определение вероятности безотказной работы привода, состоящего из электродвигателя, упругой муфты, двухступенчатого зубчатого редуктора, выполненного по соосной схеме с резервированием на полную мощность. Исходные данные применяются как в примере 1.

Расчёт: составляем структурную схему вероятностного расчёта.

Примечание: Несмотря на то, что надёжность привода с резервированием выше на 5,5%, чем без резервирования, она так же невелика, что является следствием увеличения числа подшипников, вероятность безотказной работы которых принята весьма низкой из-за отсутствия методов расчёта на вероятность, большую чем 0,99.

ГЛАВА 6.

Диагностика технических объектов.

§1. Задачи технической диагностики.

Весьма важно иметь методы и средства для оценки технического состояния объекта, т.е. определения степени удалённости оценки от предельного состояния, выявления причин нарушения работоспособности, установления вида и места возникновения повреждения и т.п.

Все эти задачи решаются методами диагностирования, применение которых позволяет получить большой экономический эффект за счёт более полного использования потенциальных возможностей т.о.

Результаты диагностирования могут быть использованы для прогнозирования надёжности объекта и для принятия решения о проведении ремонта.

Диагностические признаки:

1. Контролируются выходные параметры изделия или его узлов.

2. Контролируются повреждения, которые приводят, или могут привести к отказу изделия.

Величины износа, деформации, вакуум являются теми диагностическими признаками, по которым можно сделать вывод о техническом состоянии объекта.

В общем случае должен быть осуществлён поиск неисправностей, например методом последовательных разбиений всего множества элементов на две части.

Неисправную часть снова разбивают на две и продолжают анализ до тех пор, пока не будет обнаружено место повреждения.

3. Контроль работоспособности изделия по косвенным признакам производится в том случае, когда непосредственно измерение выходных параметров затруднено.

Косвенными диагностическими признаками могут служить: изменения температуры, наличие в смазке продуктов износа.

§2.Диагностирование сложных систем.

Для диагностической модели входным параметром X будет значение показателя качества изделия, а входным параметром некоторый диагностический параметр – диагностический сигнал .

В общем случае в векторной форме можно записать

,

где A -оператор, характеризующий те преобразования, которые необходимо осуществить с величиной Х, чтобы получить S.

По совокупности значений множества параметров судят о принадлежности объекта к тому или иному классу:

1 класс: объект работоспособен

2 класс: объект работоспособен, но требует подналадки.

3 класс: объект неработоспособен и требует ремонта.

§3. Структура системы диагностирования.

В общем виде можно представить следующую структурную схему диагностики технических элементов:

Датчики (преобразователи), установленные на объекте диагностирования, передают разнообразные сигналы, которые преобразуются в электрические величины и поступают в блок обработки информации и оценки состояния изделия или характера изменения его параметров.

Для всех сигналов, с которыми необходимо сравнивать поступающие диагностические сигналы, предусматривается массив допустимых эталонных значений.

В некоторых случаях, чтобы оценить техническое состояние объекта, на него подаются специальные тестовые воздействия для оценки реакции объекта диагностики.

Для повышения достоверности получаемых данных осуществляется самоконтроль путем повторного выполнения отдельных операций (повторная диагностика) и сравнение полученных данных.

§4. Диагностика технологических устройств

на основе применения формулы Байеса.

Задача ставится следующим образом: известны состояния системы, включающие нормальные и типовые состояния неисправностей и их вероятностей.

Произведены наблюдения в эксплуатации или испытания, в результате чего зафиксированы некоторые признаки.

Спрашивается, как в связи с этим изменятся (уточняться) вероятности состояния системы?

Признаки:

— нагрев

— увеличение времени разгона

— увеличение погрешности изделий (позиционирования).

Для анализа необходимы статистические сведения о частости наблюдения отдельных признаков при каждом типовом состоянии системы. Эти частости в дальнейшем рассматриваются как вероятности.

Вероятность сложного события возникновения состояния и проявления комплекса 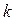признаков , согласно теореме умножения вероятностей:

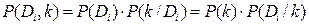
– априорная (известная) вероятность состояния D_i;

P (k / D_i) – условная вероятность возникновения комплекса признаков k;

P (k) – полная вероятность возникновения комплекса признаков в системе;

P (D_i / k) – условная вероятность состояния D_i при комплексе признаков k;

Отсюда, отбрасывая левую часть, получаем:

Состояние образуют полную группу несовместных событий, т.е. событий, из которых реализуется только одно.

Полная вероятность появления комплекса признаков k в системе равна сумме вероятностей появления этого комплекса признаков при отдельных состояниях.

Подставляя, получим формулу Байеса для вероятности некоторого состояния D_i при комплексе признаков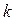

Комплекс признаков 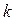рассматривается состоящим из признаков , которые полагаются независимыми.

Тогда вероятность 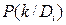рассматривается как вероятность сложного события, равная произведению вероятностей простых событий:

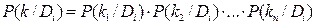
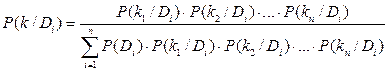
Если некоторые признаки являются зависимыми, то формула трансформируется. Например, если для состояния зависимыми являются признак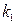и и , то в формулу вместо произведения подставляют

.

При использовании формулы, отсутствие какого-либо признака, например, 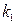, рассматривается как противоположное событие с вероятностью .

Если существует признак , встречающийся только при одном состоянии системы и не встречающийся при других, то он называется детерминированным.

Из предыдущей формулы следует то, что при i =m P (D_i / k)=1, а при i ¹m P (D_i / k)=0

Пример 1:

Для обследуемого оборудование характерно три состояния:

- состояние D ₁ – неисправности узла 1, наблюдаемые у 5% оборудования, т.е. P (D ₁)=0,05;

- состояние D ₂ – неисправности узла 2, наблюдаемые у 15% оборудования, т.е. P (D ₂)=0,15;

- нормальное состояние D3 – наблюдаемое у 80% оборудования, т.е. P (D ₃)=0,8.

- Признак 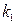наблюдается при состоянии D ₁ в 20% случаев. Отсюда следует:

P (k ₁/ D ₁)=0,2; при состоянии D ₂ в 40% будет P (k ₁/ D ₂)=0,4 и при нормальном состоянии не наблюдается.

- Признак k ₂ наблюдается при состоянии D ₁ в 30% случаев, ; при состоянии в 50% случаев, 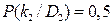; и при нормальном состоянии в 8% случаев,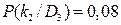

Дата добавления: 2014-01-11