Основные понятия и простейшие свойства рядов

Теоретическая часть

Интернет-ресурсы

1. www.exponenta.ru

Тема 1. Числовые ряды и их приложения.

Определение: Пусть имеется бесконечная последовательность чисел 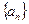, 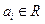. Сумма 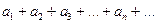в сокращенной записи 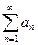(1) называется числовым рядом.

Примеры:

1. Выписать первые 4 члена ряда:

=

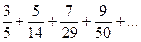
2. Подобрать один из возможных вариантов формулы общего члена ряда:

Числители дробей являются первыми четными числами: 2,4,6,8…

Можно предположить, что числитель дроби, соответствующий k-му члену данного ряда, будет k-е по счету четное число: 2k.

Знаменатели дробей являются первыми четырьмя членами арифметической прогрессии с разностью, равной 3, и первым членом равным 5.

Это возможный вариант, но не единственный.

Числа называются членами ряда.

Выражения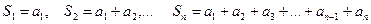

называются частичными суммами ряда (1). Частичные суммы образуют числовую последовательность.

Определение. Если существует конечный предел последовательности n-х частичных сумм , (2)

то он называется суммой ряда (1).

Если S, конечное число, то ряд называется сходящимся. Если же предел (2) бесконечен или не существует, то ряд называется расходящимся.

В качестве примера рассмотрим сумму бесконечной геометрической прогрессии

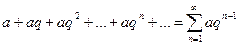
Из элементарной математики известна формула суммы n членов прогрессии (n-ая частичная сумма в нашей терминологии), полученная в предположении, что .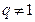

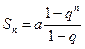
Если 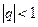, то и ряд будет сходящимся.

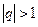Если , то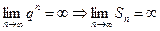, соответственно ряд будет расходящимся.

Если 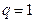, то .

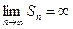Наконец, если 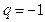, то частичная сумма с четного числа слагаемых

,

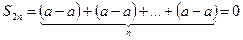а частичная сумма нечетного числа слагаемых будет равна . Последовательность таких частичных сумм предела не имеет и ряд в этом случае также расходящийся.

Примеры:

Найти сумму ряда:

1.

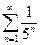
Данный ряд представляет собой сумму бесконечно убывающей геометрической прогрессии с первым членом 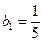и знаменателем , а значит, сумму его можно найти по формуле суммы бесконечно убывающей геометрической прогрессии

.

2.

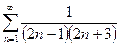
Разложим общий член ряда на простые дроби:

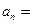
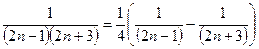, (можно воспользоваться методом неопределенных коэффициентов), вычислим n-ю частичную сумму ряда: 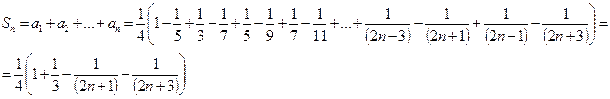тогда по определению суммы ряда

.

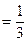3.

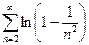
Вычислим n-ю частичную сумму ряда:

, тогда .

Дата добавления: 2014-01-11