Найбільший спільний дільник

Спільний дільник многочленів f(x) та g(x), який ділиться на кожний інший спільний дільник цих многочленів, називається їх найбільшим спільним дільником (НСД) і позначається (f, g). НСД многочленів визначається однозначно з точністю до сталого множника (оскільки, якщо d(x) – НСД, то й c·d(x), де , теж НСД).

Многочлени f(x) та g(x) називаються взаємно простими, якщо кожний їхній спільний дільник є ненульовою константою, тобто (f, g)=1.

Розглянемо спосіб знаходження НСД (алгоритм Евкліда).

Нехай дано многочлени f(x) та g(x), причому 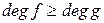. Виконаємо послідовне ділення з остачею:

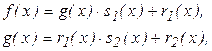
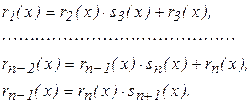
Тут 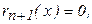оскільки послідовність степенів многочленів g(x), r₁(x), r₂(x), ... є монотонно спадною. Оскільки степінь r₁(x) не вищий за m-1, де m= deg g, то кількість кроків в алгоритмі не перевищує m.

Оскільки (f, g)=(g, r₁)=(r₁, r₂)=(r₂, r₃)=…=(r_n-1, r_n)=(r_n, 0)=r_n, що випливає із записаног вище алгоритму Евкліда. то остання відмінна від нуля остача r_n(x) в цьому алгоритмі і є НСД многочленів f(x) і g(x).

Приклад.

З допомогою алгоритму Евкліда знайти НСД многочленів

f(x)=x³–3x²+3x–1, g(x)=x³–1.

x³–3x²+3x–1=(x³–1)·1+(-3x²+3x)

x³–1=(-3x²+3x)·()+(x–1)

-3x²+3x=(x–1)·(-3x).

Отже, (f,g)=x–1.

НСД більшої кількості многочленів, зокрема, f₁(x), f₂(x), …, f_n(x) шукають так:

d₁(x)=(f₁, f₂), d₂(x)=(d₁, f₃), d₃(x)=(d₂, f₄), …, d_n-1(x)=(d_n-2, f_n).

d_n-1(x) і є НСД многочленів f₁(x), f₂(x), …, f_n(x).

Якщо хоча б два многочлени із системи f₁(x), f₂(x), …, f_n(x) взаємно прості, то НСД усіх цих многочленів дорівнює одиниці.

Якщо позначити d(x)=r_n(x), то, піднімаючись вгору рівностями алгоритму Евкліда, можна отримати вираз

d(x)=f(x)·u(x)+g(x)·v(x),

тобто 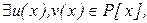такі що (f, g) виражається через f(x) і g(x).

Дата добавления: 2014-01-11