Обобщенное распределение Эрланга

Обычно распределение Эрланга используется в случаях, когда длительность какого-либо процесса можно представить как сумму к элементарных последовательных составляющих, распределенных по экспоненциальному закону. Если обозначить математическое ожидание длительности всего процесса как M[t]=1/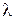, среднюю длительность элементарной составляющей как 1/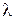, то плотность вероятностей распределения Эрланга представляется следующей формулой:

Дисперсия такого распределения D[t]=

Очевидно, что при к=1 - это экспоненциальное распределение. Разновидности этого распределения для разных к>0 представлены на рис. 9.4. Предположим, что в распределении Эрланга имеется не строго фиксированное число экспоненциально распределенных отрезков к, а переменное, с вероятными изменениями в пределах одного интервала. Тогда можно говорить лишь о средней величине s таких отрезков, где s - число с плавающей точкой. После такого перехода от дискретных к непрерывным величинам появляется возможность работы и со значениями в пределах 0<s<1.

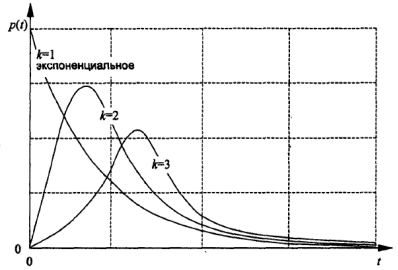
Рис. 1.5. Вид распределения Эрланга при различных значениях к:

1 - экспоненциальное; 2,3 - распределения второго и третьего порядков

Рассмотрим программную функцию, реализующую такое распределение

f l o a t erlang{float m, float s)

{

f l o a t a, b;

i n t i, k;

a = 0.0;

к = Sj to

= S - k;

for(i=0;i<k;i++)

a += expont(m);

if (rundumO < b)

a += expont(m);

return(a);

}

Эта функция имеет два входных параметра:

• m - математическое ожидание элементарного интервала времени, причем m=1/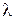k,

• s - среднее число элементарных отрезков в общей длительности процесса.

Видно, что при значениях s 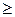1 (в том числе целых) получаем обычное распределение Эрланга с параметрами: M[t\ = ms = 1/ 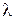и D[t] – m²s= . Однако при 0<s<0 это распределение меняется коренным образом: фактически мы получаем процесс испытаний Бернулли. В результате этих испытаний «успехом» считается получение элементарного отрезка, распределенного по экспоненциальному закону с математическим ожиданием m (вероятность успеха равна s), а неудачей с вероятностью 1- s является получение элементарного отрезка с нулевой длиной. Если по такому правилу будет работать какой-то генератор заявок, то он будет создавать группы заявок. Причем средний размер группы будет равен n = 1/s, а средний интервал времени между двумя последовательными группами равен m.

Математическое ожидание интервала между двумя последовательными заявками и в этом случае определяется выражением M[t] = ms = 1/ 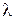. Что касается дисперсии, то она существенно меняется и определяется по формуле:

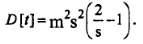
Одно из свойств групповых потоков заключается в том, что среднеквадратичное отклонение интервала между заявками превосходит математическое ожидание этого интервала.

Если имеется возможность собрать статистику по групповому потоку на практике или получить такой поток с помощью рассмотренной выше программной функции, то можно определить коэффициент вариации с и связь этого коэффициента со средним размером группы заявок по формуле

Это соотношение позволяет отслеживать появление групповых потоков в реальных системах или в их имитационных моделях.

Обобщенное распределение Эрланга применяется при создании как чисто математических, так и имитационных моделей в двух случаях. Во-первых, его удобно применять вместо нормального распределения, если модель можно свести к чисто математической задаче, применяя аппарат марковских или полумарковских процессов либо используя метод Кендалла. Однако такие модели далеко не всегда адекватны реальным процессам. Во-вторых, в реальной жизни существует объективная вероятность возникновения групп заявок в качестве реакции на какие-то действия, поэтому возникают групповые потоки. Применение чисто математических методов для исследования в моделях эффектов от таких групповых потоков либо невозможно из-за отсутствия способа получения аналитического выражения, либо затруднено, так как аналитические выражения содержат большую систематическую погрешность из-за многочисленных допущений, благодаря которым исследователь смог получить эти выражения. Для описания одной из разновидностей группового потока можно применить обобщенное распределение Эрланга, которое рассмотрим ниже. Внешне похожее на гамма-распределение, оно имеет свои математические особенности.

Появление групповых потоков в сложных экономических системах приводит к резкому увеличению средних длительностей различных задержек (заказов в очередях, задержек платежей и др.), а также к увеличению вероятностей рисковых событий или страховых случаев.

Дата добавления: 2014-01-11