A solution of linear homogeneous differential equations of the second order with constant coefficients

Proof.

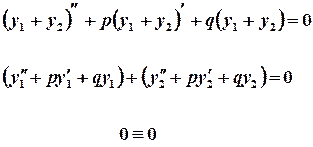
A function is a solution of equation.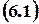

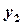Theorem 6.3. Let functions and be the linear dependent solutions of equation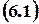, then will be not the general solution of equation.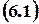

Proof. Because and 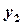are the linear dependent, then

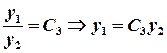
Substitute 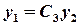into , we get

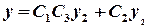
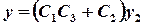, denote,

.

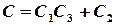The solution can not be general solution of equation 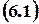, because the solution of any differential equation of the second order must have two arbitrary constants.

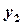Theorem 6.4.. Let functions and be the linear independent solutions of equation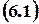, then will be the general solution of equation.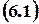

Proof. Because and 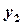are solutions of equation 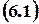, according to the

Theorem 6.1, 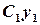and 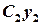also will be the solutions of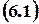. Their sum, due to Theorem 6.2,will be the solution of.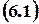

Conclusion. To find the general solution of equation 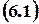it is necessary to find two linear independent solutions of 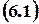and write the general solutions in the form, where and are arbitrary constants.

For finding particular solution we need to find two constants. For that we will use initial conditions:

.

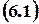
A solution of this equation we will find in the form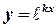, where 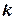is unknown constant.

Finding , 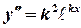and substituting into equation 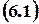, we will have

Because, then

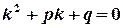
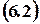
Definition 6.3. An equation 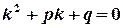is called the characteristic equation of the differential equation.

If 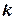is the solution of equation 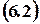, then 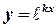also will be the solution of 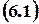. The form of solution of differential equation 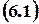will depend on the solution of equation.

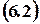Let us consider three cases:

I. , then the general solution of differential equation 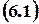will be

.

In fact, if are roots of the equation 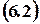, then 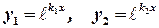are roots of equation 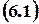. In example 6.1. we proved that 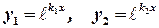are linear independent, so according to Theorem 6.4is general solution of differential equation .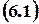

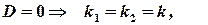
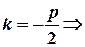
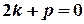
II. 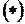, then the general solution of the differential equation 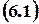will be

Дата добавления: 2014-01-11