Сегменте , а значения этой функции на концах сегмента равны и , соответственно. Тогда

Док-во. Вычислим левую и правую части данного равенства с использованием формулы Ньютона-Лейбница: левая часть ;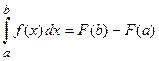

правая часть .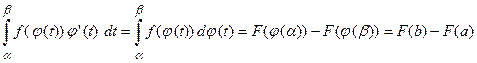

З2. Отметим, что при использовании метода замены переменной интегрирования в определенном интеграле, надо обязательно пересчитывать пределы интегрирования.

Пример 3. Вычислить .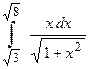

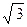
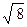
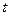
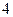
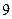
Воспользуемся методом замены переменной интегрирования в определенном интеграле, получим 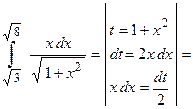(пересчитаем пределы интегрирования по формуле замены :

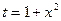получим).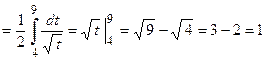

З3. При использовании метода замены переменной интегрирования в определенном интеграле после нахождения первообразной с новой переменной интегрирования не надо возвращаться к старой переменной интегрирования, а надо воспользоваться формулой Ньютона-Лейбница.

5. Интегрирование по частям в определенном интеграле.

Метод интегрирования по частям в определенном интеграле основан на формуле: .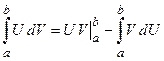

З4. При использовании метода интегрирования по частям в определенном интеграле к проинтегрированной части применяется формула Ньютона-Лейбница.

Пример 4. Вычислить .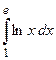

К интегралам такого вида применяется метод интегрирования по частям

.

6. Определенный интеграл от четной и нечетной функций

по симметричному интервалу интегрирования.

Пусть функция 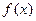является нечетной функцией, т.е. 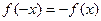, тогда

.

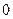
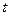
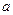
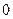
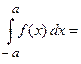
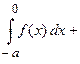
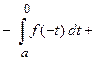
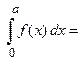
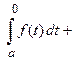
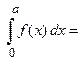
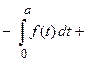
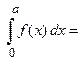
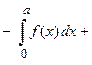
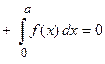Вывод: Определенный интеграл от нечетной функции по симметричному интервалу интегрирования равен нулю.

Пусть функция 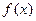является четной функцией, т.е. 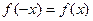, тогда

.

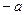
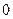
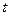
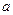
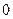
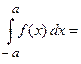
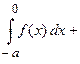
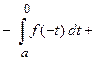
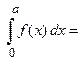
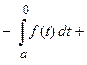
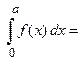
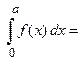
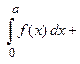
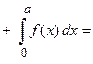
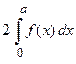Вывод: Определенный интеграл от четной функции по симметричному интервалу интегрирования равен удвоенному значению определенного интеграла по половине симметричного интервала интегрирования.

Пример 5. Вычислить .

В силу того, что подинтегральная функция является четной, то

.

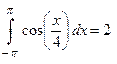
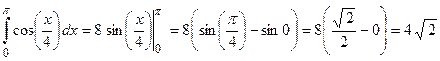Пример 6. Вычислить .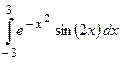

Так как подинтегральная функция нечетная, то .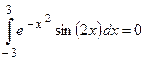

Лекция № 9 “Геометрические приложения

определенного интеграла”

1. Площадь плоской фигуры.

1. Пусть функция 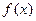непрерывна на сегменте 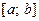и принимает на этом отрезке только неотрицательные значения (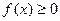), тогда согласно геометрическому смыслу определенный интеграл от этой функции в пределах от до будет равен площади криволинейной трапеции .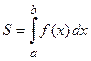

Пример 1. Вычислить площадь плоской фигуры, ограниченной линиям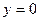и и .

Первая линия 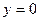определяет прямую, которая является осью абсцисс, а вторая линия определяет параболу с ветвями, направленными вниз, и поднятую ввех по оси ординат на 4 единицы. Парабола пересекает ось абсцисс в точках (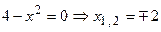) и 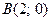(Рис. 8):

.

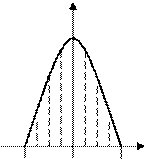
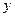
Рис. 8. Площадь плоской фигуры, ограниченной

линиям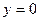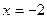и , , и .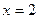

–2 2

Следовательно, 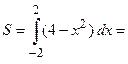(подинтегральная функция четная, а пределы интегрирования симметричные, поэтому)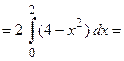

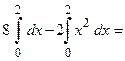
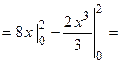
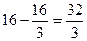. Отсюда площадь плоской фигуры .

2. Пусть функция 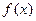непрерывна на сегменте 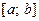и принимает на этом отрезке только неположительные значения (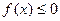), тогдаплощадь плоской фигуры может быть вычислена по одной из формул:

; ; .

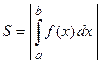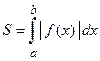Для практических расчетов предпочтительной является последняя формула.

3. Пусть функция 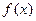непрерывна на сегменте 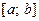и меняет на этом от-резке свой знак в точке 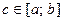, например, с “+” на “–”, тогда площадь плоской фигуры определяется формулой

Дата добавления: 2014-01-11