Группируют, например, второе и третье слагаемые уравнения

.

Т1. (о существовании и единственности решения ДУI). Если функция, стоящая в правой части ДУI, непрерывна в области, то для любых точек из области существует решение ДУI такое, что. Если при этом непрерывна частная производная, то это решение единственно.

О11. Точка, в которой нарушаются условия теоремы, называется особой.

З2. Если в области через каждую точку проходит только одна интегральная кривая, то через особую точку проходит несколько интегральных кривых.

2. ДУI с разделяющимися переменными.

О12. Дифференциальное уравнение вида 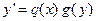называется ДУI с разделяющимися переменными.

Решение ДУI с разделяющимися переменными решают по схеме:

– обе части уравнения умножают на , при этом уравнение принимает вид ;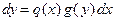

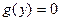– обе части уравнения делят на функцию , т.е. приводят уравнение к виду (точки, в которых определяют особые точки, при этом получаемые решения являются особыми);

О13. Дифференциальное уравнение вида 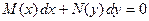называется ДУI с разделенными переменными.

– ДУI с разделенными переменными интегрируется, т.е.

З3. В общем случае ДУI с разделяющимися переменными имеет вид:

.

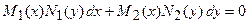Деля ДУI на произведение , получаем дифференциальное уравнение с разделенными переменными 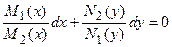. Особые решения данного ДУI следуют из решения уравнений и 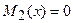. ДУI с разделенными переменными интегрируют .

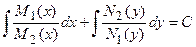Пример 3. Решить ДУI .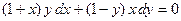

Разделим все уравнение на произведение функций 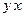(особой точкой является точка 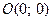), получим 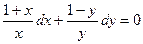. Полученное ДУ I с разделенными переменными интегрируем . Вычислим неопре-деленные интегралы, получим общее решение данного ДУ I .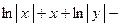

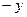
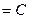Лекция № 13 “Однородные и линейные ДУ I”

1. Однородные ДУ I.

О1. Функция 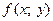называется однородной функцией 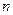-го измерения относительно переменных и 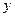, если 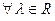имеет место равенство

.

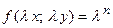
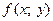Пример 1. Однородны ли функци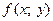и и ?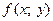

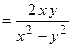Используя определение однородной функции, получаем

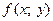
– однородная функция второго измерения;

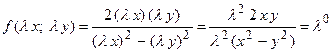
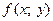
– однородная функция нулевого измерения.

Рассмотрим ДУ I , где 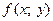– однородная функция. Выберем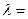 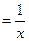, тогда дифференциальное уравнение запишется в виде

.

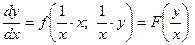З1. Если правая часть ДУ I зависит только от отношения 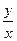, то это однородное ДУ I.

Решение однородного ДУ I проводится по схеме:

– вводят новую функцию ;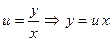

– находят производную ;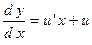

– найденные величины подставляют в однородное ДУ I ;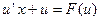

З2. В результате указанной замены однородное ДУ I сводится к ДУ I с разделяющимися переменными.

– решают ДУ I с разделяющимися переменными:

; ;

; ;

;

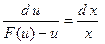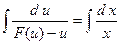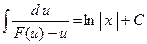– находят искомую функцию .

Пример 2. Решить ДУ I .

В правой части разделим числитель и знаменатель дроби на 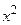, получим

уравнение , следовательно, данное дифференциальное уравнение первого порядка является однородным. Будем действовать в соответствии со схемой решения:

; ; ;;

; ; ; .

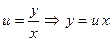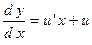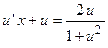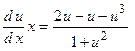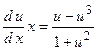Для вычисления интеграла применим метод тождественных преобразований подинтегральной функции (см. Лекцию № 2)

.

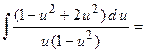
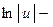
З3. Если искомая функция и ее аргумент входят в полученное общее решение дифференциального уравнения под знаком логарифма, то постоянную интегрирования рекомендуется выбирать в виде . В общем случае постоянная интегрирования выбирается из соображений упрощения формы записи общего решения дифференциального уравнения.

С учетом замечания и определения функции 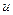получаем

; ; .

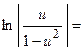
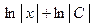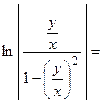
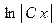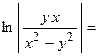
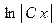Потенцируя полученное равенство и сокращая обе части равенства на , получим общее решение заданного однородного дифференциального уравнения .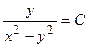

З4. Если однородное ДУ I задано в дифференциалах 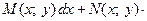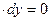, то его преобразуют к виду и решают по вышеприведенной схеме.

Пример 3. Решить ДУ I .

Приведем заданное уравнение к обычному виду 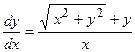. В правой части разделим числитель и знаменатель дроби на , получим уравнение , следовательно, данное дифференциальное уравнение первого порядка является однородным. Будем действовать в соответствии со схемой решения: ; ; ;; ; ; ;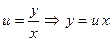

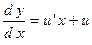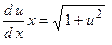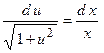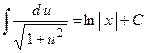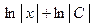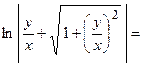
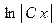. Потенцируя полученное равенство и умножая обе части равенства на , получим общее решение заданного однородного дифференциального уравнения .

2. Линейные ДУ I.

О2. Дифференциальное уравнение первого порядка вида 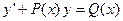называется линейным ДУ I.

Решение линейного ДУ I проводят по схеме:

– искомую функцию представляют в виде произведения двух функций, одну из которых можно выбрать произвольным образом, т.е. ;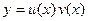

– находят ее производную ;

– найденные величины подставляют в линейное ДУ I ;

;

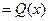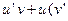
– так как одну из функци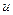й или 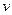можно выбрать произвольным образом, то выберем функцию 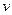так, чтобы выражение, записанное в круглых скобках обратилось в нуль, тогда уравнение будет эквивалентно системе дифференциальных уравнений первого порядка с разделяющимися пере-менными, т.е. ;

– решают первое уравнение системы (при этом постоянную интегрирования выбирают равной нулю в силу произвольности отыскиваемой функ-ции);

– найденную функцию 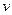подставляют во второе уравнение системы и решают его (при этом постоянная интегрирования будет произвольной и не равной нулю);

– находят искомую функцию .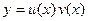

Пример 4. Решить ДУ I .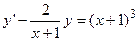

По форме записи определяем, что данное ДУ I является линейным (сравните с теоретической формой записи: 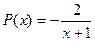; 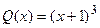). Применим вышеприведенную методику: ; ; .

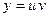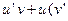
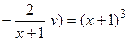Полученное уравнение эквивалентно системе дифференциальных уравнений первого порядка с разделяющимися переменными 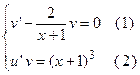. Решим первое уравнение системы

.

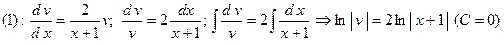Потенциируя полученное равенство, находим, что функция . Подставим эту функцию во второе уравнение системы и решим его

.

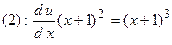Сокращая обе части равенства на 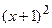и разделяя переменные, получим . Проинтегрируем полученное равенство 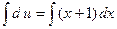, вычисляем интегралы и находим, что функция 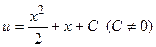. Найдем неизвестную функцию заданного ДУ I .

3. Уравнение Бернулли.

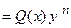
О3. Дифференциальное уравнение первого порядка вида 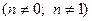называется уравнением Бернулли.

З5. При 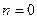уравнение Бернулли переходит в линейное ДУ I, а при 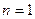– в ДУ I с разделяющимися переменными.

Разделим все уравнение на 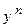, получим . Введем в рассмотрение новую функцию , тогда . Откуда находим, что величина 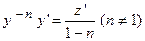. Подставим найденные величины в уравнение Бернулли 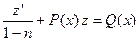, которое приводится к виду линейного дифференциального уравнения первого порядка . Следовательно, уравнение Бернулли можно решать непосредственно по схеме решения линейного ДУ I.

Пример 5. Решить ДУ I .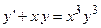

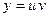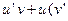
По форме записи определяем, что данное ДУ I является уравнением Бернулли (сравните с теоретической формой записи: ; ). Применим вышеприведенную методику: ; ; . По-лученное уравнение эквивалентно системе дифференциальных уравнений первого порядка с разделяющимися переменными или . Решим первое уравнение системы

.

Откуда получаем 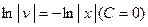. Потенциируя полученное равенство, находим, что функция . Подставим эту функцию во второе уравнение системы и решим его 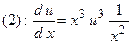. Сокращая в правой части равенства на 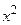и разделяя переменные, получим . Проинтегрировав полученное равенство 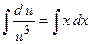, находим, что 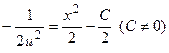. Откуда функция . Найдем неизвестную функцию заданного ДУ I .

Дата добавления: 2014-01-11