Ищется в виде суперпозиции частных решений , которые являются частными решениями уравнений

Пример 3. Решить ДУ II .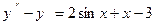

Согласно изложенной методике найдем решение однородного уравнения, которое ищем в виде 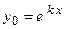, тогда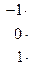

.

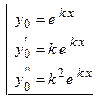
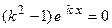Следовательно, характеристическое уравнение имеет вид 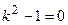. Корни уравнения в этом случае вещественные и равны 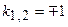, следовательно, два частных линейно-независимых решения однородного ДУ II имеют вид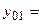 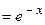и 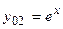. Тогда общее решение ЛОДУ II с постоянными коэффициентами в данном случае будет иметь вид: 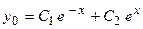. Проанализируем

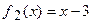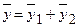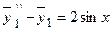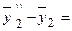
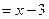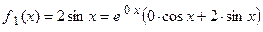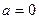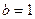правую часть данного ЛНДУ II, которая состоит из суммы двух функций, первая из которых равна , а вторая . Согласно принципу суперпозиции частных решений частное решение данного ЛНДУ II будем искать в виде , причем первое частное решение удовлетворяет уравнению , а второе частное решение – уравнению . Решим первое уравнение приведя ее правую часть к теоретическому виду: , т.е. , а . Следовательно, комплексное число 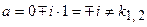, поэтому частное решение неоднородного дифференциального уравнения ищем в виде

.

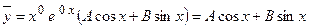Найдем первую и вторую производные этой функции и подставим найденные функции в исходное уравнение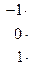

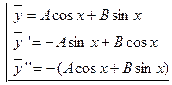
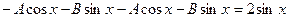
или 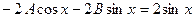. Сравнивая коэффициенты при одинаковых фун-кциях находим 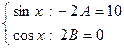. Решаем эту систему и определяем неизвестные коэффициенты: 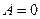, а коэффициент 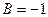. Таким образом, частное решение неоднородного ДУII имеет вид: 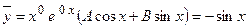. Решим второе уравнение, приведя правую часть данного ЛНДУII к теоретическому виду: 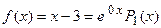. Следовательно, 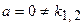, поэтому частное решение неоднородного дифференциального уравнения ищем в виде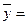 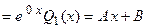. Найдем первую и вторую производные этой функции и подставим найденные функции в исходное уравнение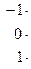

.

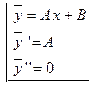
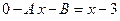Сравнивая коэффициенты при одинаковых степенях аргумента находим

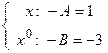. Решаем эту систему и определяем неизвестные коэффициенты: 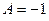, а коэффициент 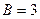. Таким образом, частное решение неоднородного ДУII имеет вид: 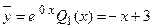. Общее решение исходного неоднородного ДУII определяется суммой всех найденных функций

.

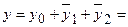
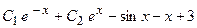Лекция № 17 “Применение ДУ II к изучению механических и электрических колебаний”

1. Колебания тела на пружине.

Пусть тело массой прикреплено к пружине с коэффициентом упругости 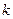, коэффициент трения о горизонтальную плоскость равен 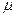. Выведем тело из положения равновесия и отпустим. На тело действуют следующие силы: сила упругости 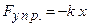, сила трения 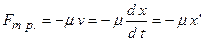и внешняя вы-нуждающая сила , которая является равнодействующей всех внешних сил, действующих на тело (Рис. 19):

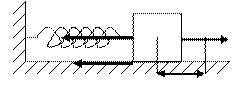
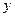
Рис. 19. Колебание тела на пружине.

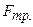
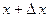
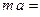
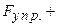
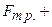
По второму закону Ньютона , где 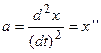– уско-рение, следовательно, уравнение движения имеет вид 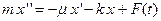. Введя обозначения 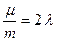, 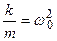и 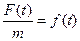, перепишем полученное уравнение в виде 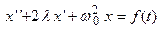. Это уравнение описывает колебания с трением под действием внешней силы. Рассмотрим частные случаи этого уравнения:

1). Пусть отсутствуют внешние силы (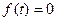) и сила трения (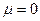), тогда уравнение принимает вид 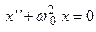и описывает свободные колебания. С математической точки зрения данное уравнение является линейным однородным дифференциальным уравнением второго порядка, поэтому ищем его решение в виде 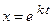. В этом случае характеристическое уравнение определяется квадратным уравнением вида , корнями которого будут величины 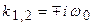. Следовательно, общее решение

.

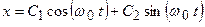Преобразуем это равенство следующим образом

.

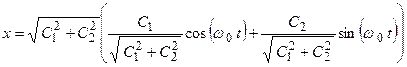Вводя обозначения 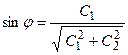, 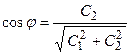и 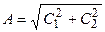, получим формулу, описывающую свободные колебания

,

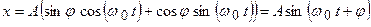где 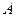– амплитуда колебаний, 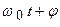– фаза колебаний, 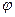– начальная фаза колебаний.

2). Пусть отсутствуют внешние силы (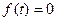), т.е. колебания осуществляются с трением (диссипативная система). В этом случае уравнение колебаний имеет вид 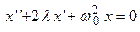, а характеристическое уравнение дается квадратным уравнением . С практической точки зрения наибольший интерес представляет случай, когда 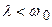. В этом случае корни характеристического уравнения равны 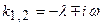, где 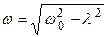. Проводя преобразования аналогичные тем, которые были проведены для предыдущего случая, запишем формулу, описывающую затухающие колебания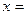 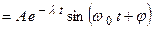. Из формулы видно, что при наличии силы трения колебания происходят с уменьшающейся амплитудой при увеличении времени .

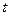3). Пусть отсутствует сила трения (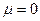), т.е. колебания осуществляются под действием внешних сил, тогда уравнение принимает вид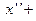 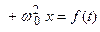. Если внешняя сила описывается периодической функцией 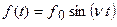, то решение ЛНДУ II представляется в виде суммы решения однородного ДУ II (см. случай 1) 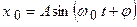и частного решения неоднородного ДУ II, которое будем искать в виде .

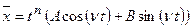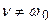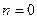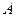а) пусть (), тогда . Подставляя эту функцию и ее вторую производную в уравнение, сравнивая коэффициенты при одинаковых функциях и решая систему линейных алгебраических уравнений относительно неизвестных коэффициентов и 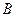, получаем, что 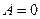, а , следовательно, общее решение имеет вид

;

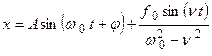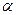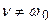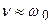) пусть , но и 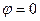, тогда решение принимает вид

;

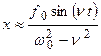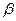) пусть 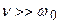и 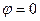, тогда .

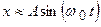б) пусть 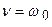(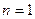), тогда 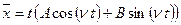. Подставляя эту функцию и ее вторую производную в уравнение, сравнивая коэффициенты при одинаковых функциях и решая систему линейных алгебраических уравнений относительно неизвестных коэффициентов 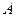и 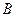, получаем, что ,

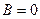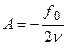, следовательно, общее решение имеет вид

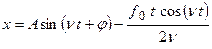
(решение дифференциальных уравнений в случаях а) и б) провести самостоятельно).

2. Колебания в электрическом контуре.

Рассмотрим следующую электрическую цепь (Рис. 20):

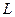
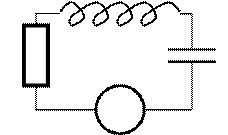
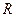
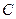Рис. 20. Электрический колебательный

контур.

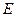
Напряжение в цепи равно

.

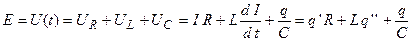Следовательно, уравнение, описывающее колебания в контуре после введения обозначени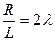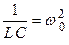й , и 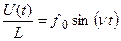, принимает вид:

.

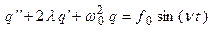Это уравнение анализируется также, как и в случае механических колебаний (исследовать полученное уравнение самостоятельно).

Дата добавления: 2014-01-11