
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Т3. Если существует предел , то радиус сходимости степенного ряда равен
|
|
|
|
Пусть на области определения все члены функционального рядаимеют непрерывные производные и ряд сходится. Если ряд, составленный из производных равномерно сходится, то исходный ряд равномерно сходится.
.
Если все члены функционального ряда непрерывны на интервале и ряд равномерно сходится, то на этом интервале функциональный ряд можно почленно интегрировать, т.е.
Пример 1. Исследовать на сходимость ряд  .
.
Данный функциональный ряд 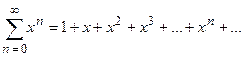 представляет собой сумму бесконечной геометрической прогрессии с первым членом
представляет собой сумму бесконечной геометрической прогрессии с первым членом 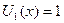 и со знаменателем
и со знаменателем 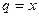 . Известно, что бесконечная геометрическая прогрессия сходится при
. Известно, что бесконечная геометрическая прогрессия сходится при 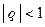 , т.е. функциональный ряд будет сходиться при
, т.е. функциональный ряд будет сходиться при  . Следовательно, функциональный ряд сходится
. Следовательно, функциональный ряд сходится 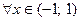 , причем равномерно, так как
, причем равномерно, так как 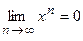 .
.
Пример 2. Вычислить сумму ряда  . Если ряд равномерно сходится, то проинтегрировать его.
. Если ряд равномерно сходится, то проинтегрировать его.
Данный ряд представляет собой сумму бесконечной геометрической прогрессии с первым членом 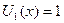 и со знаменателем
и со знаменателем  . Известно, что бесконечная геометрическая прогрессия сходится при
. Известно, что бесконечная геометрическая прогрессия сходится при 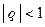 , т.е. функциональный ряд будет сходиться при
, т.е. функциональный ряд будет сходиться при 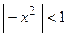 или
или  . Следовательно, функциональный ряд сходится, так как его сумма
. Следовательно, функциональный ряд сходится, так как его сумма  . Данный ряд может быть промажорирован рядом
. Данный ряд может быть промажорирован рядом  при
при 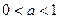 , поэтому он сходится равномерно
, поэтому он сходится равномерно 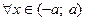 . Отсюда следует, что его можно почленно проинтегрировать на интервале от
. Отсюда следует, что его можно почленно проинтегрировать на интервале от 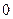 до
до  при
при 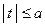 . Тогда
. Тогда 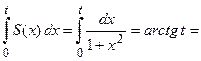
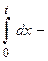

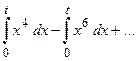
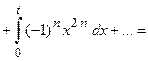
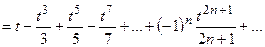 .
.
Полученное выражение представляет собой разложение функции  в ряд Маклорена, который равномерно сходится
в ряд Маклорена, который равномерно сходится  при
при 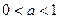 .
.
Лекция № 22 “Степенные ряды”
1. Теорема Абеля. Радиус и интервал сходимости степенного ряда.
О1. Ряд  (или ряд более общего вида
(или ряд более общего вида  , где
, где 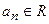 ) называется степенным рядом.
) называется степенным рядом.
Так как степенной ряд являются частным случаем функционального ряда, то он характеризуется областью сходимости, для нахождения которой применяется теорема Абеля.
|
|
|
Т1. Если степенной ряд сходится при  (
(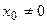 ), то он сходится абсолютно
), то он сходится абсолютно  , удовлетворяющих неравенству
, удовлетворяющих неравенству  . Если степенной ряд расходится при
. Если степенной ряд расходится при  (
(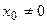 ), то он расходится абсолютно
), то он расходится абсолютно  , удовлетворяющих неравенству
, удовлетворяющих неравенству 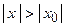 .
.
Док-во. Так как числовой ряд 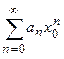 сходится, то его общий член
сходится, то его общий член 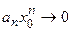 при
при 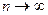 , т.е. последовательность
, т.е. последовательность  ограничена. Это означает, что существует такое положительное число
ограничена. Это означает, что существует такое положительное число  , что
, что  выполняется неравенство
выполняется неравенство  . Перепишем степенной ряд в виде
. Перепишем степенной ряд в виде 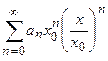 и рассмотрим ряд составленный из модулей членов этого ряда:
и рассмотрим ряд составленный из модулей членов этого ряда:
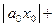

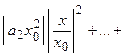
 .
.
В силу ограниченности каждого члена числового ряда 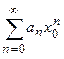 имеем неравенство:
имеем неравенство: 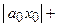

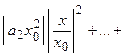
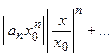

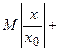
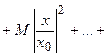
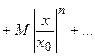
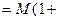

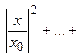
 .
.
Ряд, стоящий в круглых скобках, является суммой бесконечной геометрической прогрессии со знаменателем 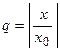 , которая имеет конечную сумму при
, которая имеет конечную сумму при 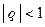 , следовательно, при
, следовательно, при  исходный степенной ряд мажорируется сходящимся рядом. По признаку сравнения данный ряд сходится. Пусть теперь существует такое число
исходный степенной ряд мажорируется сходящимся рядом. По признаку сравнения данный ряд сходится. Пусть теперь существует такое число  , для которого
, для которого 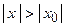 и при котором исходный ряд сходится. Так как бесконечная геометрическая прогрессия имеет бесконечную сумму при
и при котором исходный ряд сходится. Так как бесконечная геометрическая прогрессия имеет бесконечную сумму при 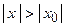 (
( ), то степенной ряд расходится при
), то степенной ряд расходится при 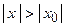 .
.
З1. Теорема Абеля утверждает, что если степенной ряд сходится в точке  (
( ), то он абсолютно сходится во всех точках интервала
), то он абсолютно сходится во всех точках интервала  (Рис. 22).
(Рис. 22).

 Рис. 22. Область сходимости степенного ряда.
Рис. 22. Область сходимости степенного ряда.

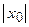
Если степенной ряд расходится в точке 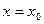 (
( ), то он абсолютно сходится во всех точках интервала
), то он абсолютно сходится во всех точках интервала 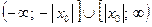 (Рис. 23).
(Рис. 23).
 Рис. 23. Область расходимости сте-
Рис. 23. Область расходимости сте-
 пенного ряда.
пенного ряда.

Отсюда вытекает теорема об интервале сходимости степенного ряда.
Т2. Если степенной ряд  сходится не при всех значениях величины
сходится не при всех значениях величины  и не только при
и не только при 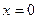 , то существует число
, то существует число 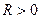 такое, что степенной ряд абсолютно сходится при
такое, что степенной ряд абсолютно сходится при 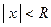 и расходится при
и расходится при  .
.
О2. Число 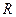 называется радиусом сходимости степенного ряда, а интервал
называется радиусом сходимости степенного ряда, а интервал 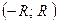 – интервалом сходимости.
– интервалом сходимости.
Рассмотрим теорему, которая дает алгоритм поиска радиуса сходимости 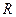 .
.
Док-во. Рассмотрим ряд  , составленный из модулей членов степенного ряда. По условию теоремы
, составленный из модулей членов степенного ряда. По условию теоремы  . Обозначим значение этого предела через
. Обозначим значение этого предела через  . Тогда
. Тогда 
 . При каждом значении
. При каждом значении 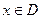 степенной ряд становится числовым. По признаку Даламбера ряд с фиксированным значением величины
степенной ряд становится числовым. По признаку Даламбера ряд с фиксированным значением величины  будет сходиться при выполнении неравенства
будет сходиться при выполнении неравенства  , т.е. при
, т.е. при 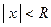 . Следовательно, степенной ряд сходится абсолютно при
. Следовательно, степенной ряд сходится абсолютно при 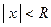 и расходится при
и расходится при  для всех
для всех 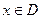 по признаку Даламбера.
по признаку Даламбера.
|
|
|
З2. Если  , то радиус сходимости
, то радиус сходимости 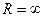 , т.е. степенной ряд сходится на всей числовой оси. Если
, т.е. степенной ряд сходится на всей числовой оси. Если 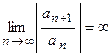 , то радиус сходимости
, то радиус сходимости 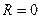 , т.е. степенной ряд сходится в единственной точке
, т.е. степенной ряд сходится в единственной точке 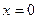 .
.
Пример 1. Найти радиусы и интервалы сходимости рядов а) 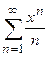 ; б)
; б) 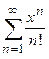 ; в)
; в)  .
.
а) Коэффициент 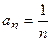 , следовательно,
, следовательно, 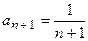 . Отсюда
. Отсюда
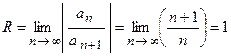 ,
,
таким образом, интервал сходимости равен  .
.
б) Коэффициент 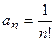 , следовательно,
, следовательно,  . Отсюда
. Отсюда
 ,
,
таким образом, степенной ряд сходится на всей числовой оси.
в) Коэффициент 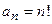 , следовательно,
, следовательно, 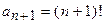 . Отсюда
. Отсюда
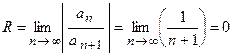 ,
,
таким образом, степенной ряд сходится только в точке 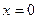 .
.
2. Разложение функций в степенные ряды.
Если функция 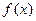 является суммой степенного ряда
является суммой степенного ряда
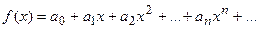 ,
,
который сходится на интервале  , то говорят, что на этом интервале функция
, то говорят, что на этом интервале функция 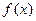 разлагается в степенной ряд по степеням аргумента
разлагается в степенной ряд по степеням аргумента  . Так как степенной ряд является частным случаем функционального ряда, то в случае равномерной сходимости этого ряда его можно почленно интегрировать и дифференцировать.
. Так как степенной ряд является частным случаем функционального ряда, то в случае равномерной сходимости этого ряда его можно почленно интегрировать и дифференцировать.
Т4. Если функция 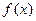 на интервале
на интервале  разлагается в степенной ряд, то это разложение единственно.
разлагается в степенной ряд, то это разложение единственно.
Док-во. Так как степенной ряд равномерно сходится на интервале  и функция
и функция 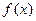 является его суммой, то его можно почленно дифференцировать:
является его суммой, то его можно почленно дифференцировать:
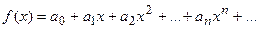 ;
;
 ;
;
 ;
;
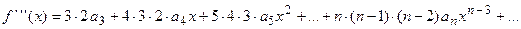 ;
;
………………………………………………………………………;
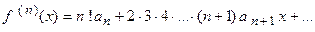 .
.
Полагая 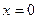 , найдем
, найдем
 ,
, 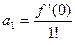 ,
,  ,
,  , …,
, …,  .
.
В силу того, что коэффициенты ряда 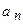 однозначно определяются значением функции
однозначно определяются значением функции 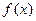 и ее производными в точке
и ее производными в точке 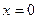 , то разложение функции
, то разложение функции 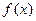 в степенной ряд единственно и имеет вид:
в степенной ряд единственно и имеет вид:


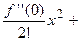

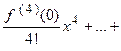
 .
.
Иначе говорят, что функция представлена в виде ряда Маклорена (см. Лекцию № 21, Первый семестр).
Пример 2. Разложить в ряд Маклорена функцию 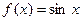 .
.
Найдем значения функции и ее производных вплоть до порядка  в точке
в точке 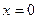
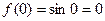 ;
;
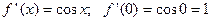 ;
;
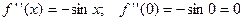 ;
;
 ;
;
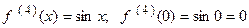 ;
;
 ;
;
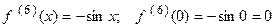 ;
;
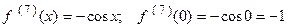 ;
;
………………………………………
Таким образом, разложение функции 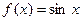 в ряд Маклорена имеет вид:
в ряд Маклорена имеет вид:
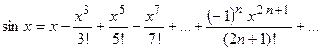 .
.
Приведем ряды Маклорена для некоторых наиболее часто используемых на практике элементарных функций: 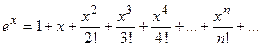 ;
;
|
|
|
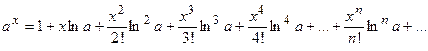 ;
;
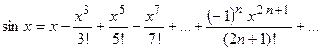 ;
;
 ;
;
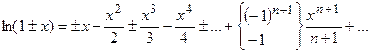 ;
;
 ;
;
 .
.
Если функция раскладывается в точке  , то она представляется степенным рядом Тейлора (см. Лекцию № 21, Первый семестр):
, то она представляется степенным рядом Тейлора (см. Лекцию № 21, Первый семестр):
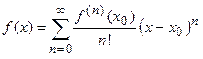 .
.
Пример 3. Используя стандартное разложение, представить в виде ряда Мак-лорена функцию 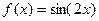 .
.
Воспользовавшись разложением в степенной ряд Маклорена функции  , получим:
, получим:  .
.
3. Применение степенных рядов.
1). Вычисление логарифмов. В основе вычислений логарифмов лежит ряд
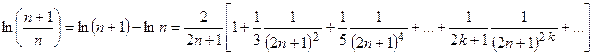 .
.
Пример 4. Вычислить 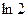 с точностью
с точностью  .
.
Полагая  , получим
, получим

 .
.
2). Вычисление корней. Для вычисления корней с большой точностью используют обобщенный бином Ньютона
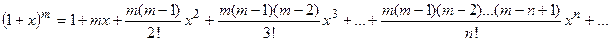 .
.
Например, требуется вычислить корень  -ой степени из числа
-ой степени из числа 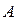 , прибли-
, прибли-
женное значение целой части которого равна  . Требуется уточнить это значение, для чего поступают следующим образом: полагают
. Требуется уточнить это значение, для чего поступают следующим образом: полагают 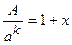 , тогда
, тогда
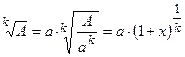 , следовательно,
, следовательно, 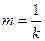 .
.
Пример 5. Вычислить 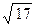 с точностью
с точностью  .
.
В данном примере 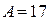 ,
,  ,
, 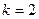 ,
, 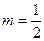 . Таким образом,
. Таким образом, 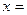

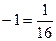 , следовательно,
, следовательно,  .
.
3). Вычисление неберущихся интегралов.
Пример 6. Вычислить интеграл  .
.
Данный интеграл является неберущимся, так как его первообразная не может быть выражена через элементарные функции (см. Лекцию № 6). Если положить  , то получим, что функцию
, то получим, что функцию 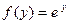 , которую можно представить в виде степенного ряда (см. выше)
, которую можно представить в виде степенного ряда (см. выше) 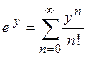 . Если вернуться к старой переменной, то получим
. Если вернуться к старой переменной, то получим  . Этот ряд равномерно сходится, поэтому его можно почленно интегрировать, т.е.
. Этот ряд равномерно сходится, поэтому его можно почленно интегрировать, т.е.
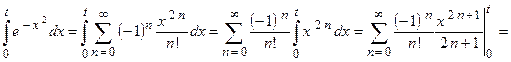
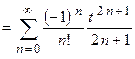 .
.
Пример 7. Вычислить интеграл 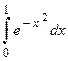 с точностью
с точностью  .
.
Используя результаты предыдущего примера, получим
 .
.
4). Решение дифференциальных уравнений.
Решение дифференциальных уравнений осуществляется с использованием
степенных рядов Тейлора  и Маклорена
и Маклорена 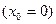 . Применение степенных рядов покажем на конкретном примере:
. Применение степенных рядов покажем на конкретном примере:
Пример 8. Найти четыре первых ненулевых члена ряда, являющегося решением задачи Коши: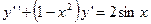 при начальных условиях
при начальных условиях 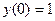 ;
;
 .
.
Так как в начальных условиях указано, что  , то представим искомую функцию в виде ряда Маклорена:
, то представим искомую функцию в виде ряда Маклорена:
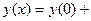
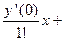
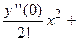

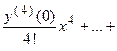
 .
.
Согласно начальным условиям  . Вторую производную функции выразим из самого дифференциального уравнения
. Вторую производную функции выразим из самого дифференциального уравнения 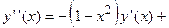
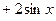 . Подставим в это выражение
. Подставим в это выражение  и учтем начальные условия, тогда вторая производная функции в точке
и учтем начальные условия, тогда вторая производная функции в точке  равна
равна 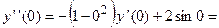
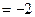 . Продифференцировав выражение для второй производной получим выражение для третьей производной функции
. Продифференцировав выражение для второй производной получим выражение для третьей производной функции 
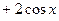 . Подставим в это выражение
. Подставим в это выражение 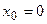 , получим
, получим
|
|
|
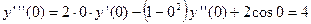 .
.
Так как это четвертый ненулевой член ряда Маклорена, то решение дифференциального уравнения с учетом начальных условий имеет вид:
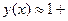


 .
.
Лекция № 23 “Тригонометрические ряды. Ряды Фурье”
1. Гармонический анализ. Тригонометрический ряд.
В науке и технике довольно часто приходится иметь дело с периодическими явлениями. Такие явления через определенный промежуток времени 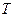 , называемый периодом, возвращают систему в начальное состояние. Из материала Лекции № 12 Первого семестра известно, что периодической функцией называется функция, удовлетворяющая равенству
, называемый периодом, возвращают систему в начальное состояние. Из материала Лекции № 12 Первого семестра известно, что периодической функцией называется функция, удовлетворяющая равенству 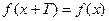 . Простейшей периодической функцией является синусоида
. Простейшей периодической функцией является синусоида  , где
, где 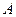 – амплитуда,
– амплитуда,  – частота,
– частота,  – начальная фаза. Очевидно, что сложение синусоид с разными амплитудами и одинаковыми частотами и фазами приводит к той же синусоиде с увеличенной амплитудой. Сложение же синусоид, различающихся амплитудами, частотами и фазами приводит к периодической функции, вид которой отличается от синусоиды.
– начальная фаза. Очевидно, что сложение синусоид с разными амплитудами и одинаковыми частотами и фазами приводит к той же синусоиде с увеличенной амплитудой. Сложение же синусоид, различающихся амплитудами, частотами и фазами приводит к периодической функции, вид которой отличается от синусоиды.
О1. Ряд вида


называется тригонометрическим рядом.
Из определения тригонометрического ряда видно, что периодическая функ
ция 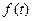 может быть представлена в виде суммы синусоид с различающими-ся амплитудами, частотами и фазами, т.е. может быть разложена на простые гармонические колебания.
может быть представлена в виде суммы синусоид с различающими-ся амплитудами, частотами и фазами, т.е. может быть разложена на простые гармонические колебания.
О2. Отдельные составляющие функции 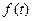 называются гармоническими составляющими или гармониками, а процесс разложения периодической функции на гармоники называется гармоническим анализом.
называются гармоническими составляющими или гармониками, а процесс разложения периодической функции на гармоники называется гармоническим анализом.
Если в качестве независимой переменной выбрать величину 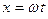 , то функция
, то функция 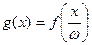 также будет периодической функцией, но уже со стандартным периодом
также будет периодической функцией, но уже со стандартным периодом  . Разложение этой функции в тригонометрический ряд имеет вид
. Разложение этой функции в тригонометрический ряд имеет вид
 .
.
Используя формулу  и вводя обозначения
и вводя обозначения  ,
, 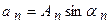 и
и  , приведем тригонометрический ряд к виду
, приведем тригонометрический ряд к виду  .
.
2. Ряд Фурье.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 774; Нарушение авторских прав?; Мы поможем в написании вашей работы!