Условия разложения функций в ряд Тейлора

Разложение функций в степенные ряды.

Теорема. Если в некотором интервале с центром в точке x₀ все производные 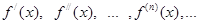ограничены одним и тем же числом (говорят тогда, что они ограничены по совокупности), то эта функция разлагается в ряд Тейлора.

Действительно, пусть производные обладают свойством ограниченности, т.е. пусть существует такое положительное число M>0, что для всех номеров n и для всех x из упомянутого выше интервала имеют место неравенства 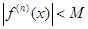. Запишем формулу Тейлора для f(x):

где x - некоторая точка, лежащая между точками x₀ и x. Так как f⁽ⁿ⁾(x) ограничена (для всех n), то .

Отношение 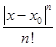стремится к нулю при любом заданном (зафиксированном) x и . В этом можно убедиться, формально рассмотрев ряд . По признаку Даламбера, он сходится, если

Но у нас: Поэтому и выполняется условие 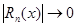при , в той окрестности точки x₀, в которой выполняются неравенства 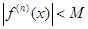, n= 1; 2;3;….

Итак, разность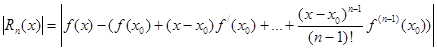

стремится к нулю с возрастанием n (т.е. стремится к нулю при ). С другой стороны, сумма есть не что иное, как частичная сумма ряда Тейлора: 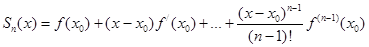. Получаем возможность записать такое равенство:

Оно означает, что сумма ряда Тейлора равна f(x).

Если разложение ведется в точке x₀ = 0, то имеем ряд Маклорена:

.

Дадим примеры разложения функций в ряд Маклорена:

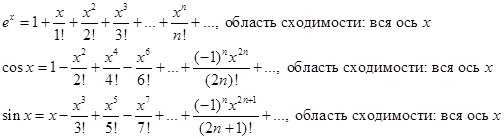
Еще одно важное разложение в ряд Маклорена:

Это так называемый биномиальный ряд. Радиус сходимости этого ряда равен 1, он сходится на интервале (-1,1). В частности, при m - целом, биномиальный ряд превращается в конечную сумму.

В частности:

Тогда:

Построим другие разложения: . Этот ряд сходится на всей числовой оси.

Еще пример:

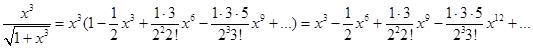
Некоторые приложения.

1) Вычисление значений функций. Например,

Еще: исходим из разложения

Взяв x= 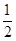, получим:

Извлечение корней. Найдем, например, 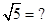Исходим из разложения

Тогда

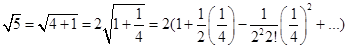
2) Вычисления интегралов

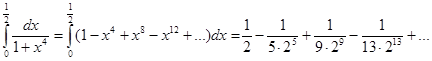
С другими примерами приложения рядов встретимся позже, например когда будем решать обыкновенные дифференциальные уравнения.

Дата добавления: 2014-01-11