
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Сравнение различных схем машинного представления графов. Преимущества, недостатки
|
|
|
|
Схемы машинного представления графов.
Основная терминология
Питання
1. Визначення точок локального екстремума функції. Навести приклади.
2. Визначення точок строгого локального екстремума функції. Навести приклади.
3. Якою буде похідна функції в точці локального мінімума (максімума)?
4. Геометричний зміст теореми Ферма.
5. Нехай. Чи може мати вісім нулів? Чи може мати сім нулів? Відповідь обгрунтувати.
6. Сформулювати і довести теорему Ролля.
7. Формула Лагранжа. Пояснити, чому теорема Ролля є частковим випадком теореми Лагранжа.
8. Сформулювати і довести теорему Лагранжа.
9. Геометричний зміст теореми Лагранжа.
10. Сформулювати і довести теорему Коші.
11. Пояснити, чому теорема Лагранжа є частковим випадком теореми Коші.
12. Чи може функція бути функцією похідної для деякої функції? Відповідь обгрунтувати.
13. Визначення похідної -го порядку.
- Основная терминология
Для наших целей граф 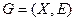 — это конечное множество вершин
— это конечное множество вершин 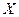 , или узлов, и конечное множество ребер
, или узлов, и конечное множество ребер 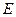 , которые суть неупорядоченные пары вершин. Граф называется помеченным, если каждая его вершина имеет некоторую метку – «имя». Чаще всего этой меткой является натуральное число.
, которые суть неупорядоченные пары вершин. Граф называется помеченным, если каждая его вершина имеет некоторую метку – «имя». Чаще всего этой меткой является натуральное число.
Введение графов имеет своей целью облегчить изучение разреженных матриц. Установим связь между матрицами и соответствующими им графами. Пусть 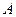 - симметричная
- симметричная 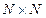 -матрица. Помеченный граф матрицы
-матрица. Помеченный граф матрицы 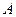 - это граф
- это граф 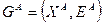 , для которого
, для которого 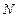 вершин
вершин 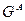 пронумерованы числами от 1 до
пронумерованы числами от 1 до 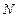 и пара вершин графа
и пара вершин графа 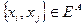 , т.е. является ребром графа, тогда и только тогда, когда
, т.е. является ребром графа, тогда и только тогда, когда  . Здесь
. Здесь 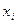 - узел
- узел 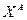 с меткой
с меткой 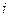 . Рис.1 иллюстрирует структуру матрицы (рис.1(а)) и ее помеченного графа (рис.1(б)).
. Рис.1 иллюстрирует структуру матрицы (рис.1(а)) и ее помеченного графа (рис.1(б)).

а б
Рис.1.
Если 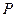 - произвольная
- произвольная 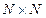 -матрица перестановки (см.лекц.8), то непомеченные графы матриц
-матрица перестановки (см.лекц.8), то непомеченные графы матриц 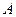 и
и 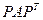 совпадают, а соответствующие помечивания различны. Таким образом, непомеченный граф
совпадают, а соответствующие помечивания различны. Таким образом, непомеченный граф 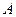 представляет структуру
представляет структуру 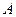 без упоминания о каком-либо конкретном упорядочении. Он изображает класс эквивалентности матриц
без упоминания о каком-либо конкретном упорядочении. Он изображает класс эквивалентности матриц 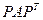 . Отыскание «хорошей» перестановки для
. Отыскание «хорошей» перестановки для 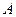 можно рассматривать как отыскание «хорошего» помечивания для ее графа. На рис.2 проиллюстрировано сказанное.
можно рассматривать как отыскание «хорошего» помечивания для ее графа. На рис.2 проиллюстрировано сказанное.
|
|
|
Два узла 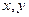 из графа
из графа 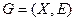 называются смежными, если
называются смежными, если 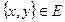 . Если
. Если 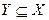 , то смежное множество для
, то смежное множество для 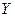 есть
есть
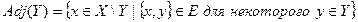 .
.
Иначе: 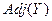 есть множество узлов
есть множество узлов 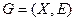 , не принадлежащих
, не принадлежащих 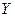 , но смежных хотя бы с одним узлом из
, но смежных хотя бы с одним узлом из 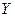 .
.
Для 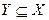 степень
степень 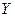 , обозначаемая через
, обозначаемая через 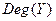 , есть число
, есть число 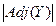 , где
, где 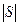 - обозначение числа элементов множества
- обозначение числа элементов множества 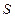 .
.
Если 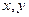 - различные узлы графа
- различные узлы графа 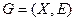 , то путем из
, то путем из 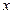 в
в  длины
длины 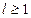 называется упорядоченное множество из
называется упорядоченное множество из 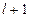 различных узлов
различных узлов 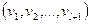 , такое, что
, такое, что 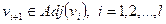 , причем
, причем  . Граф называется связным, если каждая пара различных узлов соединена хотя бы одним путем. В противном случае
. Граф называется связным, если каждая пара различных узлов соединена хотя бы одним путем. В противном случае 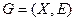 несвязен и состоит из двух или более связных компонент.
несвязен и состоит из двух или более связных компонент.
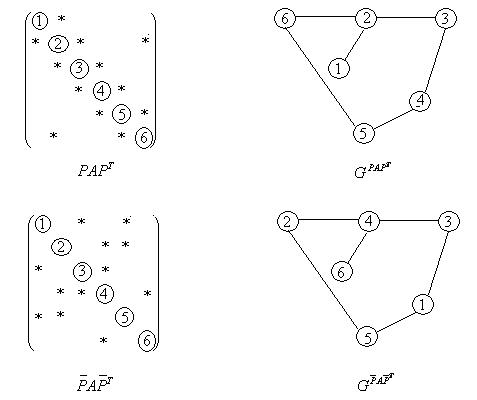
Рис.2.
- Схемы машинного представления графов
Характеристики алгоритмов, которые оперируют с графами, по обыкновению очень чувствительны к способу их представления.
Пусть 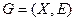 — неориентированный граф с
— неориентированный граф с 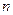 вершинами. Списком смежности для вершины
вершинами. Списком смежности для вершины 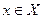 называется множество
называется множество
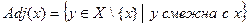
Структура смежности графа 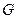 — это множество списков смежности для всех его вершин. Такую структуру можно реализовать, сохраняя последовательно списки смежности узлов в одномерном массиве
— это множество списков смежности для всех его вершин. Такую структуру можно реализовать, сохраняя последовательно списки смежности узлов в одномерном массиве 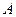 длины
длины 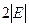 , и используя дополнительный индексный массив
, и используя дополнительный индексный массив 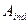 длины
длины 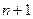 , который содержит указатели начала каждого списка смежности в массиве
, который содержит указатели начала каждого списка смежности в массиве 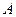 (
(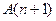 — адрес первой свободной ячейки в массиве
— адрес первой свободной ячейки в массиве 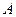 ) (рис.3). Общая длина массивов при такой схеме хранения —
) (рис.3). Общая длина массивов при такой схеме хранения — 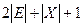 .
.
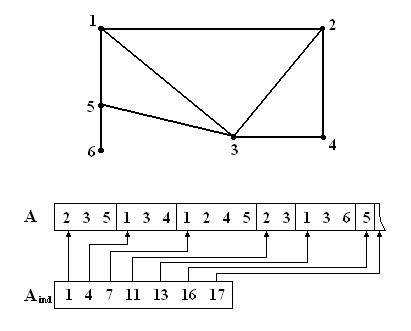
Рис.3. Пример структуры смежности графа
Соседи текущего узла 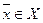 в массиве
в массиве 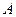 располагаются в позициях, начиная с
располагаются в позициях, начиная с 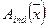 и заканчивая
и заканчивая 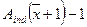 , таким образом, их поиск не является сложным, что есть очень значительным преимуществом рассмотренной схемы хранения. Однако внесение при необходимости изменений в структуру смежности графа очевидно вызовет затруднение. Действительно, добавление (исключение) узлов (ребер) из графа приведет к модификации не только списков смежности соответствующих узлов, но может потребовать изменения всего массива
, таким образом, их поиск не является сложным, что есть очень значительным преимуществом рассмотренной схемы хранения. Однако внесение при необходимости изменений в структуру смежности графа очевидно вызовет затруднение. Действительно, добавление (исключение) узлов (ребер) из графа приведет к модификации не только списков смежности соответствующих узлов, но может потребовать изменения всего массива 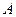 (и соответствующим образом
(и соответствующим образом 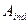 ) (рис.4), что, конечно, не желательно.
) (рис.4), что, конечно, не желательно.
|
|
|
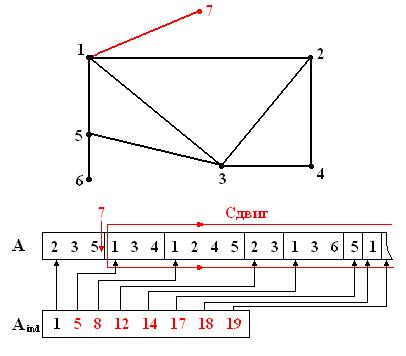
Рис.4. Модификация структуры смежности графа при добавлении вершины
 Данная проблема очевидно остается нерешенной и при использовании для представления графа
Данная проблема очевидно остается нерешенной и при использовании для представления графа 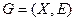 нижней структуры смежности. Здесь вместо хранения для каждого узла
нижней структуры смежности. Здесь вместо хранения для каждого узла 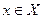 полного списка смежности сохраняются только те узлы из
полного списка смежности сохраняются только те узлы из 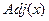 , метки которых больше, чем у
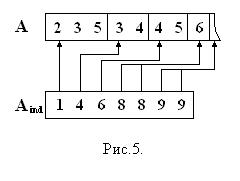
, метки которых больше, чем у 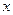 , что может значительно сократить запросы к памяти. Для графа, представленного на рис.3, нижняя структура смежности изображена на рис.5. Общая длина массивов при такой схеме хранения —
, что может значительно сократить запросы к памяти. Для графа, представленного на рис.3, нижняя структура смежности изображена на рис.5. Общая длина массивов при такой схеме хранения — 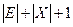 : длина массива
: длина массива 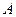 уменьшилась в два раза по сравнению с хранением всей структуры смежности, поскольку теперь каждое ребро будет учтено лишь 1 раз (для той из двух инцидентных ему вершин, номер которой меньше).
уменьшилась в два раза по сравнению с хранением всей структуры смежности, поскольку теперь каждое ребро будет учтено лишь 1 раз (для той из двух инцидентных ему вершин, номер которой меньше).
Одной из наиболее простых схем хранения графа является таблица связей - двумерный массив, который имеет 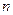 строк и
строк и 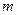 столбцов, где
столбцов, где 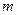 — максимальная степень вершин в
— максимальная степень вершин в 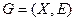 . Список смежности
. Список смежности 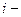 го узла сохраняется в
го узла сохраняется в 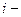 ой строке. Для графа, приведенного на рис.3, таблица связей будет иметь вид:
ой строке. Для графа, приведенного на рис.3, таблица связей будет иметь вид:
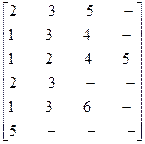 .
.
Данная схема хранения чрезвычайно проста при реализации, доступ к списку смежности очередного узла - доступ к соответствующей строке матрицы, модификация графа приводит к изменению элементов соответствующих строк матрицы без нарушения общей структуры (если при модификации не изменяется 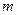 ). Однако эта схема может быть чрезвычайно неэффективной, если большое количество узлов графа имеет степень, (значительно) меньшую, чем максимальная, поскольку ее требования к памяти определяются как
). Однако эта схема может быть чрезвычайно неэффективной, если большое количество узлов графа имеет степень, (значительно) меньшую, чем максимальная, поскольку ее требования к памяти определяются как 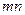 «сохраняемых» элементов.
«сохраняемых» элементов.
Наиболее удобной с точки зрения возможностей проведения модификаций графа является схема, которая использует поле связей. Данная схема содержит три одномерных массива 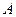 ,
, 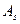 ,
, 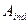 , первые два из которых имеют длины
, первые два из которых имеют длины 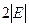 , последний —
, последний — 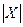 . Значением указателя
. Значением указателя 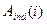 является начало списка смежности
является начало списка смежности 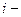 го узла в массиве
го узла в массиве 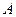 . Если
. Если 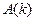 — это очередной сосед
— это очередной сосед 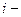 го узла, то
го узла, то 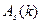 — указатель места расположения следующего его соседа в массиве
— указатель места расположения следующего его соседа в массиве 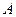 . Отрицательное значение
. Отрицательное значение 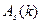 говорит об окончании списка смежности рассматриваемого узла.
говорит об окончании списка смежности рассматриваемого узла.
|
|
|
Общая длина массивов при таком способе представления графа — 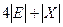 , что значительно больше, чем в первой схеме. Однако модификация графа требует лишь незначительных изменений в уже сформированной части массивов. Для графов, представленных на рис.3,4, соответствующие схемы - на рис.6.
, что значительно больше, чем в первой схеме. Однако модификация графа требует лишь незначительных изменений в уже сформированной части массивов. Для графов, представленных на рис.3,4, соответствующие схемы - на рис.6.

Рис.6. Схема хранения, основанная на поле связей: исходный граф (а); граф после добавления вершины (б)
- Сравнение различных схем машинного представления графов. Преимущества, недостатки
Схема хранения графа 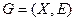
| Преимущества | Недостатки | Общие запросы к памяти |
| Основанная на структуре смежности графа | Простая организация поиска соседей текущего узла | Вызывает трудности внесение изменений в структуру смежности графа. Добавление (исключение) узлов (ребер) из графа приведет к модификации всего массива 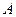 и и 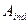
| 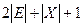
|
| Основанная на нижней структуры смежности графа | Простая организация поиска соседей текущего узла Значительное сокращение запросов к памяти по сравнению со схемой, основанной на структуре смежности графа | Вызывает трудности внесение изменений в структуру смежности графа. Добавление (исключение) узлов (ребер) из графа приведет к модификации всего массива 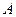 и и 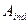
| 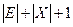
|
| Таблица связей | Схема проста при реализации, доступ к списку смежности узла - доступ к соответствующей строке матрицы; модификация графа приводит к изменению элементов соответствующих строк матрицы без нарушения общей структуры (если при модификации не изменяется 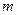 ). ).
| Схема может быть чрезвычайно неэффективной, если большое количество узлов графа имеет степень, значительно меньшую, чем максимальная | 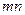
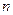 - количество вершин, - количество вершин, 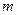 — максимальная степень вершин в — максимальная степень вершин в 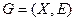
|
| Основанная на поле связей | Наиболее удобна для модификаций графа | Наибольшие запросы к памяти по сравнению со всеми рассмотренными схемами | 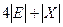
|
|
|
|
Таким образом, выбор схемы хранения графа определяется тем набором задач, которые решаются на его основе.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 483; Нарушение авторских прав?; Мы поможем в написании вашей работы!