Функції Ляпунова

Нагадаємо, що система диференційних рівнянь 1-го порядку 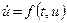називається автономною, якщо вектор-функція f не має явної залежності від мінної t тобто 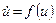(8)

Тут u – це n -вимірний вектор, – відома гладка вектор-функція.

Нехай f (0) = 0, тоді нульова функція u (t) º 0 буде розв’язком цієї системи і можна поставити питання про стійкість цього розв’язку.

Як правило, у такого типу задачах не вдається знайти загальний розв’язок системи (8) у явному аналітичному виді (ні в елементарних функціях, ні у квадратурах) і досліджувати нульовий розв’язок на стійкість, виходячи з визначення . Тому задачі стійкості є задачами т.зв. якісної теорії диференційних рівнянь, а для одержання відповіді на питання доводиться використати всякого роду непрямі ознаки. Один з підходів – це побудова функції Ляпунова для системи (8) і застосування однієї з теорем Ляпунова.

Щоб сформулювати ці теореми необхідне поняття системної похідної. Звичайно, якщо деяка скалярна функція v має в якості аргументу вектор 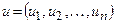, а сам вектор u залежить від скалярної змінної t, то похідна має вигляд: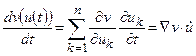

Системна похідна функції 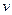відрізняється від цієї загальної формули тим, що коли u (t) є розв’язком системи (8), то 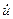можна замінити на f (u) тобто 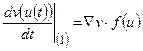(9)

Перейдемо тепер безпосередньо до формулювань самих теорем. Всі вони починаються однаково: Нехай в околі нуля 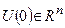задана неперервна диференційована функція v (u) причому v(0) = 0. Далі йдуть розходження:

1) Якщо v (u) > 0 для всіх ненульових 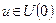і для всіх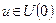 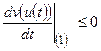, то нульовий розв’язок системи (8) стійкий за Ляпуновим.

2) Якщо v (u) > 0 і для всіх ненульових 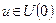, то нульовий розв’язок системи (3.4.8.) асимптотично стійкий за Ляпуновим.

3) Якщо існують як завгодно близькі до нуля точки 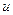, у яких v (u) > 0 і якщо для всіх ненульових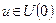 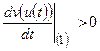, то нульовий розв’язок системи (8 ) нестійк ий.

Значну важливість для практики представляють системи другого порядку, тобто коли тоді система 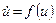у координатній формі запису має вигляд

де 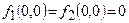, та в цьому випадку для функції Ляпунова 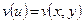системна похідна має такий вигляд:

Загального методу побудови функції Ляпунова немає. Як перші спроби вибору функції можна спробувати

й т.д.

Параметри вибираються належним чином, щоб задовольнити умовам якої-небудь із теорем.

Дата добавления: 2014-01-11