
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные теоремы о пределах. Теорема 14.1. Если существуют и , то существует и
|
|
|
|
Теорема 14.1. Если существуют  и
и  , то существует и
, то существует и 
Доказательство. Используя третье определение предела, представим f(x)=A+α(x), g(x)=B+β(x), где α(х) и β(х) – бесконечно малые при х→х0. Тогда f(x)+g(x)=A+B+(α(x)+β(x))=A+B+γ(x), где γ(х)=α(х)+β(х) – бесконечно малая. Следовательно, 
Теорема 14.2. Если существуют  и
и  , то существует и
, то существует и 
Доказательство. Представим f(x)=A+α(x), g(x)=B+β(x), где α(х) и β(х) – бесконечно малые при х→х0. Тогда f(x)·g(x)=AB+Aβ(x)+Bα(x)+α(x)β(x). Но Aβ(x)+Bα(x)+α(x)β(x) – бесконечно малая (так как f(x) и g(x) ограничены в окрестности х0), следовательно, 
Теорема 14.3. Если существуют  и
и  , то существует и
, то существует и

Доказательство. Представим f(x)=A+α(x), g(x)=B+β(x), где α(х) и β(х) – бесконечно малые при х→х0. Тогда 
где  ограниченная в окрестности х0 функция, так как имеет предел, равный 1/В², а Вα(х)-Аβ(х) – бесконечно малая. Поэтому
ограниченная в окрестности х0 функция, так как имеет предел, равный 1/В², а Вα(х)-Аβ(х) – бесконечно малая. Поэтому  - бесконечно малая, и
- бесконечно малая, и 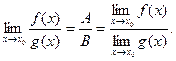
Теорема 14.4 («лемма о двух милиционерах»). Если f(x) ≤ φ(x) ≤ g(x) в некоторой окрестности х0 и 
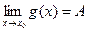 , то существует и
, то существует и  .
.
Доказательство. Из условия теоремы следует, что f(x)-A≤φ(x)-A≤g(x)-A. Выберем δ-окрестность точки х0, в которой |f(x)-A|<ε и |g(x)-A|<ε. Тогда –ε< f(x)-A≤φ(x)-A≤g(x)-A<ε. Поэтому |φ(x)-A|<ε, следовательно,  .
.
Теорема 14.5. Если при х→х0 f(x)≥0 и  , то А≥0.
, то А≥0.
Доказательство. Предположим, что А<0. Тогда, выбрав ε=|A|/2, найдем окрестность точки х0, в которой |f(x)-A|<|A|/2, следовательно, 3А/2<f(x)<A/2, то есть f(x)<0 в рассматриваемой окрестности, что противоречит условию теоремы.
Следствие 1. Аналогично доказывается, что если f(x)≤0, то А≤0.
Следствие 2. Если f(x)≥g(x) и обе функции имеют пределы в точке х0, то 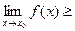

Замечание. Все перечисленные утверждения можно доказать для 
|
|
|
Теорема 14.6 (без доказательства). Ограниченная и возрастающая при a<x<b (a<x< ) функция имеет предел при х
) функция имеет предел при х (х
(х ).
).
Замечательные пределы.
Теорема 14.7 (первый замечательный предел).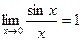 .
.
Доказательство. Рассмотрим окружность единичного радиуса с центром в начале координат и будем считать, что угол АОВ равен х (радиан). Сравним площади треугольника АОВ, сектора АОВ и треугольника АОС, где прямая ОС – касательная к окружности, проходящая через точку (1;0). Очевидно, что  .
.




у
B C







A x
Используя соответствующие геометрические формулы для площадей фигур, получим отсюдa, что 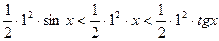 , или sinx<x<tgx. Разделив все части неравенства на sinx (при 0<x<π/2 sinx>0), запишем неравенство в виде:
, или sinx<x<tgx. Разделив все части неравенства на sinx (при 0<x<π/2 sinx>0), запишем неравенство в виде: 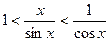 .
.
Тогда 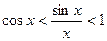 , и по теореме 14.4
, и по теореме 14.4 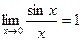 .
.
Замечание. Доказанное справедливо и при x<0.
Cледствия из первого замечательного предела.
1. 
2. 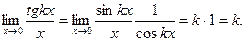
3. 
4. 
5.  где y = arcsinx.
где y = arcsinx.
6.  где y = arctgx.
где y = arctgx.
7. 
Теорема 14.8 (второй замечательный предел).  .
.
Замечание. Число е 2,7.
2,7.
Доказательство.
1. Докажем сначала, что последовательность  при
при  имеет предел, заключенный между 2 и 3. По формуле бинома Ньютона
имеет предел, заключенный между 2 и 3. По формуле бинома Ньютона
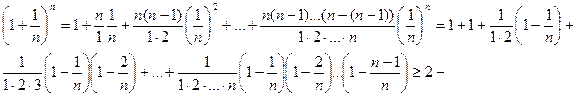
возрастающая переменная величина при возрастающем n. С другой стороны,
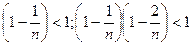 и т.д., поэтому
и т.д., поэтому
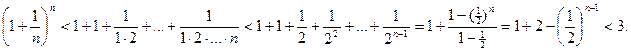
Следовательно, 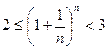 - ограниченная и возрастающая величина, поэтому она имеет предел (см. теорему 14.6). Значение этого предела обозначается числом е.
- ограниченная и возрастающая величина, поэтому она имеет предел (см. теорему 14.6). Значение этого предела обозначается числом е.
2. Докажем, что  .
.
а) Пусть  . Тогда
. Тогда 
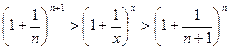 . При
. При 
 . Найдем пределы левой и правой частей неравенства:
. Найдем пределы левой и правой частей неравенства:


Следовательно, по теореме 14.4  .
.
б) Если  то
то 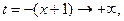 и
и  Теорема доказана.
Теорема доказана.
Следствия из второго замечательного предела.
1. 
2. 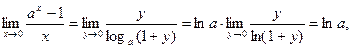 где a > 0, y = ax - 1.
где a > 0, y = ax - 1.
3. 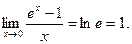
Натуральный логарифм и гиперболические функции.
Определение 14.2. Логарифм с основанием е называется натуральным логарифмом.
Обозначение: logex=ln x.
Определение 14.3. Функции  (гиперболический синус),
(гиперболический синус),  (гиперболический косинус),
(гиперболический косинус),  (гиперболический тангенс) и
(гиперболический тангенс) и  (гиперболический котангенс) называются гиперболическими функциями.
(гиперболический котангенс) называются гиперболическими функциями.
|
|
|
Замечание 1. Гиперболические функции обладают некоторыми свойствами, похожими на свойства обычных тригонометрических функций. Например,
сh²x – sh²x = ¼(e2x + 2 + e-2x - e2x + 2 - e-2x)=1,
2 shx chx = 2
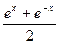 =
=  =sh2x,
=sh2x,
thx=shx/chx, cthx=chx/shx,
thx·cthx = 
 =1 и т.д.
=1 и т.д.
Замечание 2. Термин «гиперболические» объясняется тем, что уравнения
x = a ch t, y = a sh t, a>0, 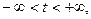
являются параметрическими уравнениями правой ветви гиперболы x² - y² = a², так же, как x = a cost, y = a sint (0≤t≤2π) – параметрические уравнения окружности x²+y²=a².
Лекция 15.
Сравнение бесконечно малых. Символы «о» и «О». Эквивалентные бесконечно малые, их применение к вычислению пределов. Бесконечно большие функции и их связь с бесконечно малыми.
Рассмотрим функции α(х) и β(х), для которых  то есть бесконечно малые в окрестности х0.
то есть бесконечно малые в окрестности х0.
1. Если  то α(х) и β(х)называются бесконечно малыми одного порядка. В частности, если А=1, говорят, что α(х) и β(х) – эквивалентные бесконечно малые.
то α(х) и β(х)называются бесконечно малыми одного порядка. В частности, если А=1, говорят, что α(х) и β(х) – эквивалентные бесконечно малые.
2. Если  то α(х) называется бесконечно малой более высокого порядка по сравнению с β(х).
то α(х) называется бесконечно малой более высокого порядка по сравнению с β(х).
3. Если  , то α(х) есть бесконечно малая порядка n по сравнению с β(х).
, то α(х) есть бесконечно малая порядка n по сравнению с β(х).
Обозначения: α(х)=О(β(х)) – бесконечно малые одного порядка, α(х)~β(х) – эквивалентные бесконечно малые, α(х)=о(β(х)) – α есть бесконечно малая более высокого порядка, чем β.
Замечание 1. Используя 1-й и 2-й замечательные пределы и их следствия, можно указать бесконечно малые функции при х→0, эквивалентные х: sinx, tgx, arcsinx, arctgx, ln(1+x), ex-1.
Замечание 2. При раскрытии неопределенности вида 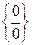 , то есть предела отношения двух бесконечно малых, можно каждую из них заменять на эквивалентную – эта операция не влияет на существование и величину предела.
, то есть предела отношения двух бесконечно малых, можно каждую из них заменять на эквивалентную – эта операция не влияет на существование и величину предела.
Пример.

Бесконечно большие функции.
Определение 15.1. Функция f(x) называется бесконечно большой при х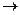 х0, если
х0, если

Для бесконечно больших можно ввести такую же систему классификации, как и для бесконечно малых, а именно:
1. Бесконечно большие f(x) и g(x) считаются величинами одного порядка, если
 .
.
2. Если 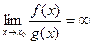 , то f(x) считается бесконечно большой более высокого порядка, чем g(x).
, то f(x) считается бесконечно большой более высокого порядка, чем g(x).
3. Бесконечно большая f(x) называется величиной k-го порядка относительно бесконечно большой g(x), если  .
.
|
|
|
Замечание. Отметим, что ах – бесконечно большая (при а>1 и х ) более высокого порядка, чем xk для любого k, а logax – бесконечно большая низшего порядка, чем любая степень хk.
) более высокого порядка, чем xk для любого k, а logax – бесконечно большая низшего порядка, чем любая степень хk.
Теорема 15.1. Если α(х) – бесконечно малая при х→х0, то 1/α(х) – бесконечно большая при х→х0.
Доказательство. Докажем, что 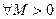
 при |x - x0| < δ. Для этого достаточно выбрать в качестве ε 1/M. Тогда при |x - x0| < δ |α(x)|<1/M, следовательно,
при |x - x0| < δ. Для этого достаточно выбрать в качестве ε 1/M. Тогда при |x - x0| < δ |α(x)|<1/M, следовательно,
|1/α(x)|>M. Значит,  , то есть 1/α(х) – бесконечно большая при х→х0.
, то есть 1/α(х) – бесконечно большая при х→х0.
Лекция 16.
Непрерывность функции в точке. Локальные свойства непрерывных функций. Непрерывность сложной и обратной функций. Непрерывность элементарных функций. Точки разрыва функций и их классификация. Свойства функций, непрерывных на отрезке: ограниченность, существование наибольшего и наименьшего значений, промежуточные значения.
Определение 16.1. Функция y=f(x) называется непрерывной в точке х0, если

Замечание. Из этого определения следует, во-первых, что функция определена при х = = х0, и во-вторых, что при х→х0 существует конечный предел функции.
Свойства непрерывных функций.
1. Если функции f(x) и g(x) непрерывны при х = х0, то f(x)+g(x) тоже непрерывна при х = х0.
2. Если функции f(x) и g(x) непрерывны при х = х0, то f(x)g(x) тоже непрерывна при х = х0.
3. Если функции f(x) и g(x) непрерывны при х = х0, то f(x)/g(x) тоже непрерывна при х = х0 при условии, что g(x0) ≠ 0.
4. Если u=φ(x) непрерывна при х = х0, а f(u) непрерывна при u = u(x0), то сложная функция f(φ(x)) непрерывна при х = х0.
Доказательства всех перечисленных свойств непосредственно следуют из соответствующих свойств пределов.
Точки разрыва и их классификация.
Определение 16.2. Пусть функция f(x) определена в некоторой окрестности точки х0, за исключением, возможно, самой этой точки. Тогда х0 называется точкой разрыва функции f(x), если она либо не определена при х = х0, либо не является непрерывной в точке х0.
Определение 16.3. Если существует конечный предел f(x) при х→х0, но не равный f(x0), точка разрыва х0 называется устранимой особенностью.
|
|
|
Замечание. Термин «устранимая особенность» связан с тем, что, доопределив функцию в точке разрыва значением ее предела в этой точке, мы сделаем ее непрерывной при х = х0, то есть устраним разрыв в рассматриваемой точке.
Определение 16.4. Если существуют конечные односторонние пределы f(x) при х→х0, точка х0 называется точкой разрыва 1-го рода.
Определение 16.5. Все остальные точки разрыва называются точками разрыва 2-го рода.
Примеры.
1. 
 Функция не определена при х = 1, а для остальных значений аргумента может быть представлена как у = х - 2. Следовательно,
Функция не определена при х = 1, а для остальных значений аргумента может быть представлена как у = х - 2. Следовательно,  , то есть х = 1 – устранимая особенность.
, то есть х = 1 – устранимая особенность.
2. 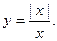 Из определения модуля следует, что у = 1 при x > 0, y = -1 при x < 0, а при х = 0 функция не определена. При этом
Из определения модуля следует, что у = 1 при x > 0, y = -1 при x < 0, а при х = 0 функция не определена. При этом  . Следовательно, х = 0 –точка разрыва 1-го рода.
. Следовательно, х = 0 –точка разрыва 1-го рода.
3. 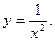 Функция не определена при х = 0, и
Функция не определена при х = 0, и  . Поэтому х = 0 – точка разрыва 2-го рода.
. Поэтому х = 0 – точка разрыва 2-го рода.
4. 
 то есть правосторонний предел не является конечным. Значит, х = 0 – точка разрыва 2-го рода.
то есть правосторонний предел не является конечным. Значит, х = 0 – точка разрыва 2-го рода.
5.  Функция не определена при х = 0 и не имеет предела при х→0. Следовательно, х = 0 – точка разрыва 2-го рода.
Функция не определена при х = 0 и не имеет предела при х→0. Следовательно, х = 0 – точка разрыва 2-го рода.
Свойства функций, непрерывных на отрезке.
Определение 16.6. Функция y=f(x) называется непрерывной на отрезке [ab], если она непрерывна в каждой точке этого отрезка (при этом f(a) и f(b) равны соответствующим односторонним пределам).
Теорема 16.1. Функция f(x), непрерывная на отрезке [ab], ограничена на нем.
Доказательство. По 1-му свойству предела существует окрестность точки х = а, в которой f(x) ограничена, то есть существуют числа m0 и М0: m0<f(x)<M0 в рассматриваемой окрестности. Выберем точку в правой части этой окрестности и рассмотрим окрестность этой точки, в которой f(x) тоже ограничена. Продолжим эту процедуру до тех пор, пока весь отрезок [ab] не будет покрыт системой из n окрестностей, причем для каждой i-й окрестности mi<f(x)<Mi. Следовательно, для любого х, принадлежащего отрезку [ab], верно неравенство: m<f(x)<M, где m=min(mi), M=max(Mi). Значит, f(x) ограничена на [ab].
Замечание. Для доказательства следующего свойства функции, непрерывной на отрезке, введем понятие точной верхней и нижней грани числового множества.
Определение 16.7. Если множество Х ограничено сверху, то наименьшее из чисел, ограничивающих его сверху, называется его верхней гранью. Нижней гранью называется наибольшее из чисел, ограничивающих множество снизу.
Обозначения: В=supX – верхняя грань, А=infX – нижняя грань.
Замечание 1. Можно дать другое определение верхней и нижней грани, эквивалентное предыдущему: число В называется верхней гранью числового множества Х, если:
1) x
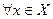
2) 


Аналогично число А называется нижней гранью числового множества Х, если:
1) 
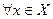
2) 

Замечание 2. Можно доказать, что всякое непустое ограниченное сверху (снизу) числовое множество имеет верхнюю (нижнюю) грань. Следовательно, верхняя и нижняя грань существует для значений функции, ограниченной на отрезке.
Теорема 16.2. Если функция у=f(x) определена и непрерывна на отрезке [ab], то она достигает на нем своей верхней и нижней грани.
Доказательство. Ограниченность f(x) на [ab] следует из теоремы 16.1. Пусть М=supf(x).
Предположим, что f(x)<M на [ab], и рассмотрим вспомогательную функцию
 . По выдвинутому предположению знаменатель дроби в 0 не обращается, следовательно, g(x) непрерывна на [ab] и поэтому ограничена (т.16.1):
. По выдвинутому предположению знаменатель дроби в 0 не обращается, следовательно, g(x) непрерывна на [ab] и поэтому ограничена (т.16.1):
g(x) Но из этого следует, что
Но из этого следует, что 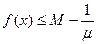 , то есть число
, то есть число  , меньшее М, оказывается верхней гранью f(x), что противоречит выбору М. Значит, на [ab] найдется значение х0 такое, что f(x0)=M. Аналогичным образом можно доказать и то, что f(x) достигает на [ab] своей нижней грани.
, меньшее М, оказывается верхней гранью f(x), что противоречит выбору М. Значит, на [ab] найдется значение х0 такое, что f(x0)=M. Аналогичным образом можно доказать и то, что f(x) достигает на [ab] своей нижней грани.
Теорема 16.3. Если функция y=f(x) непрерывна на отрезке [ab] и f(a)=A, f(b)=B, то для любого числа С, заключенного между А и В, найдется х0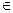 [ab]: f(x0)=C.
[ab]: f(x0)=C.
Доказательство. Пусть для определенности A<C<B. Найдем середину отрезка [ab]: х =(а+в)/2. Если при этом f(x)=C, то искомое значение х0 найдено. В противном случае выберем ту половину отрезка, на концах которой значения f(x) лежат по разные стороны С, и обозначим ее концы а1 и b1. Будем продолжать эту процедуру (деления отрезка пополам и выбора соответствующей половины). Тогда либо через конечное число шагов значение функции в середине очередного отрезка станет равно С, либо мы получим две последовательности ({an}- начальных точек выбранных отрезков и {bn}- их конечных точек), имеющие своими пределами одну и ту же общую для всех отрезков точку х0. Тогда в силу непрерывности f(x) 
Но, поскольку отрезки выбирались так, что f(an) < C < f(bn), получим, что
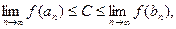 то есть f(x0) ≤ C ≤ f(x0), или С = f(x0).
то есть f(x0) ≤ C ≤ f(x0), или С = f(x0).
Следствие.
Если функция непрерывна на отрезке и принимает на его концах значения разных знаков, то на отрезке найдется хотя бы одна точка, в которой значение функции равно нулю.





Непрерывность обратной функции.
Лемма. Если функция f(x) строго возрастает на [ab] и f(a)=A, f(b)=B, то существует обратная функция f-1(x), строго возрастающая на [AB].
Доказательство. Докажем существование обратной функции, то есть ее однозначность. Действительно, если существует у=f(x1)=f(x2), то это противоречит условию монотонности f(x): если х1 < x2, то f(x1) < f(x2), а если x1 > x2, то f(x1) > f(x2).
Докажем возрастание f-1 на [AB]. Пусть y1 = f(x1) < y2 = f(x2). Тогда, если х1 = х2, то f(x1) = =f(x2); если х1 > x2, f(x1) > f(x2). Оба эти случая противоречат выбору у1 и у2. Значит, х1 < x2, то есть f-1(y1)<f-1(y2). Лемма доказана.
Теорема 16.4. Если функция f(x) строго возрастает и непрерывна на [ab] и f(a)=A, f(b)=B, то множеством значений f(x) является отрезок [AB], и обратная функция f-1(x) является непрерывной и строго возрастающей на [AB].
Доказательство. Неравенство A = f(a) < f(x) < f(b) = B для a < x < b следует из возрастания f(x). С другой стороны, любое значение из интервала (АВ) будет достигаться при некотором х из интервала (аb) по теореме 16.3. Возрастание обратной функции следует из леммы. Остается доказать непрерывность f-1. Если допустить, что на (АВ) существует точка разрыва, то из условия a ≤ f-1 ≤ b следует, что может наблюдаться только разрыв 1-го рода. Но, если односторонние пределы в точке такого разрыва не равны между собой, то обратная функция не может принимать значений, лежащих между односторонними пределами (так как функция монотонна, и левосторонний предел может быть только меньше правостороннего), а это противоречит доказанному утверждению, что обратная функция принимает все значения из интервала [AB]. Значит, f-1 непрерывна на [AB]. Теорема доказана.
Непрерывность элементарных функций.
1. Так как функции у=С и у=х непрерывны, то из свойств непрерывных функций следует непрерывность любого многочлена и непрерывность дробно-рациональной функции при всех значениях х, кроме тех, при которых знаменатель дроби обращается в 0.
2. Для доказательства непрерывности показательной функции воспользуемся тем, что
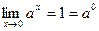 , то есть ах непрерывна при х=0. Но
, то есть ах непрерывна при х=0. Но  Следовательно,
Следовательно, 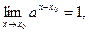 то есть
то есть  , и показательная функция непрерывна при всех значениях аргумента. Отсюда следует непрерывность гиперболических функций.
, и показательная функция непрерывна при всех значениях аргумента. Отсюда следует непрерывность гиперболических функций.
3. Непрерывность логарифмической функции на любом конечном отрезке следует из теоремы 16.4, так как логарифмическая функция является обратной к показательной.
4. Докажем непрерывность функции y=sinx. sinx < x для  , тогда |sinx| < |x| для любого х. Отсюда
, тогда |sinx| < |x| для любого х. Отсюда 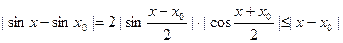 , что доказывает непрерывность функции при выборе ε = δ = |x - x0|.
, что доказывает непрерывность функции при выборе ε = δ = |x - x0|.
Из непрерывности функции y = sinx, в свою очередь, следует непрерывность остальных тригонометрических функций: 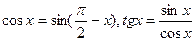 и т.д. и непрерывность обратных тригонометрических функций.
и т.д. и непрерывность обратных тригонометрических функций.
Следовательно, все элементарные функции непрерывны во всей области своего определения.
Лекция 17.
Производная функции, ее геометрический и механический смысл. Уравнение касательной к графику функции. Дифференцируемость функции, ее связь с непрерывностью. Дифференциал функции, его геометрический смысл. Линеаризация функции.
Рассмотрим функцию y=f(x), заданную в окрестности точки х0.
Определение 17.1. Если существует конечный предел  , то он называется производной функции f в точке х0.
, то он называется производной функции f в точке х0.
Обозначение: 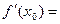
 .
.
Разность называется приращением аргумента, а
называется приращением аргумента, а  - приращением функции. Таким образом, можно определить производную как
- приращением функции. Таким образом, можно определить производную как  .
.
Геометрический смысл производной.
 | |||
 | |||
 у Рассмотрим график функции у=f(x) и проведем
у Рассмотрим график функции у=f(x) и проведем
В секущую через точки А с абсциссой х0 и В с


 абсциссой х0+Δх. Если обозначить разность
абсциссой х0+Δх. Если обозначить разность
ординат этих точек Δу, то тангенс угла α, образо-
А ванного секущей с осью Ох, можно представить
так:  . ЕслиΔх→0, точка В переме-
. ЕслиΔх→0, точка В переме-
щается по кривой, приближаясь к точке А, и
α0 α х0 х секущая при совпадении точек В и А превра-
щается в касательную к графику функции,
образующую с осью Ох угол α0. При этом 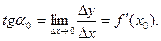 Следовательно, значение производной при данном значении х равно тангенсу угла, образованного касательной к графику функции в точке с соответствующим значением х с положительным направлением оси Ох.
Следовательно, значение производной при данном значении х равно тангенсу угла, образованного касательной к графику функции в точке с соответствующим значением х с положительным направлением оси Ох.
Механический смысл производной.
Рассмотрим прямолинейное движение тела, для которого пройденное расстояние есть функция от времени: s=f(t). Среднюю скорость за время Δt можно определить по формуле:
 . Для определения мгновенной скорости тела в данный момент времени устремим Δt к нулю. Получим:
. Для определения мгновенной скорости тела в данный момент времени устремим Δt к нулю. Получим:  Таким образом, производная от расстояния в данный момент времени равна мгновенной скорости движения в этот момент. Соответственно производная любой функции при данном значении аргумента равна скорости изменения этой функции при рассматриваемом х.
Таким образом, производная от расстояния в данный момент времени равна мгновенной скорости движения в этот момент. Соответственно производная любой функции при данном значении аргумента равна скорости изменения этой функции при рассматриваемом х.
Уравнение касательной к графику функции.
Составим уравнение касательной к графику функции y = f(x) при х = х0. Эта прямая должна проходить через точку с координатами (х0,у0), лежащую на графике функции, где у0 = f(x0), и иметь угловой коэффициент, равный производной f(x) при х = х0. Воспользовавшись уравнением (7.9), получим: у = f`(x0)х + b, причем у0 = f`(x0)x0 + b, то есть b = y0 - f`(x0)x0. Тогда уравнение касательной можно записать в виде:
 или
или 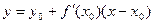 (17.1)
(17.1)
Дифференцируемость функции.
Определение 17.2. Если приращение функции y = f(x) при х = х0 можно представить в виде
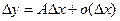 , (17.2)
, (17.2)
где A = const, то y = f(x) называется дифференцируемой при х = х0, а АΔх называется главной линейной частью приращения или дифференциалом функции.
Обозначение: dy = АΔх.
Замечание. Так как при у = х получаем dx = 1·Δx, можно обозначать Δх = dx.
Теорема 17.1. Функция дифференцируема в некоторой точке в том и только в том случае, если она имеет в этой точке производную.
Доказательство.
1) Если для y=f(x) существует  , то
, то  , где β(Δх) – бесконечно малая при Δх→0. Тогда
, где β(Δх) – бесконечно малая при Δх→0. Тогда  . Следовательно, функция y = f(x) дифференцируема при х = х0, причем А = f`(x0).
. Следовательно, функция y = f(x) дифференцируема при х = х0, причем А = f`(x0).
2) Пусть y=f(x) дифференцируема при х=х0, то есть ее приращение имеет вид (17.2). Тогда 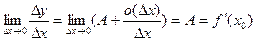 . Таким образом, f(x) имеет производную в точке х0, равную А.
. Таким образом, f(x) имеет производную в точке х0, равную А.
Следствие. Дифференциал функции можно представить в виде  , а производную – в виде
, а производную – в виде  .
.
Теорема 17.2. Если функция дифференцируема в некоторой точке, то она непрерывна в этой точке.
Доказательство. Из формулы (17.2) следует, что , что и означает непрерывность f(x) при х = х0.
, что и означает непрерывность f(x) при х = х0.
Замечание. Обратное утверждение неверно, то есть из непрерывности функции не следует ее дифференцируемость. Например, y = |x| непрерывна при х = 0, но не дифференцируема в этой точке.
Геометрический смысл дифференциала









 у Рассмотрим график функции y=f(x) и проведем
у Рассмотрим график функции y=f(x) и проведем
В касательную к нему при х=х0. Тогда при прира-
щении аргумента Δх приращение функции Δу
С равно длине отрезка BD, а приращение ордина-
ты касательной 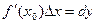 равно длине
равно длине
А D отрезка CD. Следовательно, дифференциал
функции равен приращению ординаты
Δх касательной.
х0 х
Линеаризация функции.
Так как истинное значение приращения функции отличается от ее дифференциала на бесконечно малую более высокого порядка, чем Δх, при приближенных вычислениях можно заменять Δу на dy, то есть считать, что f(x0 + Δx) ≈ f(x0) + dy = f(x0) + f`(x0)(x -x0). При этом функция f(x) для значений х, близких к х0, приближенно заменяется линейной функцией. Эта операция называется линеаризацией функции.
Пример.
Найдем приближенное значение 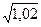 . Пусть
. Пусть 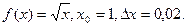 Тогда
Тогда
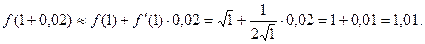
Лекция 18.
Свойства производной (правила дифференцирования). Производная сложной и обратной функций. Инвариантность формы дифференциала. Таблица производных, логарифмическое дифференцирование. Дифференцирование функций, заданных параметрически.
Правила дифференцирования.
Пусть при рассматриваемых значениях х существуют производные функций f(x) и g(x), то есть эти функции являются дифференцируемыми при данных значениях аргумента. Сформулируем и докажем некоторые свойства производных.
1.  (18.1)
(18.1)
Доказательство. 
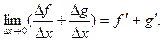
2.  где k=const. (18.2)
где k=const. (18.2)
Доказательство. 
3.  (18.3)
(18.3)
Доказательство. 
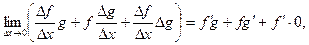 так как
так как 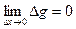 в силу непрерывности g(x).
в силу непрерывности g(x).
4. Если g(x)≠0, то  (18.4)
(18.4)
Доказательство.
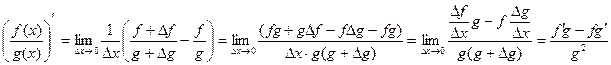
Производная сложной функции.
Если функция u = φ(x) имеет при некотором значении х производную ux΄=φ΄(x), а функция y = f(u) имеет при соответствующем значении u производную yu΄= f΄(u), то сложная функция y = f(φ(x)) тоже имеет при данном значении х производную, равную
y΄(x) = f΄(u)·u΄(x). (18.5)
Доказательство.
Так как  то по третьему определению предела можно представить
то по третьему определению предела можно представить
 где
где  при
при Тогда
Тогда  Разделив обе части равенства на Δх, получим:
Разделив обе части равенства на Δх, получим:
 . Переходя к пределу при Δх→0, получаем:
. Переходя к пределу при Δх→0, получаем:  так как
так как 
Производная обратной функции.
Если для функции y=f(x) существует обратная функция х=φ(у), которая в некоторой точке у имеет производную φ′(у)≠0, то в соответствующей точке х функция f(x) тоже имеет производную, причем  (18.6)
(18.6)
Доказательство.
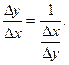 Так как φ(у) непрерывна, Δх→0 при Δу→0, и при переходе к пределу при Δу→0 получаем:
Так как φ(у) непрерывна, Δх→0 при Δу→0, и при переходе к пределу при Δу→0 получаем:  .
.
Инвариантность формы дифференциала.
Найдем выражение для дифференциала сложной функции. Пусть y=f(u), u=φ(x), то есть y=f(φ(x)). Тогда  следовательно,
следовательно,  Но
Но  поэтому
поэтому 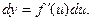 Таким образом, форма дифференциала не зависит от того, является аргумент функции независимой переменной или функцией другого аргумента. Это свойство называется свойством неизменности, или инвариантности, дифференциала.
Таким образом, форма дифференциала не зависит от того, является аргумент функции независимой переменной или функцией другого аргумента. Это свойство называется свойством неизменности, или инвариантности, дифференциала.
Производные основных элементарных функций.
Используя полученные формулы и свойства производных, найдем производные основных элементарных функций.
1. Если f(x)=C=const, то ΔС=0, поэтому С΄=0.
2. у=xn, где n – натуральное число. Тогда по формуле бинома Ньютона можно представить  Следовательно, у΄ = nxn-1.
Следовательно, у΄ = nxn-1.
3. y = sinx, 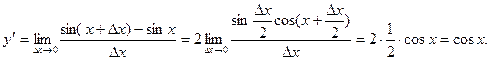
4. y = cosx, 
5. 
6. Аналогично можно получить формулу 
7.  (см. 2-е следствие из второго замечательного предела).
(см. 2-е следствие из второго замечательного предела).
8.  (см. 1-е следствие из второго замечательного предела).
(см. 1-е следствие из второго замечательного предела).
9. 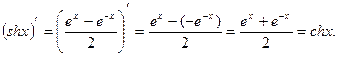 Таким же образом можно найти производные остальных гиперболических функций.
Таким же образом можно найти производные остальных гиперболических функций.
10. По формуле производной обратной функции
 .
.
 .
.
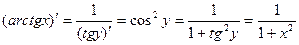 .
.
 .
.
11. Если α – произвольное действительное число, то
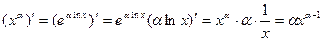 .
.
В результате получена таблица основных производных:
| № | f(x) | f΄(x) | № | f(x) | f΄(x) |
| C | ctgx | 
| |||
| xα | αxα-1 | shx | chx | ||
| ax | axlna | chx | shx | ||
| ex | ex | thx | 
| ||
| lnx | 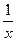
| cthx | 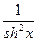
| ||
| sinx | cosx | arcsinx | 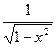
| ||
| cosx | -sinx | arccosx | 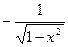
| ||
| tgx | 
| arctgx | 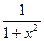
| ||
| arcctgx | 
|
Логарифмическое дифференцирование.
Иногда полезно использовать так называемую формулу логарифмического дифференцирования. Пусть f(x)>0 на некотором множестве значений аргумента и дифференцируема на этом множестве. Тогда по формуле производной сложной функции
 откуда f΄(x)=f(x)(ln f(x))΄. (18.7)
откуда f΄(x)=f(x)(ln f(x))΄. (18.7)
Эту формулу удобно использовать в тех случаях, когда производную натурального логарифма данной функции найти проще, чем производную самой функции.
Примеры.
1. 
2. 
=
Дифференцирование функций, заданных параметрически.
Если функция y = f(x) задана в виде:  , причем функция φ(t) имеет обратную функцию t = Φ(x), то у = ψ(Φ(х)), и
, причем функция φ(t) имеет обратную функцию t = Φ(x), то у = ψ(Φ(х)), и  . (18.7)
. (18.7)
Полученная формула дает возможность находить производную функции, заданной параметрически, без определения непосредственной зависимости у от х.
Пример.
х = а(1 – cos t), y = a(t – sin t) – параметрические уравнения кривой, называемой циклоидой. Найдем у΄(х): х΄(t) = asin t, y΄(t) = a(1-cost),  .
.
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 438; Нарушение авторских прав?; Мы поможем в написании вашей работы!