Лекция 23

Дифференцируемой на отрезке.

Пусть функция y = f(x) дифференцируема на отрезке [ab]. Тогда по теореме 17.2 она непрерывна на нем, и по теореме 16.2 достигает на этом отрезке своего наибольшего и наименьшего значения. Если f(x) имеет на [ab] конечное число критических точек, то ее наибольшее значение будет либо одним из ее максимумов (а именно, наибольшим максимумом), либо будет достигаться в одной из конечных точек отрезка. То же можно сказать и о наименьшем значении. Из сказанного следует, что поиск наибольшего и наименьшего значений дифференцируемой функции на отрезке можно проводить по следующей схеме:

1) найти критические точки функции, принадлежащие данному отрезку;

2) вычислить значения функции в точках а и b, а также в найденных критических точках. Наименьшее из полученных чисел будет наименьшим значением функции на данном отрезке, а наибольшее – ее наибольшим значением на нем.

Пример. Найдем наибольшее и наименьшее значения функции y = x³ + 3 x ² - 9 x –15 на отрезке [-4, 4]. y ′ = 3 x ² + 6 x – 9 = 0 при х = -3 и х =1. При этом обе найденные критические точки принадлежат данному отрезку. Вычислим значения функции при х = -4, х = -3, х = 1 и х =4.

х	-4	-3
у			-20

Таким образом, наибольшее значение функции на рассматриваемом отрезке равно 61 и принимается на его правой границе, а наименьшее равно –20 и достигается в точке минимума внутри отрезка.

Исследование выпуклости функции. Точки перегиба, их нахождение. Асимптоты функций. Общая схема исследования функции и построения ее графика.

Определение 23.1. Кривая называется выпуклой (обращенной выпуклостью вверх) на интервале (ab), если все точки кривой лежат ниже любой ее касательной на этом интервале.

Определение 23.2.. Кривая называется вогнутой (обращенной выпуклостью вниз) на интервале (ab), если все точки кривой лежат выше любой ее касательной на этом интервале.

у

А В С

Например, кривая, изображенная на рисунке, выпукла на интервале (ВС) и вогнута на интервале (АВ).

Теорема 23.1. Если f ′′(x) < 0 во всех точках интервала (ab), то кривая y = f(x) выпукла на этом интервале. Если f ′′(x) > 0 во всех точках интервала (ab), то кривая y = f(x) вогнутаа на этом интервале.

Доказательство. Докажем первое утверждение теоремы. Пусть f ′′(x) < 0 на (ab).

у

а x₀ b

Выберем на интервале (ab) произвольную точку х = х₀ и докажем, что все точки кривой на этом интервале лежат ниже проведенной в точке с абсциссой х₀ касательной, то есть ордината любой точки кривой на рассматриваемом интервале меньше ординаты касательной. Уравнение кривой имеет вид y = f(x), а уравнение касательной при х = х₀:

.

Тогда . Применив теорему Лагранжа, получим: , где с лежит между х и х₀. Применим к первому множителю правой части полученного равенства еще раз теорему Лагранжа: 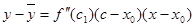(23.1)

(здесь с₁ – между х ₀ и с). Пусть x > x₀. Тогда x₀ < c₁ < c < x, то есть c – x₀ > 0, x – x₀ > 0, f ′′(c₁) < 0, поэтому Если же x < x₀, то x < c < c₁ < x₀, поэтому c – x₀ < 0, x – x₀ < 0, f ′′(c₁) < 0. Но при этом по-прежнему Таким образом, любая точка кривой на данном интервале лежит ниже касательной в точке с абсциссой х₀. Следовательно, кривая является выпуклой.

Второе утверждение теоремы доказывается аналогичным образом.

Определение 23.3. Точка, отделяющая выпуклую часть непрерывной кривой от вогнутой, называется точкой перегиба.

Замечание. Если в точке перегиба существует касательная к кривой, то в этой точке она пересекает кривую, потому что по одну сторону от данной точки кривая проходит выше касательной, а по другую – ниже.

Теорема 23.2 (необходимое условие точки перегиба). Если в точке x₀ перегиба кривой, являющейся графиком функции y = f(x), существует вторая производная f ′′(x), то f ′′(x₀) = 0.

Доказательство. Так как при х = х₀ 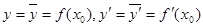, по формуле Тейлора получаем: . Если бы , разность 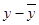сохраняла бы постоянный знак в некоторой окрестности точки х₀, в то время как в точке перегиба эта разность должна менять знак. Следовательно, f ′′(x₀) = 0.

Теорема 23.3 (достаточное условие точек перегиба). Если функция y = f(x) дифференцируема в точке х₀, дважды дифференцируема в проколотой окрестности этой точки и f ′′(x) меняет знак при х = х₀, то х₀ – точка перегиба.

Доказательство. Воспользовавшись формулой (23.1), получим, что знак разности 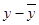определяется знаком f ′′(c₁), так как (c – x₀)(x – x₀) > 0 по обе стороны точки х₀. Следовательно, 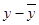меняет знак при х = х₀, то есть х₀ – точка перегиба.

Замечание. Можно доказать, что если в условиях теоремы 22.5 критическая точка не является точкой экстремума, то она является точкой перегиба.

Пример. Найдем интервалы выпуклости и вогнутости и точки перегиба функции y = x³ -6 x² + x – 12. y′ = 3 x ² - 12 x + 1, y′′ = 6 x – 12. y′′ = 0 при х = 2, y′′ < 0 при х < 2, y′′ > 0 при х > 2. Таким образом, график функции является выпуклым при х < 2, вогнутым при х > 2, а х = 2 – точка его перегиба.

Дата добавления: 2014-01-11