
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Предел функции. 4.1. Функции одной переменной
4.1. Функции одной переменной
Определение 1. Пусть X Ì R – некоторое множество, и пусть сформулировано правило f, в силу которого каждому числу  сопоставлено некоторое число y. Тогда будем говорить, что на множестве X определена функция f, или функция f (x), или функция y = f (x) (рис.4).
сопоставлено некоторое число y. Тогда будем говорить, что на множестве X определена функция f, или функция f (x), или функция y = f (x) (рис.4).

Рис. 4.
Понятие, описанное определением 1, представляет собой отображение множе- ства Х в множество R (п.1.2.). Множество X называют областью определения функ- ции f и обозначают через D (f). Число y в определении 1 называют значением функции f в точке x и обозначают через f (x). Совокупность всех значений, принимаемых функцией f в точках множества X, называют множеством значений функции f и обозначают через E (f). В записи y = f (x) букву x называют аргументом или незави- симой переменной, а y – функцией или зависимой переменной.
4.2. Предел функции при x, стремящемся к a, a Î R
Ниже мы рассматриваем функции, областями определения которых являются промежутки или объединения нескольких промежутков. Наиболее часто в качестве об- ласти определения функции выступает окрестность или проколотая окрестность неко- торой точки.
В п. 3.2. окрестностью  точки a, a Î R мы назвали всякий интервал, содер- жащий эту точку. Проколотой окрестностью точки a, a Î R назовем множество, ко- торое получается в результате удаления из окрестности
точки a, a Î R мы назвали всякий интервал, содер- жащий эту точку. Проколотой окрестностью точки a, a Î R назовем множество, ко- торое получается в результате удаления из окрестности  самой точки a. Таким об- разом, если интервал (a; b) является окрестностью точки a (т.е., если a < a < b), то проколотая окрестность этой точки представляет собой объединение интервалов (a; a) и (a; b); обозначать это множество будем символом
самой точки a. Таким об- разом, если интервал (a; b) является окрестностью точки a (т.е., если a < a < b), то проколотая окрестность этой точки представляет собой объединение интервалов (a; a) и (a; b); обозначать это множество будем символом  . Проколотой e-окрестно- стью точки a (a Î R, e > 0) назовем объединение интервалов
. Проколотой e-окрестно- стью точки a (a Î R, e > 0) назовем объединение интервалов 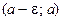 и
и 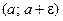 ; обозначать это множество будем символом
; обозначать это множество будем символом 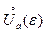 :
:
 .
.
Предел функции принадлежит к начальным понятиям математического анализа. Его определение опирается на понятие сходящейся последовательности. Заметим, что если аргумент x функции f пробегает некоторую числовую последовательность 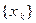 , то значения функции в точках
, то значения функции в точках  образуют числовую последовательность
образуют числовую последовательность  , где
, где 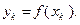
Пусть функция f определена в проколотой окрестности 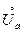 , a Î R, и пусть A – некоторое число. Заметим: в точке а функция может быть определена, а может быть и нет.
, a Î R, и пусть A – некоторое число. Заметим: в точке а функция может быть определена, а может быть и нет.
Определение 1. Число A назовем пределом функции f при x, стремящемся к a, если для всякой последовательности 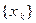 , удовлетворяющей условиям
, удовлетворяющей условиям
1) все члены последовательности содержатся в 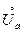 и
и
2) последовательность сходится к а,
соотвеетствующая последовательность 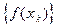 значений функции сходится к A.
значений функции сходится к A.
Будем пользоваться компактной записью условий определения 1:

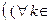 N
N 
Прочесть эту строчку можно так: для всякой последовательности { x k }, лежа- щей в проколотой окрестности точки а и сходящейся к а, соответствующая последо- вательность { f (x k } значений функции сходится к А.
Геометрический смысл определения 1 очевиден: какова бы ни была последова- тельность значений аргумента 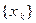 , сходящаяся к a (она изображается последова- тельностью точек на числовой оси, сгущающейся вокруг точки a), соответствующая последовательность
, сходящаяся к a (она изображается последова- тельностью точек на числовой оси, сгущающейся вокруг точки a), соответствующая последовательность 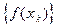 значений функции изображается последовательностью точек, сгущающейся вокруг точки А.
значений функции изображается последовательностью точек, сгущающейся вокруг точки А.
Если число A удовлетворяет условиям определения 1, будем записывать:
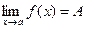 или
или 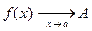 .
.
Пример 1. Покажем, что 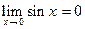 .
.
Начнем с доказательства неравенств, к которым часто будем обращаться в дальнейшем.
Лемма. При всех х 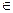
 справедливы неравенства
справедливы неравенства
 (1)
(1)
► Пусть сначала 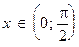 . Рассмотрим круг некоторого радиуса r, и пусть OA и OB – два радиуса этого круга, ограничивающие сектор S с центральным углом x (рис.5.). Треугольник AOB содержится в секторе S, который, в свою очередь, содержится в прямоугольном треугольнике AOC; поэтому площадь D AOB не превышает площади S,
. Рассмотрим круг некоторого радиуса r, и пусть OA и OB – два радиуса этого круга, ограничивающие сектор S с центральным углом x (рис.5.). Треугольник AOB содержится в секторе S, который, в свою очередь, содержится в прямоугольном треугольнике AOC; поэтому площадь D AOB не превышает площади S,
 Рис. 5.
Рис. 5.
|
которая не превосходит площади D AOC, т.е.
 ,
,
где  . Отсюда:
. Отсюда: 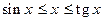 ; а так как все части этиx неравенств неотри- цательны, то можно записать
; а так как все части этиx неравенств неотри- цательны, то можно записать  .
.
Пусть теперь х 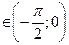 ; тогда t = - x лежит в
; тогда t = - x лежит в 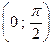 , и по доказанному выше |sin t | ≤ | t |≤ | tg t |. Отсюда, так как sin(- x) = - sin x и tg(- x) = -tgx, получаем для х, при- надлежащих
, и по доказанному выше |sin t | ≤ | t |≤ | tg t |. Отсюда, так как sin(- x) = - sin x и tg(- x) = -tgx, получаем для х, при- надлежащих  :
:  , и утверждения леммы доказаны.◄
, и утверждения леммы доказаны.◄
Перейдем к доказательству равенства 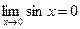 .
.
► Выберем какую-нибудь проколотую окрестность 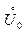 точки 0; например, пусть это будет интервал (–1; 1), из которого удалена точка 0:
точки 0; например, пусть это будет интервал (–1; 1), из которого удалена точка 0: 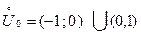 . Пусть
. Пусть 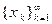 - последовательность такая, что 1) все ее члены содержатся в
- последовательность такая, что 1) все ее члены содержатся в 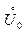 и 2)
и 2) 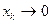 . Таких последовательностей существует бесконечно много, например,
. Таких последовательностей существует бесконечно много, например,  ,
,  и т.п.;
и т.п.; 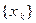 – одна из подобных последовательностей, любая из них. В силу неравенств (1) при всех натуральных k имеем: 0
– одна из подобных последовательностей, любая из них. В силу неравенств (1) при всех натуральных k имеем: 0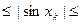
 . Отсюда и из теоремы о “сжатой “ последовательности (теорема 5, п. 3.3.) следует:
. Отсюда и из теоремы о “сжатой “ последовательности (теорема 5, п. 3.3.) следует: 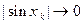 , а тогда и
, а тогда и  . Таким образом, какова бы ни была последовательность
. Таким образом, какова бы ни была последовательность  , удовлетворяющая сформулированным выше условиям 1) и 2), соответствующая последовательность
, удовлетворяющая сформулированным выше условиям 1) и 2), соответствующая последовательность 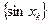 сходится к A = 0; следовательно, в силу определения 1
сходится к A = 0; следовательно, в силу определения 1  ◄
◄
Пример 2. Пусть f (x) = [ x ], где [ x ] есть целая часть числа х, т.е. наиболь- шее из целых чисел, не превосходящих х (если n 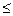 x < n+1, где n
x < n+1, где n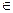 Z, то [ x ]= n). На рис.6. изображен график этой функции. Покажем, что она не имеет предела при х, стремящемся к нулю.
Z, то [ x ]= n). На рис.6. изображен график этой функции. Покажем, что она не имеет предела при х, стремящемся к нулю.
 Рассмотрим какую-нибудь проколотую окрестность точки 0, например, интервал (–1; 1), из которого удалена точка 0. Обозначим
Рассмотрим какую-нибудь проколотую окрестность точки 0, например, интервал (–1; 1), из которого удалена точка 0. Обозначим 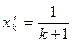 и
и  и рассмотрим б.м. последовательности
и рассмотрим б.м. последовательности 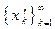 и
и 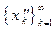 . Каждая из них удовлетво- ряет требованиям 1) и 2) определения 1. Очевидно, при всех натуральных k
. Каждая из них удовлетво- ряет требованиям 1) и 2) определения 1. Очевидно, при всех натуральных k 
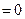 и
и 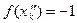 .; поэтому
.; поэтому 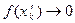 и
и 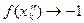 . Таким образом, для указан-ных последовательностей
. Таким образом, для указан-ных последовательностей 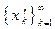 и
и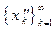 соответствующие им последовательности
соответствующие им последовательности 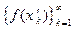 и
и 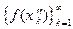 значений функции имеют различные пределы.
значений функции имеют различные пределы.
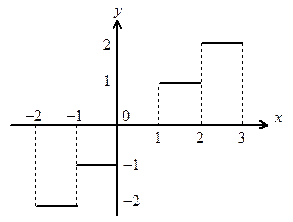 Рис. 6.
Рис. 6.
|
Следовательно, не существует числа A, удовлетворяющего определению 1. 
Приведём еще одно определение предела функции, эквивалентное опреде- лению 1, но сформулированное в других терминах.
Пусть функция f определена в 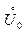 , a Î R, и пусть A – некоторое число.
, a Î R, и пусть A – некоторое число.
Определение 2. Число A называют пределом функции f при x, стремящемся к a, если для любого e > 0 существует d > 0 такое, что при всех x, удовлетворяющих неравенствам 0 <  , справедливо
, справедливо
неравенство 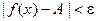 .
.
Запишем условия этого определения, используя логические знаки:
"e > 0 $d > 0: " x Î R 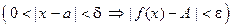 .
.
Прочитать эту строчку можно так: для любого положительного ε существует положительное δ такое, что для всякого вещественного х, удовлетворяющего нера- венствам 0 < | x – a | < δ, соответствующее значение функции f (x) удовлетворяет неравенству | f (x) - A | < ε.
Условия определения 2 можно записать еще и так:
"e > 0 $d > 0 " x Î R  .
.
Геометрический смысл записи  представлен на рис.7:
представлен на рис.7:

Рис. 7.
как только расстояние от х до точки а становится меньше δ, так сразу расстояние между точкой f (x) и точкой A становится меньше e. Существенно, что d, облада- ющее указанным свойствам, существует для любого e, как бы мало оно ни было.
Как уже было сказано выше, определения 1 и 2 эквивалентны, т.е. они описыва- ют одно и то же математическое понятие – предел функции f при x, стремящимся к a. Конечно, их эквивалентность подлежит доказательству; это доказательство можно найти в учебниках [1] и [2].
В дальнейшем определение 1 будем называть определением предела функции на языке последовательностей, а определение 2 – определением предела функции на языке “ e – d”.
Пример 3. На языке ‘ ε- δ’ доказать, что 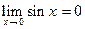 .
.
 Неравенство
Неравенство 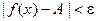 в нашем примере выглядит так:
в нашем примере выглядит так:  . Таким образом, нужно показать, что для любого e > 0 можно подобрать d > 0 такое, что если
. Таким образом, нужно показать, что для любого e > 0 можно подобрать d > 0 такое, что если 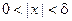 , то
, то  . Согласно неравенствам (1)
. Согласно неравенствам (1) 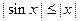 , поэтому если
, поэтому если 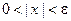 , то
, то  . Следовательно, для всякого e > 0 можно указать d > 0 (например, d = e) такое, что
. Следовательно, для всякого e > 0 можно указать d > 0 (например, d = e) такое, что 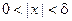 Þ
Þ  ; поэтому
; поэтому 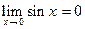 .
. 
4.3. Односторонние пределы
Пусть функция f определена на некотором интервале (a; b) и пусть A – некоторое число.
Определение 1. Число A называют пределом функции f при x, стремящемся к a справа, если для всякой последовательности  такой, что
такой, что
1) все ее члены лежат на (а; b) и
2) она сходится к а, соответствующая последовательность 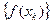 значений функции сходится к А, т.е.
значений функции сходится к А, т.е.

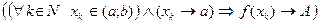 .
.
Это определение сформулировано на языке последовательностей. Сформулируем эквивалентное определение на языке “ ε- δ”
Пусть функция f определена на некотором интервале (a;b) и пусть А – некоторое число..
Определение 1΄. Число А называют пределом функции f при х, стремящемся к а справа, если для любого ε > 0 существует δ > 0 такое, что для всякого х, удов- летворяющего неравенствам а < x < x+δ, соответствующее значение функции f (x) удовлетворяет неравенству | f (x) – A | < ε, т.е.
"e > 0 $d > 0: " x Î R 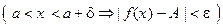 .
.
. Если A есть предел функции f при x, стремящемся к a справа, будем записывать:  или
или 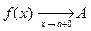 или A = f (a + 0).
или A = f (a + 0).
Определение 2. Число A называют пределом функции f при x, стремящемся к b слева, если (на языке последовательностей)
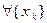
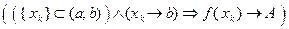 ,
,
или если (на языке “ ε- δ”)
"e > 0 $d > 0: " x Î R  .
.
Если A является пределом функции f при x, стремящимся к b слева, будем применять обозначения:  или
или  или A = f (b – 0).
или A = f (b – 0).
Теорема 1. (О связи предела функции с ее односторонними пределами)
Пусть функция f определена в ,
,  , и пусть A – некоторое число. Для того чтобы A было пределом функции f при
, и пусть A – некоторое число. Для того чтобы A было пределом функции f при 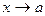 , необходимо и достаточно, чтобы A было односторонним пределом функции f как при х, стремящемся к а справа, так и при х, стремящемся к а слева..
, необходимо и достаточно, чтобы A было односторонним пределом функции f как при х, стремящемся к а справа, так и при х, стремящемся к а слева..
 Необходимость. Пусть
Необходимость. Пусть 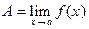 . Зададим
. Зададим  ; найдется
; найдется 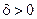 такое, что
такое, что 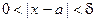 Þ
Þ  , а это означает, что справедливы два утверждения:
, а это означает, что справедливы два утверждения:
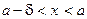 Þ
Þ  ; (2)
; (2)
 Þ
Þ  . (3)
. (3)
Так как  было задано произвольно, то из (2) следует:
было задано произвольно, то из (2) следует:
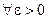
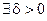 :
: 
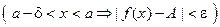 ,
,
т.е.  . Из (3) аналогично следует:
. Из (3) аналогично следует: 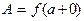 .
.
Достаточность. Пусть  . Зададим
. Зададим  . Так как
. Так как  , найдется
, найдется 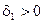 такое, что
такое, что 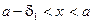 Þ
Þ  . Так как
. Так как 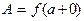 , найдется
, найдется  такое, что
такое, что 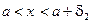 Þ
Þ  . Обозначим:
. Обозначим: 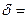
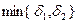 . Заметим: если х удовлетворяет неравенствам 0 < | x - a | < δ, то для него справедливо либо
. Заметим: если х удовлетворяет неравенствам 0 < | x - a | < δ, то для него справедливо либо 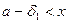 < < а, либо
< < а, либо  . И в том, и в другом случае выполняется
. И в том, и в другом случае выполняется  . Таким образом, 0 < | x - a | < δ Þ
. Таким образом, 0 < | x - a | < δ Þ  . Но
. Но  было задано произвольно. Значит,
было задано произвольно. Значит,
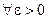
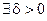 :
: 
 ,
,
поэтому 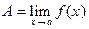 .
. 
Упражнение. Для функции f примера 2, п. 4.2, показать, что 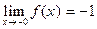 ;
;  (
( пишут вместо x → 0 - 0; х → +0 пишут вместо
пишут вместо x → 0 - 0; х → +0 пишут вместо 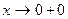 ).
).
4.4. Предел функции на бесконечности
Пусть функция f определена на интервале  , где
, где  , и пусть A – некоторое число.
, и пусть A – некоторое число.
Определение 1. Число A называют пределом функции f при x, стремящем- ся к +¥, если для всякой последовательности 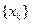 , удовлетворяющей условиям
, удовлетворяющей условиям
1) все члены последовательности содержатся в интервале (а;+∞) и
2) х  , соответствующая ей последовательность
, соответствующая ей последовательность 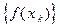 значений функции сходится к A, т.е. если΄
значений функции сходится к A, т.е. если΄

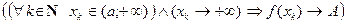 .
.
Это определение сформулировано на языке последовательностей. Приведем формулировку эквивалентного определения на языке “ ε – δ”
Пусть функция f определена на интервале (а;+∞), где а 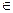 R, и пусть А - некоторое число.
R, и пусть А - некоторое число.
Определение 1′. Число А называют пределом функции f при х, стремящемся к +∞, если для любого ε > 0 существует Δ > 0 такое, что для всякого х, удовлетво- ряющего неравенству x > Δ, соответствующее значение функции f (x) удовлетворяет неравенству 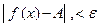 , т.е. если
, т.е. если
 R
R 
Если число A удовлетворяет условиям одного из этих определений, будем записывать 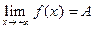 , или
, или  , или
, или 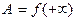 .
.
Пусть функция f определена на интервале 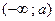 , где
, где  , и пусть A – некоторое число.
, и пусть A – некоторое число.
Определение 2. Число A называют пределом функции f при x, стремящемся к 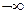 , если (на языке последовательностей)
, если (на языке последовательностей)

 ,
,
или если (на языке “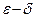 ”)
”)
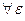 > 0
> 0  R
R 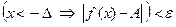 .
.
Если число A удовлетворяет условиям определения 2, будем записывать
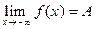 , или
, или 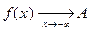 , или
, или 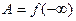 .
.
Пусть a и b – некоторые числа,  . Объединение интервалов
. Объединение интервалов  и
и 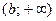 будем называть проколотой окрестностью бесконечности и обозначать символом
будем называть проколотой окрестностью бесконечности и обозначать символом 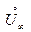 :
:  .
.
Определение 3. Пусть функция f определена в 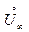 и пусть A – некоторое число. Число A называют пределом функции f при x, стремящемся к ¥, если
и пусть A – некоторое число. Число A называют пределом функции f при x, стремящемся к ¥, если
(на языке последовательностей)

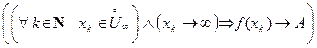 ,
,
или если (на языке “ε−δ”)
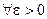
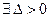 :
: 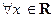
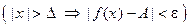 .
.
Если число A удовлетворяет условиям этого определения, будем записывать
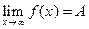 , или
, или  , или A = f (¥).
, или A = f (¥).
Пример 1. Пусть 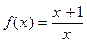 . Этим равенством f определена при всех
. Этим равенством f определена при всех  , т.е. она определена в проколотой окрестности бесконечности
, т.е. она определена в проколотой окрестности бесконечности 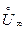 = (-∞;0)
= (-∞;0)  (0;+∞). Покажем, что
(0;+∞). Покажем, что 
 Докажем равенство
Докажем равенство 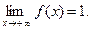 Пусть
Пусть 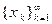 – некоторая последова- тельность, такая, что 1) при всех k
– некоторая последова- тельность, такая, что 1) при всех k 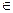 N
N 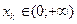 и 2)
и 2)  . Заметим:
. Заметим: 
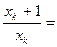
 , причем
, причем 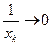 , так как х
, так как х 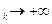 (п. 3.4., теорема 1). Значит, f (x
(п. 3.4., теорема 1). Значит, f (x 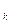 )→1. Здесь
)→1. Здесь  - произвольная последовательность, удовлетворяющая условиям 1) и 2). Следователь- но, число 1 удовлетворяет определению 1. Доказательства равенств
- произвольная последовательность, удовлетворяющая условиям 1) и 2). Следователь- но, число 1 удовлетворяет определению 1. Доказательства равенств  и
и 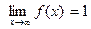 аналогичны.
аналогичны. 
В рассмотренном примере все три предела одинаковы. Это не случайно, ибо справедлива теорема, аналогичная теореме 1, п.4.3.
Теорема 1. (О связи предела функции при х→∞ с ее пределами при х→ + ∞ и при → -∞) Пусть функция f определена в 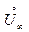 , и пусть A – некоторое число. Для того чтобы A было пределом f при
, и пусть A – некоторое число. Для того чтобы A было пределом f при 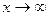 , необходимо и достаточно, чтобы A было пределом f как при
, необходимо и достаточно, чтобы A было пределом f как при 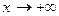 , так и при
, так и при 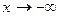 .
.
► Необходимость. Пусть А =  . Зaдадим некоторое ε > 0. В силу определения 3. найдется Δ > 0 такое, что для всякого вещественного х, удовлетво- ряющего неравенству │ х │> Δ справедливо │ f (x) – A │< ε. В частности, последнее неравенство справедливо при х > Δ: х > Δ ═›| f (x) – A | < ε.
. Зaдадим некоторое ε > 0. В силу определения 3. найдется Δ > 0 такое, что для всякого вещественного х, удовлетво- ряющего неравенству │ х │> Δ справедливо │ f (x) – A │< ε. В частности, последнее неравенство справедливо при х > Δ: х > Δ ═›| f (x) – A | < ε.
Здесь положительное ε было задано произвольно, так что можем записать:
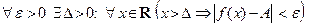
В силу определения 1 это означает:  Доказательство равенства
Доказательство равенства  проводится аналогично.
проводится аналогично.
Достаточность. Пусть 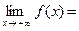
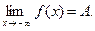 Зададим некоторое ε>0. Так как
Зададим некоторое ε>0. Так как  , в силу определения 1 существует Δ1> 0 такое, что при всех х > Δ1 справедливо | f (x) – A | < ε. Так как
, в силу определения 1 существует Δ1> 0 такое, что при всех х > Δ1 справедливо | f (x) – A | < ε. Так как 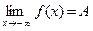 , в силу определения 2 су- ществует Δ2 >0 такое, что при всех х <- Δ2 справедливо не равенство | f(x) – A| < ε. Обозначим: Δ = max { Δ1, Δ2 }. Если х удовлетворяет неравенству | х| > Δ, то для него справедливо либо х > Δ1, либо х <- Δ2. И в том, и в другом случае выполняется
, в силу определения 2 су- ществует Δ2 >0 такое, что при всех х <- Δ2 справедливо не равенство | f(x) – A| < ε. Обозначим: Δ = max { Δ1, Δ2 }. Если х удовлетворяет неравенству | х| > Δ, то для него справедливо либо х > Δ1, либо х <- Δ2. И в том, и в другом случае выполняется  . Таким образом, | х| > Δ Þ
. Таким образом, | х| > Δ Þ  . Но
. Но  было задано произ- вольным. Значит,
было задано произ- вольным. Значит,
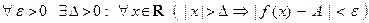
В силу определения 3. это означает: 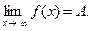 ◄
◄
Пример 2. Доказать: 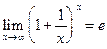 (число e было введено в п. 3.6.).
(число e было введено в п. 3.6.).
► Заметим, что степень 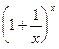 определена для тех x, при которых
определена для тех x, при которых 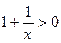 , т.е. при
, т.е. при  и
и  . Таким образом, функция
. Таким образом, функция  определена в
определена в 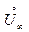 = (-∞;-2)
= (-∞;-2) . Из теоремы 1 следует, что достаточно доказать равенства
. Из теоремы 1 следует, что достаточно доказать равенства  и
и  .
.
*) Докажем, что  .
.
Пусть 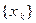 – последовательность такая, что 1)
– последовательность такая, что 1) 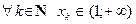 и 2) х
и 2) х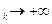 . Обозначим через
. Обозначим через 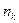 целую часть числа
целую часть числа  , т.е.
, т.е.  - натуральное число такое, что
- натуральное число такое, что 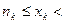
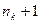 . Из этих неравенств для х k следует:
. Из этих неравенств для х k следует:
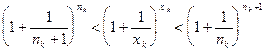 (4)
(4)
Так как  , то и
, то и 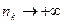 ; поэтому из равенства
; поэтому из равенства 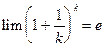 (см. п. 3.6., Следствие) следует:
(см. п. 3.6., Следствие) следует:
 ;
;  .
.
Отсюда: 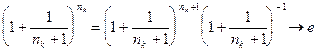 ,
,
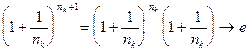 .
.
Теперь из (4) и теоремы о “сжатой“ последовательности (п.3.3. теорема 5) следует: 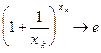 , т.е.
, т.е. 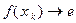 . Здесь
. Здесь 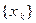 – произвольная последовательность, удовлетворяющая указанным выше условиям 1) и 2), так что
– произвольная последовательность, удовлетворяющая указанным выше условиям 1) и 2), так что

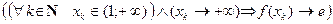 .
.
В силу определения 1  .
.
**) Докажем равенство  .
.
Пусть 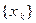 – некоторая последовательность такая, что
– некоторая последовательность такая, что
1) 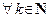
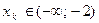 , и 2)
, и 2)  . Обозначим:
. Обозначим:  . Очевидно,
. Очевидно, 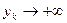 , и по доказанному в *)
, и по доказанному в *) 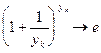 . Справедливы равенства:
. Справедливы равенства:
 .
.
Отсюда: 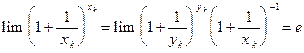 , и равенство
, и равенство 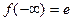 доказано.
доказано.
Теперь из *), **) и теоремы 1 следует 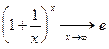 .
. 
4.5. Некоторые теоремы о пределах
Теоремы этого пункта аналогичны теоремам из п.3.3.
Теорема 1. (О единственности предела) Пусть функция f определена в проколотой окрестности  ,
, 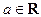 . Если предел функции f при x, стремящемся к a существует, то только один.
. Если предел функции f при x, стремящемся к a существует, то только один.
 Предположим, что нашлись два различных числа A и B, каждое из кото- рых является пределом функции f при x, стремящемся к а. Пусть
Предположим, что нашлись два различных числа A и B, каждое из кото- рых является пределом функции f при x, стремящемся к а. Пусть 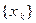 – некоторая последовательность такая, что 1) все ее члены содержатся в
– некоторая последовательность такая, что 1) все ее члены содержатся в  и 2)
и 2) 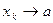 . В си- лу определения 1, п.4.2., последовательность значений функции
. В си- лу определения 1, п.4.2., последовательность значений функции 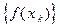 должна сходиться и к числу A, и к числу B, а это противоречит теореме о единственности предела последовательности
должна сходиться и к числу A, и к числу B, а это противоречит теореме о единственности предела последовательности 
Теорема 2. (О стабилизации знака неравенства) Пусть 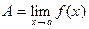 . а p – некоторое число,
. а p – некоторое число,  (
(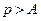 ). Тогда существует
). Тогда существует  такое, что при всех
такое, что при всех  , справедливо неравенство
, справедливо неравенство 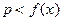
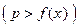 .
.
 Пусть
Пусть  . Положим
. Положим 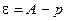 . В силу определения 1',п. 4.2., найдется
. В силу определения 1',п. 4.2., найдется  такое, что при всех
такое, что при всех  справедливо неравенство
справедливо неравенство  , кото- рое эквивалентно неравенствам
, кото- рое эквивалентно неравенствам  . Но
. Но 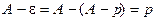 . Значит, при всех
. Значит, при всех  справедливо
справедливо 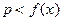 , что и требовалось доказать. Доказательство теоремы в случае
, что и требовалось доказать. Доказательство теоремы в случае 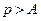 аналогично.
аналогично. 
Теорема 3. (О предельном переходе в неравенстве) Пусть функции f и g определены в ,
, 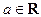 и пусть
и пусть 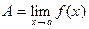 ,
, 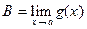 . Если при всех
. Если при всех 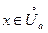 имеет место
имеет место 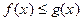 (f (x) ≥ g (x)), то и
(f (x) ≥ g (x)), то и 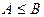 (A≥ B)..
(A≥ B)..
 Пусть
Пусть 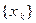 – некоторая последовательность такая, что 1) все ее члены содер- жат ся в
– некоторая последовательность такая, что 1) все ее члены содер- жат ся в  и 2)
и 2) 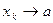 . Рассмотрим последовательности
. Рассмотрим последовательности 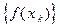 и
и 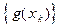 . Так как при всех
. Так как при всех 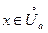 имеет место
имеет место 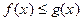 (f (x) ≥ g (x)),, то
(f (x) ≥ g (x)),, то 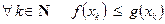 (f (xk) ≥ g(xk)) В силу теоремы 4., п.3.3., отсюда следует
(f (xk) ≥ g(xk)) В силу теоремы 4., п.3.3., отсюда следует 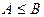 (A≥ B).
(A≥ B). 
Следствие. Пусть f определена в и пусть при всех х
и пусть при всех х 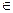
 справедливо
справедливо 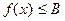 (f (x)
(f (x)  B), где В - некоторое число. Если
B), где В - некоторое число. Если 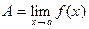 . то
. то 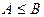 (
(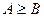 ).
).
► Введем в рассмотрение функцию g, тождественно в  равную В, т.е. для всех
равную В, т.е. для всех 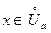 g (x) = B. Очевидно,
g (x) = B. Очевидно,  Можем записать: при
Можем записать: при 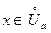 справед- ливо f (x) ≤ ≤g(x) (f (x) ≥ g (x)) В силу теоремы 3 А ≤ В (A ≥ B). ◄
справед- ливо f (x) ≤ ≤g(x) (f (x) ≥ g (x)) В силу теоремы 3 А ≤ В (A ≥ B). ◄
Замечание 1. Если при всех 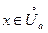 имеет место строгое неравенство
имеет место строгое неравенство 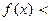
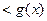 (f (x) > g (x)), то,вообще говоря, для пределов A и B отсюда не следует строгое неравенство А< В (A > B), т.е. возможно равенство А = В. Действительно, если
(f (x) > g (x)), то,вообще говоря, для пределов A и B отсюда не следует строгое неравенство А< В (A > B), т.е. возможно равенство А = В. Действительно, если  , а
, а  , то при
, то при 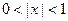 имеем
имеем 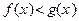 . Таким образом, в проколотой окрестности точки 0
. Таким образом, в проколотой окрестности точки 0 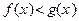 , но
, но  .
.
Теорема 4. (О “ сжатой“ функции) Пусть функции f, g и h определены в и удовлетворяют требованиям
и удовлетворяют требованиям
:1) при всех 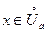
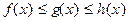 и 2)
и 2)  ,
,  . Тогда функция g имеет предел при
. Тогда функция g имеет предел при 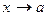 , причем
, причем 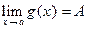 .
.
 Пусть
Пусть 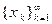 – некоторая последовательность такая, что 1) все ее чле- ны содержатся в
– некоторая последовательность такая, что 1) все ее чле- ны содержатся в  и 2)
и 2) 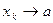 . Из условий теоремы вытекает:
. Из условий теоремы вытекает: 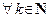
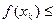

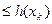 и
и 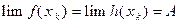 . Отсюда и из теоремы 5,п.3.3., получим:
. Отсюда и из теоремы 5,п.3.3., получим:  . Так как
. Так как 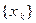 – произвольная последовательность, удовлетворяющая условиям 1) и 2), то в силу определения 1, п.4.2.,
– произвольная последовательность, удовлетворяющая условиям 1) и 2), то в силу определения 1, п.4.2., 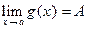 .
. 
Теорема 5. (Об арифметических действиях с пределами) Пусть функции f и g определены в и пусть
и пусть 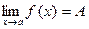 ,
, 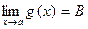 . Тогда
. Тогда
а)  ;
;
б)  ;
;
в) если 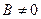 , то
, то 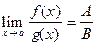 .
.
 Докажем сначала утверждения а) и б). Пусть
Докажем сначала утверждения а) и б). Пусть 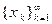 – произвольная после- довательность такая, что 1) все ее члены содержатся в
– произвольная после- довательность такая, что 1) все ее члены содержатся в  и 2)
и 2) 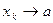 . В силу условий теоремы
. В силу условий теоремы 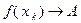 и
и  , а тогда
, а тогда 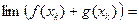 А+В и
А+В и 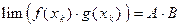 . Так как
. Так как 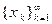 – произвольная последовательность, удовлетворяющая условиям 1) и 2), то из определения 1, п. 4.2., следуют равенства а) и б).
– произвольная последовательность, удовлетворяющая условиям 1) и 2), то из определения 1, п. 4.2., следуют равенства а) и б).
Докажем утверждение в). Будем считать для определенности, что 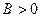 . Пусть p – некоторое число, для которого выполнены условия
. Пусть p – некоторое число, для которого выполнены условия 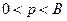 . Согласно теореме 2 найдется
. Согласно теореме 2 найдется  такое, что при всех
такое, что при всех 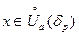 справедливо
справедливо 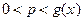 . Значит, если
. Значит, если 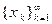 – произвольная последовательность такая, что 1) все ее члены содер- жатся в
– произвольная последовательность такая, что 1) все ее члены содер- жатся в  и 2)
и 2) 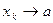 , то все члены последовательности
, то все члены последовательности 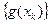 отличны от нуля, и потому можно опереться на утверждение в) теоремы 1, п. 3.5:
отличны от нуля, и потому можно опереться на утверждение в) теоремы 1, п. 3.5: 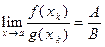 . В силу определения 1, п. 4.2., отсюда следует:
. В силу определения 1, п. 4.2., отсюда следует: 

Замечание 2. Теоремы, аналогичные теоремам этого параграфа, справедливы и для пределов при x, стремящемся к 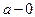 и
и 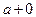 (
(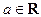 ), а также к +¥, –¥ и ¥.
), а также к +¥, –¥ и ¥.
Упражнение. Сформулировать и доказать теоремы, аналогичные теоремам этого параграфа для случаев, когда x стремится к 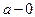 ,
, 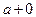 (
(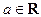 ), +¥, –¥ и ¥.
), +¥, –¥ и ¥.
4.6. Бесконечно малые функции
Определение 1. Функцию a называют бесконечно малой функцией при x, стремящемся к a, а 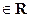 , (б.м. функцией при х → а), если она определена в
, (б.м. функцией при х → а), если она определена в  и если
и если 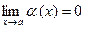 .
.
Аналогичны определения функций, бесконечно малых при x, стремящемся к 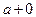 , к
, к 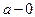 , а также к +¥, к –¥, к ¥.
, а также к +¥, к –¥, к ¥.
Пример 1.  является б.м. функцией при х → 0 (п.4.2., пример 1).
является б.м. функцией при х → 0 (п.4.2., пример 1).
Пример 2. Пусть а, C и m – заданные вещественные числа, причем  и
и  . Степень
. Степень  определена, если ее основание положительно, т.е. при
определена, если ее основание положительно, т.е. при 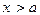 . Положим
. Положим 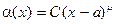 и покажем, что
и покажем, что  является б.м. функцией при
является б.м. функцией при 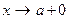 .
.
 Нужно доказать:
Нужно доказать:
: 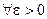
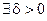 :
: 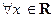
 .
.
Пусть задано  . Рассмотрим неравенство
. Рассмотрим неравенство 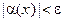 , т.е.
, т.е. 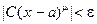 . При
. При 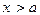 оно равносильно неравенству
оно равносильно неравенству  , поэтому, если положить
, поэтому, если положить 
 , то можем записать:
, то можем записать: 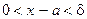 Þ
Þ  .Так как здесь e - произ- вольное положительное число, то мы установили: для любого ε>0 существует δ > 0 (например, δ =
.Так как здесь e - произ- вольное положительное число, то мы установили: для любого ε>0 существует δ > 0 (например, δ =  ) такое, что для всякого х, удовлетворяющего неравенствам 0 < х – a < δ справедливо | α; (x) | < ε. Тем самым равенство
) такое, что для всякого х, удовлетворяющего неравенствам 0 < х – a < δ справедливо | α; (x) | < ε. Тем самым равенство 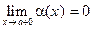 доказано.
доказано. 
Замечание 1 Для некоторых m > 0 степень  определена и при х < a (например, для μ
определена и при х < a (например, для μ 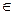 N). Для таких μ
N). Для таких μ 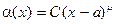 является б.м. функцией при
является б.м. функцией при 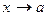 . Доказательство аналогично приведенному выше.
. Доказательство аналогично приведенному выше.
Пример 3. Пусть C и m – заданные вещественные числа, причем  и
и  . Функция
. Функция 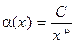 является б.м. функцией при
является б.м. функцией при 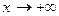 .
.

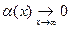 означает:
означает: 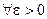
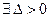
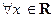
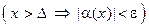 .
.
Пусть задано  . Рассмотрим неравенство
. Рассмотрим неравенство  , т.е.
, т.е.  . При
. При  оно равносильно неравенству
оно равносильно неравенству  , поэтому, если положить
, поэтому, если положить  , то при
, то при 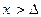 справедливо
справедливо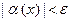 , таким образом,
, таким образом, 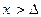 Þ
Þ 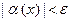 .Так как здесь e – произвольное положительное число, то равенство
.Так как здесь e – произвольное положительное число, то равенство 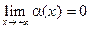 доказано.
доказано. 
Замечание 2. Если показатель m > 0 таков, что степень 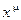 определена и при
определена и при 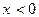 (например,
(например, 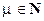 ), то
), то 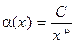 является функцией, бесконечно малой при
является функцией, бесконечно малой при 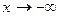 и при
и при 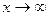 . Доказательство аналогично приведенному выше.
. Доказательство аналогично приведенному выше.
Для б.м. функций справедливы утверждения, аналогичные теоремам о б.м. последовательностях из п.3.4.: сумма б.м. функций есть б.м. функция, произведение ограниченной функции на б.м. функцию есть б.м. функция; справедлива и теорема, аналогичная теореме 3.
Теорема 1. (О разности между функцией и числом) Пусть функция f определена в  ,
, 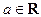 , и пусть А – заданное число. Положим
, и пусть А – заданное число. Положим 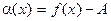 . Чтобы А было пределом f(x) при х, стремящемся к а, необходимо и достаточно, чтобы α (х) была б.м. функцией при
. Чтобы А было пределом f(x) при х, стремящемся к а, необходимо и достаточно, чтобы α (х) была б.м. функцией при 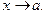
 Пусть
Пусть 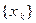 –последовательность такая, что 1)
–последовательность такая, что 1) 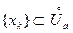 и 2)
и 2) 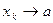 . Рассмотрим последовательности
. Рассмотрим последовательности 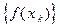 и
и 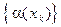 . Так как
. Так как  , то по теореме 3, п.3.4.
, то по теореме 3, п.3.4. 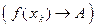 Û
Û  .
.
Пусть 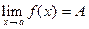 . Тогда
. Тогда  для всякой последовательности
для всякой последовательности 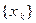 , удовлетворяющей условиям 1) и 2); следовательно, для всякой такой последовательно- сти
, удовлетворяющей условиям 1) и 2); следовательно, для всякой такой последовательно- сти 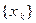 выполняется
выполняется 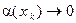 , а это означает, что
, а это означает, что 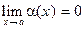 , т.е.
, т.е.
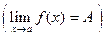 Þ
Þ 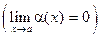 . Аналогично можно доказать обратное утверждение:
. Аналогично можно доказать обратное утверждение: 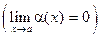 Þ
Þ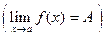 .
.
4.7.. Бесконечно большие функции
Пусть функция a определена в  ,
, 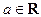 .
.
Определение 1. Будем говорить, что при х, стремящемся к а, функция a стремится к +¥ (к –¥, к ¥), если для любой последовательности 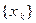 , удовлет- воряющей условиям 1)
, удовлет- воряющей условиям 1) 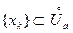 и 2)
и 2) 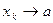 , последовательность
, последовательность 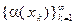 значений функции стремится к +¥ (к –¥, к ¥) соответственно, т.е. если
значений функции стремится к +¥ (к –¥, к ¥) соответственно, т.е. если
