Вертикальный круг теодолита. Место нуля. Измерение углов наклона

Вертикальный круг теодолита служит для определения углов наклона линий 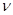или зенитных расстояний z.

Угол наклона называют углом в вертикальной плоскости между горизонтальной линией и визирным лучом, направленным на наблюдаемую точку.

Зенитным расстоянием z называют угол в вертикальной плоскости между отвесной линией и визирным лучом, направленным на наблюдаемую точку. Зенитное расстояние дополняет угол наклона до 90⁰:

z = 90⁰ -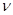

Измерение вертикальных углов начинают с установки прибора в рабочее положение. Установив прибор в рабочее положение, зрительную трубу при КЛ наводят на наблюдаемую точку. Приводят пузырек уровня в нуль-пункт, берут отсчеты и вычисляют из них среднее арифметическое. Затем трубу переводят через зенит, и все действия повторяют при КП. Значение угла получают по формуле 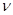= (КП - КЛ) /2. Правильность измерения вертикальных углов контролируется постоянством МО, колебания которого в процессе измерений не должны превышать двойной точности отсчетного устройства.

Перед взятием отсчета по вертикальному кругу у теодолитов, имеющих уровень при алидаде вертикального круга, например, Т15, ТН и т.д., пузырек уровня с помощью установочного винта алидады вертикального круга приводят в ноль-пункт и тем самым обеспечивают неизменность положения отсчетного устройства вертикального круга в момент взятия отсчетов.

У теодолитов, имеющих индекс К, отсчетное устройство вертикального круга приводится в исходное положение автоматически с помощью компенсатора.

Для получения величины угла наклона визирной оси по вертикальному кругу теодолита необходимо знать место нуля вертикального круга, обозначаемое символом МО, или место зенита, обозначаемое МZ.

Измерение вертикальных углов производится при помощи вертикального круга теодолита. Лимб вертикального круга 1 жестко скреплен с осью трубы и вращается вместе с ней. Алидада 2 расположена на оси вращения трубы, но не скреплена с ней и при вращении трубы остается неподвижной. Алидада имеет два верньера 3 и 4 и снабжена цилиндрическим уровнем 5 для приведения линии нулей верньера в определенное положение относительно горизонта. Приведение пузырька уровня в нуль-пункт осуществляют установочным винтом 6 алидады вертикального круга. В теодолите Т30 уровень при алидаде вертикального круга отсутствует. В технических теодолитах вертикальный круг разделен полностью с оцифровкой от 0⁰ до 360⁰. Диаметр 0-180⁰ располагается параллельно визирной оси трубы, вместе с которой он вращается. Для удобства вычисления вертикальных углов: когда визирная ось зрительной трубы и ось уровня при алидаде горизонтальны, нулевые деления алидады должны совпадать с нулевыми делениями вертикального круга. В действительности это условие нарушается, и визирная ось трубы может занимать горизонтальное положение, пузырек находится на середине трубки, а отсчет по вертикальному кругу не равен нулю.

Местом нуля МО называют отсчет по вертикальному кругу теодолита при горизонтальном положении визирной оси трубы, и исходном положении отсчетного устройства. (Отсчет по вертикальному кругу, когда визирная ось трубы горизонтальна, а пузырек уровня при алидаде находится в нуль-пункте, называется местом нуля вертикального круга и обозначается МО).

Местом зенита МZ называют отсчет по вертикальному кругу теодолита при положении визирной оси трубы, направленной в зенит, и исходном положении отсчетного устройства.

При хорошо отъюстированном приборе место нуля МО и место зенита МZ должны быть близки к 0⁰. Но практически значения МО и МZ отличаются от 0⁰ на некоторую величину, которую необходимо учитывать при определении углов наклона 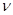или зенитных расстояний z.

Для удобства расчетов МО приводят к значению, близкому к нулю, с положительным или отрицательным знаком, например МО= +0^о01' или МО = - 0^о02'.

Принято считать углы наклона повышения положительными, а углы наклона понижения – отрицательными.

Для измерения вертикальных углов и определения места нуля необходимо прежде всего установить: какое основное положение имеет вертикальный круг теодолита – «лево» (Л) или «право» (П). Основным положением вертикального круга теодолита является то, при котором получают малый положительный (меньше 90⁰) отсчет угла наклона повышения.

Расчетные формулы по определению места нуля и вертикальных углов приводятся в паспортах приборов и зависят от типа оцифровки и основного положения вертикального круга – «круг лево» (КЛ) или «круг право» (КП).

Если основным типом вертикального круга теодолита является «круг лево» (КЛ), а лимб оцифрован против хода часовой стрелки (например, теодолит Т30), то для определения места нуля МО и углов наклона 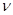используют следующие расчетные формулы:

МО = ; ;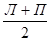

; .

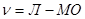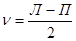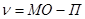Следует иметь в виду, что во все формулы для определения МО и 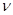вводят отсчеты, имеющие значения более 90⁰, приведенные к малым преобразованным Л или П по следующим правилам:

;

;

.

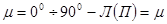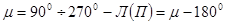
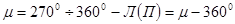Вычисления 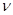обычно ведут по одной из формул, а остальные используют для контроля. Теодолит Т30 имеет штриховой отсчетный микроскоп, а вертикальный круг имеет оцифровку от 0 до 360⁰.

Рассмотрим, как измеряются углы наклона.

Зрительную трубу при КП наводят на некоторую точку М и после приведения пузырька уровня на середину трубки берут отсчет R по вертикальному кругу. Этот отсчет будет больше угла наклона 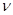на величину МО.

Следовательно, 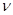= R – МО.

Аналогичные действия выполняют при КЛ. Отсчет Л, также будет увеличен на величину МО. Угол 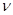= 360 – Л + МО,

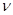= МО – Л.

тогда, МО = (П + Л) /2

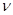= (П – Л) /2

Пример. Пусть отсчет по вертикальному кругу при положении КЛ равен Л=3⁰27', а при КП - П = 356⁰23' – 360⁰ = - 3⁰37', тогда

МО = 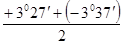= - 0⁰05';

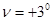27' – (- 0⁰05') = + 3⁰ 32'

контроль:

;

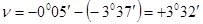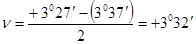
Приведение МО вертикального круга к 0⁰

Для выполнения этого условия несколько раз определяют значение места нуля путем наведения горизонтальной нити сетки зрительной трубы на ряд точек при двух положениях вертикального круга. Если вычисленное по формуле МО = (П + Л) /2 значение места нуля превышает двойную точность отсчетного устройства, то его нужно уменьшить следующим образом. С помощью установочного винта при алидаде вертикального круга устанавливают пузырек уровня на середину. Действуя установочным винтом трубы, ставят на вертикальном круге отсчет, равный среднему вычисленному значению места нуля.

Визирная ось трубы в этом случае будет занимать горизонтальное положение. Теперь необходимо так повернуть алидаду, чтобы при горизонтальном положении оси уровня и визирной оси трубы отсчет был равен 0⁰. Для этого установочным винтом алидады совмещают нули отсчетного приспособления и вертикального круга (пузырек уровня, естественно, сместится с середины). Действуя исправительными винтами уровня, пузырек приводят на середину. Для контроля поверка повторяется.

Дата добавления: 2014-01-11