
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Оцінка параметрів нелінійних функцій
|
|
|
|
При оцінці параметрів нелінійних моделей частіш проводять їх до лінійного вигляду шляхом логарифмування або заміни змінних, а потім використовують МНК.
Розглянемо порядок побудови нелінійної моделі на прикладі степеневої функції (рис. B) 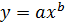 . За допомогою перетворювача (наприклад, логарифмічного підсилювача) одержимо
. За допомогою перетворювача (наприклад, логарифмічного підсилювача) одержимо 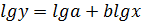 , тобто лінійну залежність відносно логарифмів змінних. Її стає краще видно, якщо провести заміну: Y=lg y; X=lg x; A=lg a. Тоді маємо Y=A+bX і за МНК, згідно формул 6а, 10 знаходимо:
, тобто лінійну залежність відносно логарифмів змінних. Її стає краще видно, якщо провести заміну: Y=lg y; X=lg x; A=lg a. Тоді маємо Y=A+bX і за МНК, згідно формул 6а, 10 знаходимо:
 ; Y=A+bX.
; Y=A+bX.
Ми знайшли оцінки параметрів відносно логарифмів змінних, а для знаходження оцінок 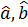 необхідно зробить обернене перетворювання (потенціювання):
необхідно зробить обернене перетворювання (потенціювання):  , тоді
, тоді 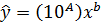 .
.
При таких перетвореннях треба бути уважними, так як критерії значущості та інтервальні оцінки параметрів для нормальної лінійної регресії потребують нормального закону розподілу логарифма вектора збурення, а не самого вектора.
При побудові моделі, що задана в вигляді 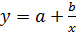 (рис. С) перетворення за допомогою логарифмування неможливе, тому проводять заміну змінних
(рис. С) перетворення за допомогою логарифмування неможливе, тому проводять заміну змінних 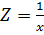 , тоді
, тоді 
В подальшому рахуємо:
Модельні значення  для відповідних значень хі, що подаються із вхідного масиву даних через ответвитель. За допомогою пристрою порівняння рахуємо складові вектора збурення
для відповідних значень хі, що подаються із вхідного масиву даних через ответвитель. За допомогою пристрою порівняння рахуємо складові вектора збурення 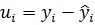 , використовуючи значення уі також із вхідного масиву даних. На основі аналізу вектора збурення оцінюється якість побудованої моделі і, за відповідними критеріями, приймається рішення про здатність моделі до прогнозування.
, використовуючи значення уі також із вхідного масиву даних. На основі аналізу вектора збурення оцінюється якість побудованої моделі і, за відповідними критеріями, приймається рішення про здатність моделі до прогнозування.
Матеріал, що необхідно повторити для вивчення лекції:
1) Знаходження екстремуму функції декількох змінних.
2) Частинні похідні.
3) Логарифмування та потенціювання функцій.
4) Нормальний закон розподілу випадкової величини.
|
|
|
Питання для самостійної роботи:
1) Записати параметри нормального закону розподілу залишків, що підпорядковуються умовам Гауса-Маркова 
2) Зобразити графічно щільність розподілу цієї величини/
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 391; Нарушение авторских прав?; Мы поможем в написании вашей работы!