Линейная оболочка системы векторов

ОПРЕДЕЛЕНИЕ ПОДПРОСТРАНСТВА

ПРИМЕРЫ ЛИНЕЙНЫХ ПРОСТРАНСТВ

1. Множество многочленов P_n (x) степени не выше n.

2. Множество n -членных последовательностей (с почленным сложением и умножением на скаляр).

3. Множество функций C _{[ а, b ]} непрерывных на [ а, b ] и с поточечным сложением и умножением на скаляр.

4. Множество функций, заданных на [ а, b ] и обращающихся в 0 в некоторой фиксированной внутренней точке c: f (c) = 0 и с поточечными операциями сложения и умножения на скаляр.

5. Множество R⁺, если x ⊕ y º x ´ y, a⊙ x º x ^a.

Пусть множество W является подмножеством линейного пространства V (W Ì V) и такое, что

а) " x, y Î W Þ x ⊕ y Î W;

б) " x Î W, "aÎK Þ a ⊙ x Î W.

Операции сложения и умножения здесь те же, что и в пространстве V (они называются индуцированными пространством V).

Такое множество W называется подпространством пространства V.

7°. Подпространство W само является пространством.

◀ Для доказательства достаточно доказать существование нейтрального элемента и противоположного. Равенства 0⊙ x = q и (–1)⊙ х = – х доказывают необходимое. ▶

Подпространство, состоящее только из нейтрального элемента {q}и подпространство, совпадающее с самим пространством V, называются тривиальными подпространствами пространства V.

§ 9. ЛИНЕЙНАЯ КОМБИНАЦИЯ ВЕКТОРОВ.

Пусть векторы e ₁, e ₂, … e_n Î V и a₁, a₂, … a _n ÎK.

Вектор x = a₁ e ₁ + a₂ e ₂ + … + a _ne_n = 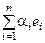называется линейной комбинацией векторов e ₁, e ₂, …, e_n с коэффициентами a₁, a₂, … a _n.

Если все коэффициенты в линейной комбинации равны нулю, то линейная комбинация называется тривиальной.

Множество всевозможных линейных комбинаций векторов называется линейной оболочкой этой системы векторов и обозначается:

ℒ(e ₁, e ₂, …, e_n) = ℒ.

8°. ℒ(e ₁, e ₂, …, e_n) является линейным пространством.

◀ Корректность операций сложения и умножения на скаляр следует из того, что ℒ(e ₁, e ₂, …, e_n) – это множество всевозможных линейных комбинаций. Нейтральный элемент – это тривиальная линейная комбинация. Для элемента х = 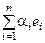противоположным является элемент – x =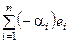. Аксиомы, которым должны удовлетворять операции, также выполнены. Таким образом, ℒ(e ₁, e ₂, …, e_n) является линейным пространством.

Любое линейное пространство содержит в себе в, общем случае, бесконечное множество других линейных пространств (подпространств) – линейных оболочек ▶

В дальнейшем мы постараемся ответить на следующие вопросы:

Когда линейные оболочки разных систем векторов состоят из одних и тех же векторов (т.е. совпадают)?

2) Какое минимальное число векторов определяет одну и ту же линейную оболочку?

3) Является ли исходное пространство линейной оболочкой некоторой системы векторов?

Дата добавления: 2014-01-11