Координаты вектора В ЗАДАННОМ БАЗИСе

ПРИМЕРЫ

1. Набор мономов {1, t, t ²,…, tⁿ } образует базис в пространстве P_n полиномов от t степени не выше n. Линейная независимость набора следует из того, что:

a₁ + a₂ t + … + a _{n +1} tⁿ ≡ 0 Þ a₁ = a₂ = … = a _{n +1} = 0, dim P_n = n +1.

2. Тройки чисел (a₁, a₂, a₃) образуют линейное пространство А ₃ с базисом {(1, 0, 0), (0, 1, 0), (0, 0, 1)}, dim A ₃ = 3. Это пространство называется арифметическим линейным пространством и обозначается А_n .

23°. Пусть V – линейное пространство, dim V = n и 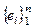– базис в V. Тогда " x Î V существует единственный набор 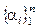, a _i ÎK такой, что x =.

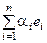◀ Представление x =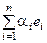следует из полноты .

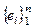Единственность. Пусть 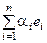x =и x =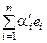. Тогда q = x – x = 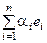– 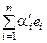= = 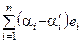и, следовательно, в силу линейной независимости

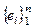, " i a _i – a¢ _i = 0 т.е. a _i = a¢ _i. ▶

Теперь ясно, что если в пространстве V задан базис 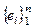, то каждому вектору x Î V можно поставить в соответствие (причем единственным образом) набор чисел a₁, a₂, …, a _n ÎK. Это записывают так: x ↔ (a₁, a₂, …, a _n) или x = (a₁, a₂, …, a _n). Величины a _i называются координатами вектора x в базисе 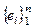. При этом, (что очень важно), если x = (a₁, a₂, …, a _n) и y = (b₁, b₂, …, b _n), то x ⊕ y = (a₁ + b₁, a₂ + b₂, …, a _n + b _n) и g⊙ x = = (ga₁, ga₂, …, ga _n), т.е. операции ⊕ и ⊙ заменены покоординатным сложением и умножением на элемент внешнего поля K.

Другими словами, введение понятия базиса векторного пространства V над полем K и координат векторов в этом базисе абстрактные операции сложения для элементов линейного пространства и умножения их на скаляры из внешнего поля K позволяет свести к операциям покоординатного сложения и умножения на скаляр, т. е. к умножению и сложению в поле K.

Дата добавления: 2014-01-11