Неоднородные системы

Рассматривается неоднородная система линейных уравнений Ах = b с n- неизвест-ными.

12°. (Кронекер-Капелли). Система Ах = b совместна тогда, и только тогда, когда ранг главной матрицы системы совпадает с рангом расширенной матрицы rang A = rang à (à = (A|b)).

◀ 1) Пусть система Ах = b – совместна Þ $ с такой, что Ас = b т.е. c ₁S₁ + c ₂S₂ +…+ c_n S _n = b. Таким образом, последний столбец матрицы Ã является линейной комбинацией столбцов матрицы А Þ rang A = rang Ã.

2). Пусть rang A = Ã. Тогда базисные столбцы общие, т.е. являются столбцами матрицы А Þ столбец b является линейной комбинацией столбцов s _1, s _2, …, s_n Þ $ c ₁, c _2, …, c_n такие, что c ₁ S ₁ + c ₂ S ₂ +…+ c_nS_n = b т.е. Аc = b. Система совместна. ▶

13°. Если неоднородная система линейных уравнений совместна и rang A = rang à = n, то она имеет единственное решение (по теореме Крамера).

Пусть теперь rang A = rang à = r ≤ n.

14°. Разность двух различных решений неоднородной системы линейных уравнений является решением соответствующей однородной системы, т.е. если c ⁽²⁾ и c ⁽¹⁾ два решения неоднородной системы Ах = b, то c ⁽²⁾ – c ⁽¹⁾ решением однородной системы Ах = 0.

◀ А (c ⁽²⁾ – c ⁽¹⁾) = Аc ⁽²⁾ – Аc ⁽¹⁾ = b – b = 0, т.е. c ⁽²⁾ – c ⁽¹⁾ = c ⁽⁰⁾. Здесь через c ⁽⁰⁾ обозначено некоторое решение однородной системы. ▶

15°. Сумма любого решения однородной системы c ⁽⁰⁾ и некоторого решения неоднородной системы c ⁽¹⁾ есть решение неоднородной системы.

◀ А (c ⁽⁰⁾ – c ⁽¹⁾) = Аc ⁽⁰⁾ + Аc ⁽¹⁾ = 0 + b = b. ▶

Предыдущие два утверждения доказывают теорему об общем виде решения неоднородной системы и линейных уравнений.

16°. Общее решение неоднородной системы уравнений есть сумма общего решения однородной системы и некоторого частного решения неоднородной системы. Эту фразу можно записать с помощью легко запоминающейся аббревиатуры:

О. Р. Н. С. = О. Р. О. С. + Ч. Р. Н. С.

Способ решения неоднородных систем линейных уравнений таков:

1). Если rang A = rang à = n, то решение единственно и может быть найдено по Крамеру;

2). Если rang A = rang à = r < n то, записав систему в виде

x ₁ S ₁ + x ₂ S ₂ +…+ x_rS_r = b – x_{r +1} S_{r +1} –…– x_nS_n.

а) положив x_{r +1,} x_{r +2, …,} x_n равными любим фиксированным значениям, получим систему неоднородную (r - уравнений с r -неизвестными) имеющей единственное решение, ибо ее определитель не равен 0. Тем самым будет найдено частное решение неоднородной системы.

b) выбросив вектор b: x ₁ S ₁ + x ₂ S ₂ +…+ x_rS_r = – x_{r +1} S_r+1 –…– x_nS_n и применяя процедуру, описанную в предыдущем параграфе, построим базис в пространстве L решений однородной системы уравнений { e ₁, e₂,..., e_{n – r} }.

с). Тогда x ^{(неодн.)} = x ^{(частн.)} +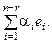

Система векторов { e ₁, e₂,..., e_{n – r} } называется фундаментальной системой решений для системы уравнений Ах = 0.

Если М – множество решений неоднородной системы уравнений, x ^(r)– некоторое частное решение неоднородной системы уравнений, L – пространство решений соответствующей линейной однородной системы, то M = x ^(r)+ L, т.е. М – есть линейное многообразие размерности n – r.

§8. Метод Гаусса РЕШЕНИЯ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ. (метод исключения неизвестных)

Решить систему уравнений: .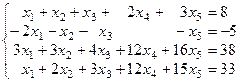

Записав расширенную матрицу системы, преобразуем ее с помощью преобразований не изменяющих ранг матрицы. Цель: в первом столбце все элементы, кроме одного, должны стать равными нулю. Это равносильно тому, что из 2^го, 3^го и 4^го уравнений будет исключена неизвестная х ₁. Для достижения цели первую строку, умноженную на 2, –3 и –1 прибавим, соответственно, к 2^ой, 3^ей и 4^ой строке. Получим:

~.

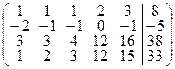Примечание: здесь и в дальнейшем знак ~, стоящий между двумя матрицами означает, что справа и слева от этого знака стоят матрицы одинакового ранга и, следовательно, системы линейных уравнений с такими матрицами имеют одинаковые решения.

Далее вторую строку, умноженную на –1 прибавим к 4^ой строке, тем самым исключив х ₂ из третьего и четвертого уравнений и, наконец исключим х ₃ из 4^го уравнения, прибавив третью строку, умноженную на –1 к четвертой:

~ ~ .

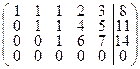Имеем rang A = rang à = 3. Система совместна. n – r = 5 –3 = 2, dim L = dim M = 2. Так как, размерность пространства решений однородной системы равна 2, то в системе имеется две свободных неизвестных. Выберем в качестве свободных переменных х ₃, х ₄. Отделим в матрице свободные неизвестные вертикальной пунктирной линией: .

Положив х ₄ = 1, х ₅ = 1, получим х ₁ = х ₂ = х ₃ = 1. Т.е. частное решение неоднородной системы (1, 1, 1, 1, 1).

Далее рассмотрим однородную систему уравнений с матрицей 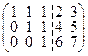. Тогда

.

Положив х ₄ = 1, х ₅ = 0 Þ е ₁(2, 2, –6, 1, 0). Положив х ₄ = 0, х₅ = 1 Þ е ₂(2, 2, –7, 0, 1), (е ₁, е ₂ – ба­зис пространства решений). Отсюда х = (1,1,1,1,1) + a(2,2,–6,1,0) + b(2,2,–7,0,1), где a, b – любые.

Если положить х ₄ = х ₅ = 0, то получим х ₃ = 14, х ₂ = –3, х ₁ = –3, т.е. (–3, –3, 14, 0, 0) еще одно частное решение данной системы. Следовательно, общее решение исходной системы можно записать и в таком виде: х = (–3, –3, 14, 0, 0) + a(2, 2, –6, 1, 0) + b(2, 2, –7, 0, 1), где a, b – любые.

Нужно обратить внимание и на то, что разность двух частных решений неоднородной системы (–3, –3, 14, 0, 0) – (1, 1, 1, 1, 1) есть решение соответствующей однородной системы уравнений.

§9. «Альтернатива Фредгольма»

Для квадратной системы 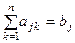(j =1, 2, …, п):

а) или система имеет решение, притом единственное при любых b_j, если соответствую­щая однородная система имеет только тривиальное решение (det A ≠ 0),

б) или соответствующая однородная система имеет ненулевые решения (det A = 0) и, следовательно, есть такие b_j, при которых система не имеет решений.

РАЗДЕЛ 6. Билинейные и квадратичные формы

Дата добавления: 2014-01-11