Знакопеременные ряды. Абсолютная и условная сходимость числовых рядов

Числовой ряд 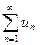, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным.

Теорема (общий достаточный признак сходимости знакопеременных рядов).

Пусть дан знакопеременный ряд.

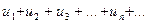(4.3.5)

Если сходится ряд

, (4.3.6)

составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд.

Обратное утверждение несправедливо, если сходится ряд (4.3.5), то это не означает, что будет сходится ряд (4.3.6).

Замечание: из расходимости ряда , расходимость ряда 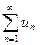вообще не следует.

Но если к ряду применив признак Даламбера (или Коши), получаем

- то в этом случае оба ряда (4.3.5) и (4.3.6) расходятся.

Определение. Знакопеременный ряд называется абсолютно сходящимся, если ряд, составленный из модулей его членов, сходится.

Опр. Знакопеременный ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.

Пример: исследуем сходимость ряда

Ряд знакочередующийся, для которого выполняются условия признака Лейбница.

1) члены ряда убывают по абсолютной величине ;

2) .

Поэтому ряд сходится по признаку Лейбница.

Ряд, составленный из модулей

- является гармоническим, который, как известно, расходится. Т.е. исходный ряд является условно сходящимся.

Основные свойства абсолютно сходящихся рядов:

1) Если ряд абсолютно сходится и имеет сумму S, то ряд, полученный из него перестановкой членов, также сходится, и имеет ту же сумму S, что и исходный ряд.

2) Абсолютно сходящиеся ряды с суммами и 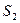можно почленно складывать (вычитать). В результате получается абсолютно сходящийся ряд, сумма которого равна (или соответственно )

3) Произведение двух абсолютно сходящихся рядов с суммами и 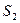есть абсолютно сходящийся ряд, сумма которого равна 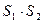(ряды умножаются по правилу умножения многочленов).

4) В случае условно сходящихся рядов эти свойства, вообще говоря, не имеют смысла.

Пример: ряд условно сходится.

Пусть его сумма равна S. Перепишем его члены так, что после одного положительного члена будут идти два отрицательных.

Получим ряд

Сумма уменьшилась вдвое.

Более того, путем перестановки членов условно сходящегося ряда можно получить сходящийся ряд с заранее заданной суммой или расходящийся ряд.

Дата добавления: 2014-01-11