Сходимость степенных рядов

Теорема (Абеля). Рассмотрим степенной ряд

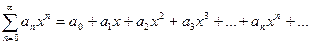(4.4.4)

Если степенной ряд сходится при 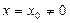, то он абсолютно сходится при всех значениях х, удовлетворяющих неравенству 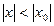. Если степенной рядрасходится в точке x₀, то он расходится при всех значениях x, для которых .

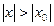Из теоремы Абеля следует:

1) если 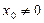- есть точка сходимости ряда, то интервал - сплошь состоит из точек сходимости данного ряда.

2) Для каждого степенного ряда существует определенное число 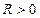такое, что ряд (4) абсолютно сходится при всех значениях х, когда 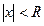и ряд (4.4.4) расходится для тех значений х, когда 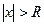. Число R называют радиусом сходимости степенного ряда.

3) область сходимости степенного ряда есть промежуток 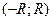- его называют интервал сходимости.

Интервал сходимости симметричен относительно начала координат. На концах интервала, т.е. при x=R и x=-R сходимость проверяется в каждом случае отдельно.

Когда ряд сходится лишь в одной точке 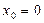, то радиус сходимости R=0 и ряд является расходящимся, Если же ряд сходится при всех значениях (т.е. во всех точках числовой оси), то считаем что .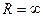

Для отыскания радиуса сходимости (числа R) поступают следующим образом:

Составим ряд из модулей членов данного степенного ряда

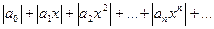(4.4.5)

И применим к нему признак Даламбера:

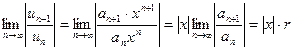, где .

Допустим, что этот предел существует, тогда по признаку Даламбера ряд (4.4.5) сходится, если и расходится, если 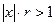, т.е. ряд сходится, ес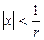ли или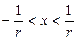

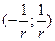- интервал сходимости.

Таким образом, для ряда (4.4.4) радиус абсолютной сходимости можно найти по формуле

(4.4.6)

Аналогично, воспользовавшись радикальным признаком Коши можно установить, что

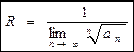(4.4.7)

Замечание: 1) интервал сходимости степенного ряда (4.4.3) находят из неравенства: , интервал имеет вид

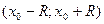
2) если степенной ряд содержит не все степени х, т.е. задан неполный степенной ряд, то интервал сходимости находят непосредственно, применяя признак Даламбера или Коши. Формулы (4.4.6) и (4.4.7) не используют.

Пример1. Найти область сходимости ряда .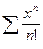

Используем признак Даламбера:

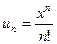
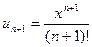
для любого х, т.е. область сходимости (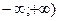

Используя формулу (4.4.6)

.

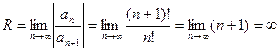
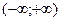Пример 2. Найти область сходимости ряда

Заданный ряд неполный. Используем признак Даламбера:

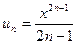
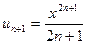
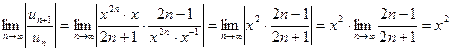
Ряд сходится, если . Интервал сходимости .

Исследуем сходимость на концах интервала.

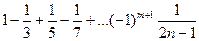, получаем ряд , ряд сходится по признаку Лейбница.

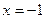, получаем ряд , ряд сходится по признаку Лейбница, т.е. интервал сходимости отрезок .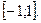

Дата добавления: 2014-01-11