Ряды фурье

Некоторые приложения степенных рядов

1) Ряды Тейлора используются для приближенного вычисления значений функции.

Найти 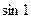с точностью 0,001

Разложение функции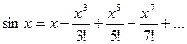

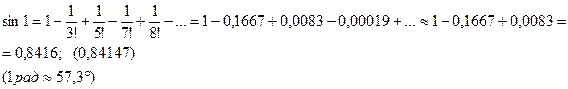
2) Бесконечные ряды применяются также для приближенного вычисления неопределенных и определенных интегралов в случаях, когда первообразная не выражается в конечном виде через элементарные функции, либо нахождение первообразной сложно.

Пусть требуется вычислить 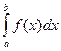с точностью до 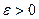. Если подынтегральную функцию 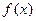можно разложить в ряд по степеням х и интервал сходимости 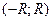включает в себя отрезок 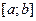, то для вычисления заданного интеграла нужно воспользоваться свойством почленного интегрирования этого ряда.

Пример: 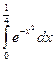с точностью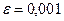

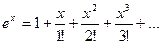вместо 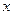подставим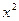

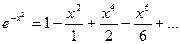
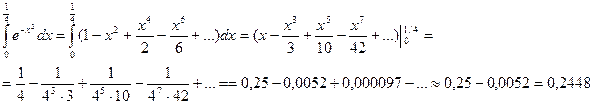
3) Приближенное решение дифференциальных уравнений.

Если решение дифференциального уравнения не выражается через элементарные функции или способ его решения слишком сложен, то для приближенного решения уравнения можно воспользоваться рядом Тейлора.

Пусть требуется найти решение дифференциального уравнения второго порядка

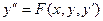, (4.7.1)

удовлетворяющее начальным условиям

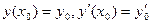. (4.7.2)

Допустим, что решение существует и представлено в виде ряда Тейлора

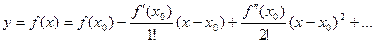
Нам нужно найти коэффициенты ряда

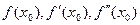и т.д., т.е. значения производных от частного решения при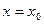

Это можно сделать при помощи заданного уравнения (4.7.1) и начальных условий (4.7.2).

Из условий (4.7.2) следует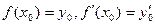

Из уравнения (4.7.1) получаем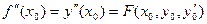

Дифференцируя уравнение (4.7.1) по х (обе части) находим третью производную

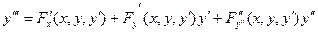(4.7.3)

Подставляем значение 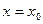, найдем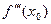

Дифференцируя соотношение (4.7.3) найдем 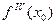и т.д.

Частичная сумма ряда будет приблизительным решением дифференциального уравнения.

Способ последовательного дифференцирования применим для решения дифференциальных уравнений любого порядка.

Пример: Найти четыре первых члена (отличных от нуля) разложения в ряд решения уравнения 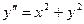, удовлетворяющего начальным условиям .

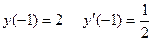Решение уравнения будем искать в виде:

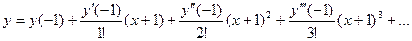
Имеем: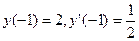

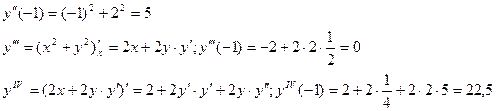
Искомое решение.

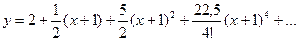
Пример2. Найти частное решение уравнения .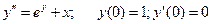

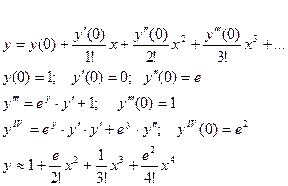
Вопросы для самоконтроля.

1. Определение числового ряда. Как задается числовой ряд?

2. Определение сходимости и расходимости числового ряда.

3. Необходимый признак сходимости числового ряда.

4. Достаточные признаки сходимости знакопостоянных рядов.

5. Гармонический и обобщенный гармонический ряд.

6. Знакочередующиеся ряды. Признак Лейбница.

7. Знакопеременные ряды. Абсолютная и условная сходимость числовых рядов. Общий достаточный признак сходимости знакопеременных рядов.

8. Функциональные ряды. Степенной ряд. Нахождение интервала сходимости степенного ряда. Свойства степенных рядов.

9. Разложение произвольной функции в ряд Тейлора.

10. Разложение элементарных функций в ряд Маклорена.

11. Чем отличается ряд ямаклорена от ряда Тейлора?

12. Приложения степенных рядов.

Литература: [5] стр. 254-275,стр. 299-301, [6] стр. 438-475, [7] стр. 351-397.

Примеры: [2] стр. 66-95, [3] стр. 128-189.

Дата добавления: 2014-01-11