Тригонометрический ряд Фурье

Покажем, что практически любую периодическую функцию можно представить в виде ряда, членами которого являются простые гармоники, с помощью, так называемого, тригонометрического ряда.

Определение. Тригонометрическим рядом называется функциональный ряд вида

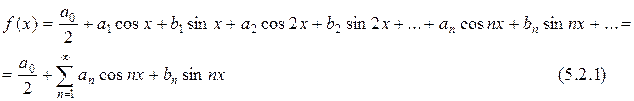
где действительные числа а ₀, а_n, b_n называются коэффициентамиряда.

Свободный член ряда записан в виде 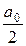для единообразия получающихся в дальнейшем формул.

Нужно решить два вопроса:

1) При каких условиях функция f(x) с периодом 2π может быть разложена в ряд (5.2.1)?

2) Как вычислить коэффициенты а ₀,… а_n, b_n?

Начнем с решения второго вопроса. Пусть функция f(x) непрерывна на отрезкеи имеет период Т=2π. Приведем формулы, которые понадобятся нам в дальнейшем.

I.

При любом целом 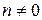, так как функция 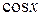четная.

II.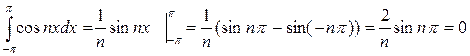

При любом целом .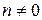

III.

(m и n целые числа)

IV.

V.

При 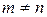(m и n целые числа) каждый из интегралов (III, IV, V) преобразуется в сумму интегралов (I) или (II). Если же , то в формуле (IV) получаем:

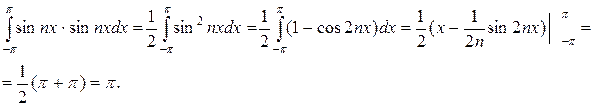
Анологично доказывается равенство (V).

Предположим теперь, что функция 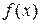оказалась такой, что для неё нашлось разложение в сходящийся ряд Фурье, то есть

(5.2.2)

(Следует обратить внимание, что суммирование идёт по индексу n).

Если ряд сходится, то его сумму обозначим S(x).

Почленное интегрирование (законное в силу предположения о сходимости ряда) в пределах от до даёт

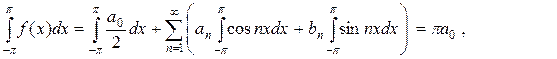
так как все слагаемые кроме первого равны нулю (соотношения I, II). Отсюда находим

(5.2.3)

Умножая (5.2.2) на 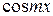(m =1,2,…) и почленно интегрируя в пределах от до , найдем коэффициент a_n.

В правой части равенства все слагаемые равны нулю, кроме одного m=n (соотношения IV, V), Отсюда получаем

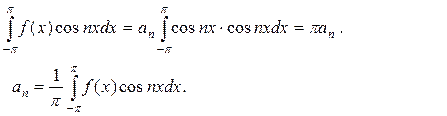(5.2.4)

Умножая (5.2.2) на (m =1,2,…) и почленно интегрируя в пределах от до ,аналогичным образом находим коэффициент b_n

(5.2.5)

Значения 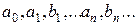- определяемые по формулам (5.2.3), (5.2.4), (5.2.5) называются коэффициентами Фурье, а тригонометрический ряд (5.2.2) – ряд Фурье для данной функции f(x).

Итак, получили разложение функции f(x) в ряд Фурье

Вернемся к первому вопросу и выясним какими свойствами должна обладать функция f(x), чтобы построенный ряд Фурье был сходящимся, и сумма ряда равнялась бы именно f(x).

Определение. Функция f(x) называется кусочно-непрерывной, если она непрерывна или имеет конечное число точек разрыва I рода.

Определение. Функция f(x), заданная на отрезке называется кусочно-монотонной, если отрезок можно разбить точками на конечное число промежутков, в каждом из которых функция изменяется монотонно (возрастая или убывая).

Будем рассматривать функции f(x), имеющие период Т=2π. Такие функции называются 2π - периодическими.

Сформулируем теорему, представляющую достаточное условие разложимости функции в ряд Фурье.

Теорема Дирихле (примем без доказательства). Если 2π -периодическая функция f(x) на отрезке является кусочно-непрерывной и кусочно-монотонной, то соответствующий функции ряд Фурье сходится на этом отрезке и при этом:

1. В точках непрерывности функции сумма ряда совпадает с самой функцией S(x)=f(x);

2. В каждой точке х₀ разрыва функции f(x) сумма ряда равна ,

т.е. среднему арифметическому пределов функции слева и справа от точки х₀;

3. В точках (на концах отрезка) сумма ряда Фурье равна ,

т.е. среднему арифметическому предельных значений функции на концах отрезка, при стремлении аргумента к этим точкам изнутри промежутка.

Замечание: если функция f(x) с периодом 2π непрерывна и дифференцируема во всем промежутке и значения ее на концах промежутка равны, т.е.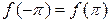, то ввиду периодичности эта функция непрерывна на всей числовой оси и при любом х сумма ее ряда Фурье совпадает с f(x).

Таким образом, если интегрируемая на отрезке функция f(x) удовлетворяет условиям теоремы Дирихле, то на отрезке имеет место равенство (разложение в ряд Фурье):

Коэффициенты вычисляются по формулам (5.2.3) - (5.2.5).

Условиям Дирихле удовлетворяет большинство функций, которые встречаются в математике и ее приложениях.

Ряды Фурье, как и степенные ряды, служат для приближенного вычисления значений функций. Если разложение функции f(x) в тригонометрический ряд имеет место, то всегда можно пользоваться приближенным равенством 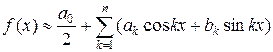, заменяя данную функцию суммой нескольких гармоник, т.е. частичной суммой (2 n +1) члена ряда Фурье.

Тригонометрические ряды широко используют в электротехнике, с их помощью решают многие задачи математической физики.

Пример.

Разложить в ряд Фурье функцию 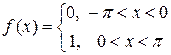с периодом 2π, заданную на интервале (-π;π).

Решение. Найдем коэффициенты ряда Фурье:

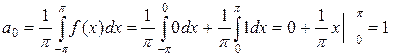
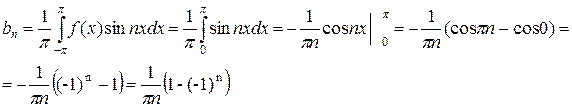
Получили разложение функции в ряд Фурье

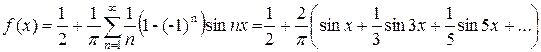
В точках непрерывности сумма ряда Фурье равна значению функции f(x)=S(x), в точке х=0 S(x)=1/2, в точках х=π,2π,… S(x)=1/2.

Дата добавления: 2014-01-11