Висновок

Вступ

План

1. Вступ

2. Числові послідовності

2.1. Поняття послідовності

2.2. Загальний член послідовності

2.3. Способи задання послідовності

3. Арифметична прогресія

3.1. Поняття арифметичної прогресії

3.2. Сума перших п членів арифметичної прогресії

4. Геометрична прогресія

4.1. Поняття геометричної прогресії

4.2. Сума перших п членів геометричної прогресії

5. Розв’язування вправ і задач на прогресії

6. Висновок

7. Список використаної літератури

Російський математик С.Л. Соболєв сказав: «Є одна наука, без якої неможлива ніяка інша. Це математика. Її поняття, уявлення та символи слугують тією мовою, якою говорять, пишуть і думають інші науки. Вона пояснює закономірність складних явищ, приводить їх до простих, елементарних явищ природи. Вона прогнозує, обчислює далеко вперед з великою точністю хід речей».

Одна з найцікавіших тем математики – прогресії. У перекладі з латинської слово прогресія означає рух уперед. Прогресії відомі здавна, а тому не можна сказати, хто їх відкрив. Адже і натуральний ряд 1, 2, 3, 4, … - це арифметична прогресія, в якої 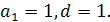Під час розкопок у Єгипті було знайдено папірус, що датується 2000 р. до н.е., але і його було переписано з іншого, ще давнішого, віднесеного до третього тисячоліття до н.е. Учені розшифрували текст папірусу і прочитали кілька задач. Зміст деяких з них дає можливість віднести їх до задач на прогресії.

Про те, як давно була відома геометрична прогресія, свідчить і легенда про історію винайдення шахів.

Винахідник шахів попросив у нагороду за свій винахід стільки пшеничних зерен, скільки їх вийде, якщо на першу клітинку шахівниці покласти одну зернину, на другу – у два рази більше, тобто дві зернини і т.д. Ми маємо справу з геометричною прогресією, в якої 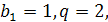а кількість членів 64.

Задачі на прогресії зустрічаються в одній з найдавніших пам’яток права – «Руській правді», укладеній ще за київського князя Ярослава Мудрого (ХІст.). Там є стаття, присвячена обчисленню приплоду від 22 овець за 12 років за умови, що кожна вівця щорічно приносить 1 вівцю і 2 барани.

Значна кількість задач на прогресії є в «Арифметиці» Л.Магницького (1703), що була основним математичним підручником у Росії протягом майже півстоліття.

Прогресії є відображенням світу, що нас оточує. Вони застосовуються в таких науках, як: фізика – під час вивчення тіл, що вільно падають чи рухаються рівноприскорено; економіка та банківська справа – під час виплати відсотків та надання кредитів; у техніці – під час виготовлення обладнання.

Сучасна шкільна програма пропонує цей розділ розглядати у 9-му класі. Передбачається спочатку дати загальне поняття послідовності, а вже потім детальніше розглянути арифметичну і геометричну прогресії.

2. Числові послідовності

2.1. Поняття послідовності

Як вводити поняття послідовності?

Починати пояснювати краще не з означення, а з конкретних прикладів:

- Напишемо натуральні числа в порядку їх зростання: 1. 2, 3, 4, 5, 6, 7…

Це – послідовність натуральних чисел. А ось ще кілька прикладів:

§ 2, 4, 6, 8, 10, 12, … - послідовність парних чисел;

§ 1, 3, 5, 7, 9, 11,... - послідовність непарних чисел;

§ 2, 3, 5, 7, 11, 13,... - послідовність простих чисел;

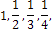§ … - послідовність чисел, обернених до натуральних;

§ 1; 1,4; 1,41;... - послідовність наближених значень .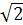

Числа, що належать послідовності, називаються її членами. Наприклад, у послідовності парних чисел перший член 2, другий член - число 4, десятий член - число 20 і т. д. Членами числової послідовності можуть бути будь-які числа: цілі й дробові, додатні й від’ємні, раціональні й ірраціональні.

Чим відрізняється послідовність від множини? По-перше, тим, що для послідовності істотне значення має порядок її членів, а для множини він не має ніякого значення. Наприклад, множини

{1, 2, 3, 4, 5, 6, 7, 8, 9} і {3, 7, 1, 9, 5, 4, 2, 8, 6}

однакові, а послідовності

1, 2, 3, 4, 5, 6, 7, 8, 9 і 3, 7, 1, 9, 5, 4, 2, 8, 6

різні. По-друге, вважають, що всі елементи множини різні, а послідовність може мати й однакові члени.

Приблизно так можна ввести поняття числової послідовності. Потім можна сказати, що послідовності бувають нескінченні й скінченні, останні ще називають кортежами. Бажано також дати поняття зростаючої і спадної послідовності. Іноді зростаючою називають таку числову послідовність, в якої кожний член, починаючи з певного місця, більший від попереднього [7, 6]. Зокрема, до зростаючих відносять і таку послідовність: 37, 26, 17. 10, 5, 2, 1, 2, 5,..., загальний член якої 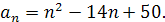. Проте я не вважаю доцільним так розширювати це поняття. Зростаючою краще називати тільки таку числову послідовність, кожний член якої, крім першого, більший від попереднього. Якщо ж кожний член числової послідовності, крім першого, не менший від попереднього, то таку послідовність бажано називати неспадною. Зростаюча послідовність є окремим видом неспадної. Аналогічно можна означити спадну і незростаючу послідовності.

2.2. Загальний член послідовності

Поняття загального члена числової послідовності обов’язково треба ввести. Але у 9-му класі можна не давати строге означення загального члена числової послідовності. Пояснити це краще на конкретних прикладах.

- Розглянемо ще раз послідовність парних чисел: 2, 4, 6, 8, 10, 12,.... Її перший член дорівнює 2, другий - 4, третій - 6 і т. д. Пишуть: 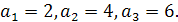А чому дорівнює п -й член цієї послідовності? Оскільки кожний член послідовності парних чисел вдвоє більший від свого порядкового номера, то п -й член її дорівнює 2 п. Пишуть: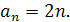

п -й член послідовності називають її загальним членом.

Якщо відомий загальний член послідовності, то можна написати скільки завгодно її членів. Для цього досить замість букви, що входить до загального члена, підставляти послідовно натуральні числа - номери членів. Нехай, наприклад, треба знайти кілька перших членів послідовності з загальним членом 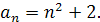Надаючи букві п значень 1, 2, 3, 4, 5,..., дістанемо:

3, 6, 11, 18, 27,....

Значно важче розв’язувати обернену задачу: за даними першими членами послідовності написати її загальний член. Тільки в простіших випадках вдається порівняно швидко розв’язати цю задачу. А взагалі знаходження загального члена послідовності пов’язане із значними труднощами. Є й такі послідовності, загальні члени яких ще нікому не відомі. Такою, наприклад, є послідовність простих чисел

2, 3, 5, 7, 11, 13, 17, 19, 23. 29,....

Коли відомо лише кілька перших членів послідовності, то її загальний член взагалі не можна визначити однозначно. Наприклад, коли написано:

1, 3, 5, 7, 9, …,

то це може бути послідовність із загальним членом 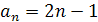або 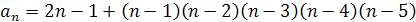і т.п.

Є безліч різних числових послідовностей, п’ять перших членів яких 1, 3, 5, 7, 9. Тому вчитель повинен знати, що щоб задати послідовність, не досить вказати кілька її перших членів.

Але як усе-таки визначити загальний член хоч однієї з послідовностей, що мають задані перші члени? Учням ніяких правил для цього можна не давати, але й важких вправ на визначення загального члена послідовності також їм не треба пропонувати. Складніші вправи треба розглядати як вправи для кмітливих.

Але вчителеві треба знати й загальніший спосіб розв’язування таких вправ. Нехай, наприклад, вимагається визначити загальний член послідовності

6, 9, 14. 21, 30, 41,....

Щоб розв’язати задачу, учень змушений добирати різні формули і випробовувати їх. Не виключено, що йому так і не вдасться знайти потрібну формулу. Вчитель може діяти цілеспрямованіше. Тут треба записати послідовність різниць суміжних членів даної послідовності, а потім другу послідовність різниць і т.д., поки не дістанемо послідовність різниць з однаковими членами. Пишемо:

6 9 14 21 30 41

3 5 7 9 11

2 2 2 2

Як бачимо, всі члени другої послідовності різниць однакові. Це свідчить про те, що загальний член послідовності (найпростіший) є многочленом другого степеня [7, 10].

Записуємо цей загальний член з невизначеними коефіцієнтами:

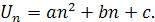
Залишається визначити коефіцієнти а, b, c. Це можна зробити так. Оскільки, підставляючи в цю формулу замість п числа 1, 2, 3, ми повинні дістати відповідно значення 6, 9, 14 (перші члени даної послідовності), то маємо систему

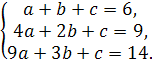
Розв’язавши її, дістанемо 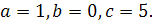Отже, найпростіший загальний член даної послідовності

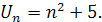
2.3. Способи задання послідовності

Тільки після того, як учні добре зрозуміють, що таке послідовність, її загальний член, можна розповісти їм про різні способи задання числової послідовності. При цьому бажано підвести їх до функціонального трактування цього поняття.

- Згадаймо означення функції. Функцією називається відповідність, при якій кожному елементові однієї множини відповідає один елемент другої множини.

А в числовій послідовності кожний член поставлений у відповідність його номеру - натуральному числу. Так, коли перший, другий, третій і т.д. члени послідовності дорівнюють 6, 9, 14, 21, 30, 41,..., то це можна розглядати як відповідність:

1 2 3 4 5 6....

↓ ↓ ↓ ↓ ↓ ↓

6 9 14 21 30 41....

Отже, нескінченну числову послідовність можна розглядати як функцію, задану на множині всіх натуральних чисел. Відомо, що функцію можна задати аналітично, таблично, графічно. Аналогічними способами можна задавати і послідовності.

Наприклад, ми можемо сказати: «послідовність, загальний член якої 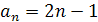». Цим самим ми задали послідовність. Такий спосіб задання послідовності за допомогою формули загального члена можна назвати аналітичним способом. Цю послідовність можна задати і з допомогою такої таблиці:

n									…
an									…

Правда, без верхнього рядка (значень аргументу п) тут можна обійтись, бо ці значення збігаються з порядковими номерами членів послідовності. Можна записати це простіше:

1, 3, 5, 7, 9, 11, 13, 15,...,

маючи на увазі, що перший член цієї послідовності 1 відповідає аргументу 1, п’ятий член 9 відповідає аргументу 5 і т. д.

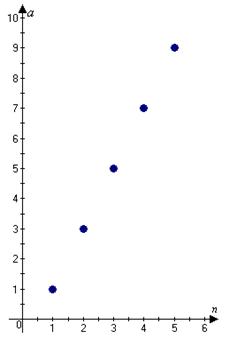Можна цю саму послідовність задати і графічно, відкладаючи на координатній площині точки (1; 1), (2; 3), (3; 5), (4; 7) і т. д. (Рис. 1).

Деякі вчителі, будуючи графік послідовності, спочатку наносять на координатну площину точки графіка, а потім сполучають їх послідовно відрізками або проводять через них плавну криву лінію. Цього робити не слід. Навпаки, треба підкреслити, що графік послідовності складається з окремих ізольованих одна від одної точок.

Рис. 1

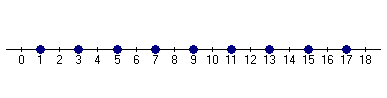Бажано показати учням, як можна зображати числову послідовність на числовій осі. Наприклад, на рис. 2 дано геометричне зображення послідовності непарних чисел, а на рис. 3 - послідовності чисел, обернених натуральним.

Рис. 2

Рис. 3

Нова програма пропонує ознайомити учнів також із заданням числових послідовностей за допомогою рекурентних формул, що дають можливість визначати будь-який член цієї послідовності через попередні її члени. Наприклад, рекурентна формула 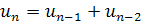описує послідовність, в якої кожний член, починаючи з третього, дорівнює сумі двох попередніх. Таких послідовностей є безліч, наприклад:

1, 3, 4, 7, 11, 18, 29,....

1, -1, 0, -1, -1, -2, -3,....

Якщо ми, крім формули 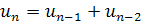, вкажемо і два перших члени послідовності, то цим самим буде визначено однозначно послідовність. Так, ця формула разом з додатковою умовою 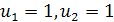визначає відому послідовність Фібоначчі:

1, 1, 2, 3, 5, 8, 13, 21,....

Рекурентна формула 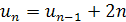при 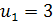визначає послідовність

3, 7, 13, 21, 31, 43, …, , ….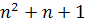

Рекурентна формула 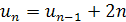при 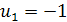визначає послідовність

-1, 3, 9, 17, 27, …, , ….

3. Арифметична прогресія

3.1. Поняття арифметичної прогресії

Часто пояснюють, що «арифметичною прогресією називається така числова послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додають одне й те саме число». Означення арифметичної прогресії можна дати й так: арифметичною прогресією називається кожна числова послідовність, задана рекурентною формулою 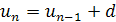, де d - стале число. Це число називається різницею прогресії.

Можна зробити наголос і на функціональному трактуванні арифметичної прогресії, тоді краще починати пояснення так:

- Ми знаємо з означення числової послідовності, що це функція, задана на множині натуральних чисел. Але функції бувають лінійні, квадратні та інші. Зараз ми детально розглянемо лінійну функцію, задану на множині натуральних чисел.

Відомо, що лінійною називають функцію, задану рівністю 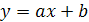. Якщо ж у цій формулі аргумент х пробігатиме тільки множину натуральних чисел, значення функції становитимуть арифметичну прогресію. Правда, аргумент функції, заданої на множині натуральних чисел, частіше позначають буквою п, а не х. Тому можна сказати і так: послідовність, задану формулою 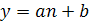, де а і b - дані числа, а п - змінна, яка може набувати тільки натуральних значень, називається арифметичною прогресією. Наприклад, формула 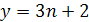визначає таку арифметичну прогресію:

5, 8, 11, 14, 17,....

Після цього можна ввести поняття різниці арифметичної прогресії, записати арифметичну прогресію у вигляді

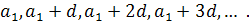
Звідки індуктивно дістати формулу її загального члена:

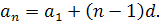
Але можна вивести її також з рекурентної формули 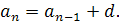Для цього треба записати формулу при п = 2, 3,..., п і додати 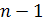рівностей:

+.............

_____________________

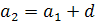
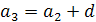
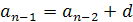
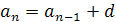
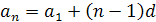
Бажано дати учням і символічне позначення арифметичної прогресії ÷. Нагадуємо, що кілька перших членів послідовності не визначають її однозначно. Тому, коли написано, наприклад,

3, 11, 19, 27, 35. 43,....

це ще не означає, що написано арифметичну прогресію. Якщо ж перед цією послідовністю поставити знак ÷, то дістанемо цілком визначену послідовність.

3.2. Сума п членів арифметичної прогресії

Формулу

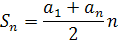
в усіх посібниках виводять однаково. Спочатку показують, що сума двох членів скінченної арифметичної прогресії, рівновіддалених від початку і кінця, дорівнює сумі першого і останнього членів. Але перед цим краще розглянути конкретний приклад.

- Нехай треба знайти суму членів такої скінченної арифметичної прогресії:

3, 5, 7, 9, 11, 13, 15, 17.

Це можна зробити і послідовним додаванням. Проте краще згрупувати ці числа: перше з останнім, друге з передостаннім і т. д.

S=(3+17)+(5+15)+(7+13)+(9+11)=20·4=80.

У цій арифметичній прогресії суми членів, рівновіддалених від початку і кінця, рівні між собою. Це і дало можливість спростити обчислення. Таку властивість має кожна арифметична прогресія.

Після цього можна навести і загальні міркування.

Розглянемо довільну арифметичну прогресію

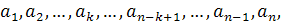
в якої a_k k-й член від початку (k - довільне натуральне число, менше від п). Тоді k-й член від кінця буде a_{n-k +1} .

Покажемо, що

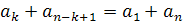
Справді,

, .

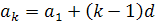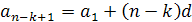Отже,

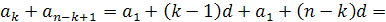
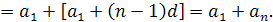
Теорему доведено. Це доведення учням дається нелегко, тому в слабких класах можна замість нього провести міркування за індукцією.

- Запишемо п перших членів довільної арифметичної прогресії:

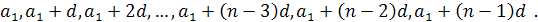
Бачимо, що

..................................................

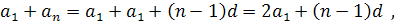
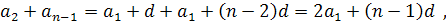
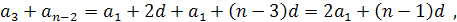
Такою самою буде і сума 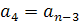, бо коли перший доданок збільшити на d, а другий зменшити на d, сума не зміниться.

Це міркування нестроге, але, як показує досвід, воно набагато зрозуміліше учням, ніж строгі доведення.

Потім пояснення можна продовжити так:

+

_____________________________________________________________________

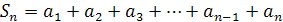
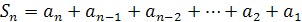
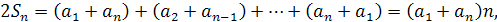
звідки

.

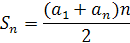4. Геометрична прогресія

4.1. Поняття геометричної прогресії

Ввести поняття геометричної прогресії в 9-му класі можна так:

- Досі ми розглядали арифметичну прогресію, тобто числову послідовність, в якої різниця між кожним членом, крім першого, і попереднім однакова. А тепер розглянемо таку числову послідовність, в якої частка від ділення кожного члена, крім першого, на попередній однакова. Такі послі­довності називають геометричними прогресіями.

Після цього можна навести приклади геометричних прогресій:

3, 6, 12, 24, 48, 96, … ;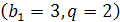

1, -3, 9, -27, 81, -243, … ;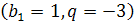

7, 7, 7, 7, 7, 7, 7, 7, … ,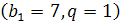

ввести поняття знаменника прогресії і т. д. Означення можна дати аналогічне означенню арифметичної прогресії: геометричною прогресією називається числова послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, помноженому на одне й те саме число. Це стале для даної послідовності число q називають знаменником геометричної прогресії. Або таке означення: геометричною прогресією називається числова послідовність, яку можна задати рекурентною формулою 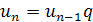, де q - стале число.

Треба добитися, щоб учні вільно записували будь-яку геометричну прогресію у вигляді

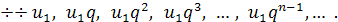
Загальний член цієї прогресії можна дістати, міркуючи за індукцією або розписавши рекурентну формулу 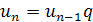для п = 2, 3,..., п і помноживши знайдені формули:

×............

____________

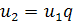
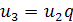
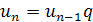
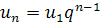
Варто підкреслити, що геометричну прогресію, як і кожну числову послідовність, можна задати не лише рекурентною формулою і загальним членом, а й таблично і графічно.

Далі можна пояснити учням про зростаючі та спадні геометричні прогресії:

- Геометрична прогресія із знаменником 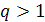- зростаюча, із знаменником 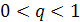- спадна, якщо 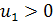, і навпаки, якщо .

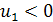Іноді розглядають і прогресії із знаменником , їх називають стаціонарними послідовностями.

Знаменник геометричної прогресії не може дорівнювати нулю. Наприклад, послідовність 3, 0, 0, 0,... не є геометричною прогресією.

4.2. Сума перших п членів геометричної прогресії

Формулу суми перших п членів геометричної прогресії

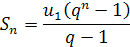
майже в усіх посібниках доведено однаково.

- Запишемо п перших членів довільної геометричної прогресії:

.

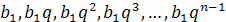Нехай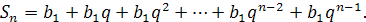

Помножимо обидві частини цієї рівності на q:

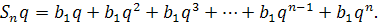
Віднімемо почленно від цієї рівності попередню. При цьому їх однакові доданки 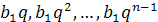взаємно знищаться. В результаті матимемо:

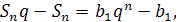
або

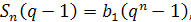
звідки

.

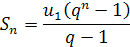Зауважимо, що при цією формулою користуватися не можна (ділити на 0 не можна). У цьому випадку кожен член геометричної прогресії дорівнює 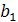, тому .

У зв’язку з формулою суми перших п членів геометричної прогресії бажано було б розглянути і тотожність

яка є узагальненням різниці квадратів і різниці кубів і яку досить часто використовують у різних розділах математики.

5. Розв’язування вправ і задач на прогресії

Під час вивчення прогресій учням бажано пропонувати розв’язувати багато задач і вправ. Бажано підбирати до уроку завдання різної складності залежно від рівня підготовленості учнів. Для прикладу розв’яжемо наступні задачі.

1. В якої арифметичної прогресії десятий і двадцятий члени дорівнюють відповідно 20 і 50?

Розв’язання. Позначимо перший член і різницю шуканої арифметичної прогресії буквами 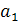і d. Тоді

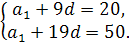
Розв’яжемо систему цих двох рівнянь. Віднявши від другого рівняння перше, дістанемо 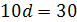, звідки d = 3.

Тепер підставимо це значення в перше рівняння: 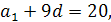звідки .

Отже, , d = 3.

Відповідь. Умову задачі задовольняє

÷ -7, -4, -1, 2, 5, 8, 11, 14, ….

2. Сума трьох чисел, які утворюють геометричну прогресію, дорівнює 21. Якщо до першого з них додати 5, до другого 4, а третє залишити без змін, то утворені числа становитимуть арифметичну прогресію. Знайти ці числа.

Розв’язання. Нехай дано такі числа: и, иq і иq². Якщо до першого додати 5, до другого 4, а трете залишити без змін, то дістанемо:

и + 5, иq + 4, uq ².

Ці числа становлять арифметичну прогресію. Це означає, що різниці між третім і другим, а також між другим і першим рівні:

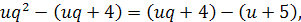
звідки дістаємо таке рівняння:

.

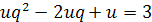Друге рівняння дістанемо, записавши, що сума даних чисел дорівнює 21, тобто

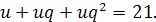
Як бачимо, задача зводиться до розв’язування системи

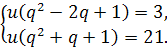
Поділивши друге рівняння на перше, дістанемо

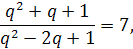
звідки

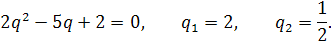
Тоді 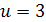або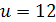

Відповідь. Шукані числа такі: 3, 6 і 12, або 12, 6 і 3.

Розділ «Числові послідовності» - один із найцікавіших і важливих розділів математики. Основна мета вивчення матеріалу даного розділу – ознайомити учнів з поняттями послідовності, арифметичної і геометричної прогресії, формулами п -го члена і суми п членів прогресії.

Протягом вивчення важливо показати практичну спрямованість теми, тому майже до кожного уроку необхідно робити добірку відповідних історичних або практичних задач. Під час викладання використовувати різні цікаві моменти, історичні довідки, різноманітні форми і методи проведення уроків, що дає можливість підтримувати інтерес учнів до матеріалу теми.

7. Список використаної літератури

1. Бевз Г.П., Алгебра: Проб. підруч. для 7-9 кл. серед. шк. – К.: Освіта, 1996.

2. Бевз Г.П., Методика викладання алгебри. Посібник для вчителів, - К.: «Радянська школа», 1971.

3. Возняк Г.М., Маланюк М.П., Взаємозв’язок теорії з практикою в процесі вивчення математики: Посібник для вчителя. – К.: «Радянська школа», 1989.

4. Гаврилова Н.М., Арифметична та геометрична прогресії //Математика в школах України, 2004, №9, с.11-13.

5. Кірсанова В.О., Прогресія //Математика, 1999, №11,с.6-7.

6. Кочетков Є.С., Кочеткова К.С., Алгебра і елементарні функції, ч.ІІ, - К.: «Радянська школа», 1969.

7. Лоповок Л.М., З досвіду викладання математики в середній школі, - К.: «Радянська школа», 1957.

8. Манько Л.А., Сума перших п членів арифметичної прогресії //Математика в школах України, 2006, №33, с.17-19.

9. Методика преподавания математики в средней школе:Частная методика /Сост. В.И. Мишин, - М.: Просвещение, 1987.

10. Шепель Н.В., Числові послідовності //Математика, 2000, №47, с.4-6.

Дата добавления: 2014-01-11