Розділ 3 хвильова оптика

Cent; W

Б

t

Рисунок 29.1 – а) – Графік биття, побудований для графік змін амплітуди

w / Dw = 10, і б) –

Множник у дужках у формулі (29.1) змінюється набагато повільніше, ніж інший

множник. Через умову

Dw << w

протягом часу, за який

cos w t

робить кілька повних

коливань, множник у дужках майже не змінюється. Це дає підставу розглядати процес (29.1) як майже гармонічне коливання частоти w, амплітуда якого змінюється за деяким періодичним законом. Множник, що знаходиться у дужках, не може виражати закон зміни

амплітуди, тому що він змінюється в межах від

- 2 A до

+ 2 A, у той час як амплітуда за

визначенням є додатною величиною. Графік амплітуди подано на рис. 29.1 б. Аналітичний вираз амплітуди має такий вигляд:

амплітуда =

2 A cos Dw t. (29.2)

2

Цей вираз є періодичною функцію із частотою, яка у два рази перевищує частоту

гармонічної функції, що знаходиться під знаком модуля, тобто із частотою Dw

(див.

рис. 29.1 б). Отже, частота пульсацій амплітуди – її називають частотою биття – дорівнює

різниці частот коливань, що складаються.

Зазначимо, що множник

2 A cos(Dw / 2) t

не тільки визначає амплітуду, але й впливає

на фазу коливання. Це проявляється, наприклад, у тому, що відхилення, які відповідають

сусіднім максимумам амплітуди, мають протилежні знаки (див. точки рис. 29.1 а).

M 1 й M 2 на

§ 30 Додавання взаємно перпендикулярних коливань. Фігури Ліссажу [5]

1 Припустимо, що є дві взаємно перпендикулярні векторні величини x й y, що змінюються з часом з однаковою частотою w за гармонічним законом

....

x = exA cos w t,

..

y = eyB cos(w t + a). (30.1)

Тут ex

і ey

– орти координатних осей X і Y, A і B – амплітуди коливань. Величинами x й

y можуть бути, наприклад, зміщення матеріальної точки від положення рівноваги або

.

напруженості двох взаємно перпендикулярних електричних полів (Ex

У випадку частинки, яка коливається, величини

.

і E y) і т.п.

x = A cos w t,

y = B cos(w t + a)

(30.2)

визначають координати частинки на площині XY. У випадку електричних полів величини

.

(30.2) визначають координати кінця результуючого вектора напруженості поля E.

.

Частинка або кінець вектора E

будуть рухатися по деякій траєкторії, вид якої

залежить від різниці фаз обох коливань a. Вирази (30.2) фактично задають у параметричній формі рівняння цієї траєкторії. Щоб отримати рівняння траєкторії у звичайному вигляді,

потрібно виключити з рівнянь (30.2) параметр t. З першого рівняння випливає, що

Звідси

cos w t =

x. (30.3)

A

sin w t = ±

1- x. (30.4)

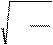
A 2

Розкладемо косинус у другому рівнянні (30.2) за формулою для косинуса суми:

cos(w t + a) = cos w t cos a - sin w t sin a,

підставляючи при цьому замість отримаємо

y

cos w t

x

і sin w t

їх значення (30.3) і (30.4). У результаті

x 2

= cos a ± sin a

B A

1-.

A 2

Це рівняння за допомогою простих перетворень можна звести до вигляду

x + y

- 2 xy cos a = sin 2 a. (30.5)

A 2 B 2 AB

Ми отримали рівняння еліпса, осі якого повернуті відносно координатних осей X і Y.

Орієнтація еліпса і його півосі залежать від амплітуд A і B й різниці фаз a.

2 Проведемо дослідження отриманого результату (30.5). Визначимо форму траєкторії для ряду окремих випадків.

1 Різниця фаз a дорівнює нулю. У цьому випадку рівняння (30.5) спрощується таким чином:

Звідси отримуємо рівняння прямої:

-

æ x y ö

ç ÷

è A B ø

= 0.

y = B x. (30.6)

A

Результуючий рух є гармонічним коливанням уздовж цієї прямої із частотою w й

амплітудою, як дорівнює

A 2 + B 2

(рис. 30.1 а).

2 Різниця фаз a дорівнює

± p. Рівняння (30.5) набуває вигляду

+

æ x y ö

ç ÷

è A B ø

= 0.

Отже, результуючий рух є гармонічним коливанням уздовж прямої

y = - B x

A

(30.7)

(рис. 30.1 б).

Y A A Y

B B

0 X 0 X

B B

A A

а б

Рисунок 30.1 – Траєкторії частинки при різниці фаз, яка дорівнює нулю (а)

і ± p (б)

3 При

a = ±p / 2

рівняння (30.5) переходить у рівняння еліпса, приведеного до

координатних осей:

x 2 y 2

+

A 2 B 2

Y

B

= 1. (30.8)

a = - p

A 1

0 X

a = + p

Рисунок 30.2 – Траєкторія частинки при різниці фаз a = ±p / 2

Півосі еліпса дорівнюють відповідним амплітудам коливань. При рівності амплітуд A і B

еліпс перетворюється у коло.

Випадки

a = +p / 2 й

a = -p / 2

відрізняються напрямом руху по еліпсу або колу. Якщо

a = +p / 2, рівняння (30.2) можна записати таким чином:

x = A cos w t,

y = - B sin w t. (30.9)

У момент t = 0 тіло знаходиться у точці 1 (рис. 30.2). У наступні моменти часу координата x зменшується, а координата y стає від’ємною. Отже, рух відбувається за годинниковою стрілкою.

При a = -p / 2

рівняння (30.2) мають вигляд

x = A cos w t,

y = B sin w t.

Звідси робимо висновок, що рух відбувається проти годинникової стрілки. Зі сказаного випливає, що рівномірний рух по колу радіуса R з кутовою швидкістю w може бути поданий як сума двох взаємно перпендикулярних коливань:

x = R cos w t,

y = ± R sin w t

(30.10)

(знак плюс у виразі для y відповідає руху проти годинникової стрілки, знак мінус – руху за годинниковою стрілкою).

3 У випадку, коли частоти взаємно перпендикулярних коливань відрізняються на

дуже малу величину

Dw, їх можна розглядати як коливання однакової частоти, але з

повільно змінною різницею фаз. Дійсно, рівняння коливань можна подати у вигляді

x = A cos w t,

y = B sin[w t + (Dw t + a)]

і вираз

Dw t + a

розглядати як різницю фаз, що повільно змінюється з часом за лінійним

законом. Результуючий рух у цьому випадку відбувається по повільно змінній кривій, яка

буде послідовно набирати форми, що відповідає всім значенням різниці фаз від

- p до + p.

4 Якщо частоти взаємно перпендикулярних коливань не однакові, то траєкторії

результуючого руху мають вигляд досить складних кривих, які називаються фігурами Ліссажу. На рис. 30.3 і рис. 30.4 наведені приклади таких фігур. Іноді фігурами Ліссажу називають також і траєкторії (зокрема, еліптичні криві), які виникають при складанні взаємно перпендикулярних коливань однакової частоти.

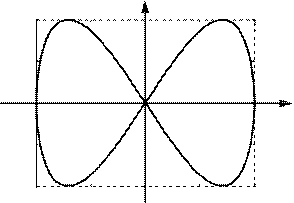Y Y

0 X 0 X

Рисунок 30.3 – Фігура Ліссажу для

Рисунок 30.4 – Фігура Ліссажу для

відношення частот 1:2 і різниці фаз

p / 2

відношення частот 3:4 і різниці фаз

p / 2

§ 31 Диференціальне рівняння загасаючих коливань [5]

У всякій реальній коливальній системі завжди є або сила тертя (у механічній системі), або активний електричний опір (у коливальному контурі), дія яких приводить до зменшення енергії системи. Якщо зменшення енергії не компенсується, то коливання будуть загасати.

1 Розглянемо механічні загасаючі коливання. У найпростішому випадку сила тертя

(наприклад, сила в’язкого тертя) пропорційна швидкості:

Fx = - rx ÿ. (31.1)

Тут r – стала, яку ми будемо називати коефіцієнтом тертя. Знак мінус обумовлений тим,

.

що сила F

й швидкість u спрямовані у протилежні сторони, внаслідок чого їх проекції на

вісь X мають різні знаки.

Рівняння другого закону Ньютона за наявності сили тертя має вигляд

m ÿ x ÿ = - kx - rx ÿ. (31.2)

Використаємо позначення

b = r /(2 m),

w2= k / m, (31.3)

і напишемо рівняння (31.2) у вигляді

ÿ x ÿ+ 2b x ÿ + w2 x = 0. (31.4)

Відзначимо, що величину b в (31.4) називають коефіцієнтом загасання; w0

є власною

частотою коливальної системи, тобто та частота, з якої коливалася б система за умови відсутності тертя. Таким чином, отримали диференціальне рівняння (31.4), що визначає поведінку коливальної величини x за наявності сили тертя. Це рівняння називають диференціальним рівнянням загасаючих коливань.

2 Розглянемо загасаючі електричні коливання. Нехай у коливальному контурі, крім ємності C й індуктивності L, є активний опір R (рис. 31.1). Застосуємо закон Ома для ділянки кола 1-3-2 (див. рис. 31.1):

IR = j1- j2+ E s. (31.5)

Різницю потенціалів на конденсаторі визначимо зі співвідношення

j1- j2= q 1/ C = (- q)/ C. (31.6)

Тут використали, що заряд пластини конденсатора 1 q 1= - q

Сила струму I є додатною, коли напрям струму збігається з напрямом обходу ділянки кола 1-3-2, тобто за

годинниковою стрілкою. У цьому разі заряд на пластині

(див. рис. 31.1).

C

+ q - q

2 1

конденсатора q 2 = q

пов’язаний із силою струму в ділянці

кола таким співвідношенням: R

I = + dq / dt = + q ÿ. (31.7) I

Знак «+» обумовлений тим, що, коли струм I є додатним,

заряд q 2 = q

збільшується (q ÿ > 0). L

Підставимо в (31.5) закон самоіндукції

E s = - L dI / dt, співвідношення (31.6) й (31.7) й отримаємо

Рисунок 31.1

Далі вводимо позначення

Rq ÿ = - q / C - L q ÿÿ. (31.8)

b = R /(2 L),

w2= 1/(LC), (31.9)

і перетворюємо рівняння (31.8) до такого вигляду:

q ÿÿ + 2b q ÿ + w2 q = 0. (31.10)

Отримане рівняння подібне до (31.4), яке описує механічні коливання, і має таку саму назву:

диференціальне рівняння загасаючих коливань. Величину b в (31.10), як і у випадку

механічної системи, називають коефіцієнтом загасання; w0

є власною частотою

контуру, тобто та частота, з якої відбувалися б коливання за умови відсутності активного опору. Таким чином, отримали диференціальне рівняння (31.10), що визначає поведінку коливальної величини q за наявності активного опору в коливальному контурі.

Із порівняння формул (31.3) і (31.9) випливає, що опір R відіграє роль коефіцієнта тертя r, індуктивність L – роль маси, величина, що зворотна ємності C, – роль коефіцієнта квазіпружної сили k.

§ 32 Розв’язання диференціального рівняння загасаючих коливань. Коефіцієнт загасання, декремент загасання, логарифмічний декремент загасання, добротність [5]

1 Знайдемо розв’язок диференціального рівняння гармонічних коливань:

ÿ x ÿ+ 2b x ÿ + w2 x = 0. (32.1)

У цьому рівнянні b – коефіцієнт загасання; w0

– власна частота коливальної системи (тобто

та частота, з якою коливалася б система за умови відсутності загасання). Величина x може бути механічним зміщенням частинки, електричним зарядом на конденсаторі й т.д.

Коефіцієнти b та w0

визначаються параметрами коливальної системи.

Будемо шукати розв’язок рівняння (32.1) у вигляді

x = u exp(- b t), (32.2)

де u – деяка, поки що невідома, функція від t. Диференціювання функції x (32.2) за змінною t дає

x ÿ = u ÿ exp(- b t)- u b exp(- b t) = (u ÿ - b u)exp(- b t),

ÿ x ÿ = (u ÿÿ - b u ÿ)exp(- b t)- (u ÿ - b u)b exp(- b t) = (u ÿÿ - 2b u ÿ + b2 u)exp(- b t).

Після підстановки виразів для x, x ÿі

ÿ x ÿ у рівняння (32.1) і скорочення на відмінний від нуля

множник exp(- b t) отримаємо диференціальне рівняння для u:

u ÿÿ+ (w2 - b2) u = 0. (32.3)

Розв’язання рівняння (32.3) залежить від знака X

коефіцієнта, що стоїть біля u. Розглянемо

випадок, коли цей коефіцієнт є додатним (тобто

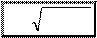b < w0). Введемо позначення A 0

A 0exp(-b t)

w = w2- b2

, (32.4)

A ¢ A ¢ A ¢

і отримаємо рівняння

0 t

u ÿÿ+ w2 u = 0. (32.5)

Рівняння (32.5) є диференціальним рівняння гармонічних коливань і тому його розв’язок можемо записати у вигляді

u = A 0cos(w t + a),

де w є частотою загасаючих коливань (див.

T

Рисунок 32.1 – Графік загасаючого коливання. Верхня штрихова крива – графік зміни амплітуди з часом

також (32.4)). Далі підставляємо отриманий вираз для u в (32.2) і знаходимо у випадку малого тертя (b < w0) розв’язок диференціального рівняння загасаючих коливань (32.1):

x = A e -b t cos(w t + a). (32.6)

Тут

A 0 і a – сталі, значення яких залежать від початкових умов, w – частота загасаючих

коливань, що визначається формулою (32.4).

2 Проведемо дослідження отриманого результату (32.6), з’ясуємо характеристики загасаючих коливань. Графік функції (32.6) наведений на рис. 32.1. Штриховими лініями показані межі, у яких знаходиться зміщення змінної величини x.

Відповідно до виду функції (32.6) величину x можна розглядати як квазігармонічне коливання частоти w з амплітудою, що змінюється за законом

A (t) = A e -b t. (32.7)

Величину (32.7) називають амплітудою загасаючих коливань. Верхня зі штрихових кривих

на рис. 32.1 дає графік цієї функції, причому

A 0є амплітудою в початковий момент часу.

Розглянемо послідовні найбільші відхилення величини x (вони відбуваються через

період загасаючих коливань T), наприклад, A ¢, A ¢¢, A ¢¢¢

і т.д. на рис. 32.1. Неважко

з’ясувати, що відношення двох послідовних найбільших відхилень мають одне й те саме

значення. Дійсно, коли

A ¢= A 0exp(- b t), то

A ¢ =

A ¢¢

A 0exp[- b(t)]

A 0exp[- b(t + T)]

= exp(b T),

A ¢¢ =

A ¢¢¢

A 0exp[- b(t + T)]

A 0exp[- b(t + 2 T)]

= exp(b T)

і т.д. Це означає, що таке відношення може бути характеристикою загасаючого коливання. Таким чином, відношення значень амплітуди, що відповідають моментам часу, що відрізняється на період, дорівнює

A (t)

A (t + T)

= exp(b T).

Це відношення називають декрементом загасання, а його логарифм – логарифмічним декрементом загасання:

æ A (t) ö

()

l = lnç ÷ = b T. (32.8)

A t + T

è ø

Відповідно до формули (32.4) період загасаючих коливань відрізняється від періоду вільних коливань:

T = 2p /

w2- b2

. (32.9)

При незначному терті (b2<< w2) період коливань практично дорівнює періоду вільних коливань T 0= 2p / w0. Зі збільшенням коефіцієнта загасання період коливань зростає.

Для характеристики коливальної системи використовується також величина

Q = p / l, (32.10)

яка називається добротністю коливальної системи.

З'ясуємо фізичний зміст коефіцієнта загасання b. Знайдемо час t, за який амплітуда

зменшується в e раз. З визначення величини t випливає, що e -bt= e -1, звідки bt = 1. Отже, коефіцієнт загасання b є оберненим до проміжку часу t, за який амплітуда зменшується в e разів ( b = 1/ t ). У цьому й полягає фізичний зміст коефіцієнта загасання.

З’ясуємо фізичний зміст логарифмічного декременту загасання l. Виразивши відповідно до (32.8) b через l і T, можна закон зменшення амплітуди з часом написати у вигляді

A (t) =

A e -(l / T) t.

Час t, за який амплітуда зменшується в e раз, система встигає виконати

Ne = t / T

коливань.

З умови

exp(- lt / T) = exp(-1) маємо, що

lt / T = l Ne = 1. Отже, логарифмічний декремент

загасання є оберненим до числа коливань, за час яких амплітуда зменшується в e разів

( l = 1/ Ne). У цьому полягає фізичний зміст логарифмічного декремента загасання.

Фізичний зміст добротності полягає у тому, що вона прямо пропорційна числу коливань, за час яких амплітуда зменшується в e разів (Q = p / l = p Ne).

§ 33 Диференціальне рівняння вимушених коливань та його розв’язання [5]

1 Розглянемо механічну коливальну систему із загасанням, яка знаходиться під дією зовнішньої сили, що змінюється з часом за гармонічним законом:

Fx = F 0cos W t. (33.1)

Під дією зовнішньої періодичної сили в системі виникають вимушені коливання. Знайдемо диференціальне рівняння, яке описує вимушені коливання. Для цього застосуємо другий закон Ньютона:

Увівши позначення

m ÿ x ÿ = - kx - rx ÿ + F 0 cos W t.

b = r /(2 m),

перетворимо рівняння до такого вигляду:

w2= k / m,

ÿ x ÿ+ 2b x ÿ + w2

x = (F 0/ m)cos W t. (33.2)

Тут b – коефіцієнт загасання; w0

– власна частота коливальної системи; W – частота

зовнішньої періодичної сили. Рівняння (33.2) описує вимушені коливання й називається

диференціальним рівнянням вимушених коливань.

2 Розглянемо вимушені електричні коливання у коливальному контурі з активним

опором. Підключимо до коливального контуру з ємністю C, індуктивністю L й активним опором R зовнішнє джерело змінної напруги:

U = U m cos W t

(33.3)

(див. рис. 33.1). Під дією зовнішньої змінної напруги у контурі виникають вимушені коливання. Отримаємо диференціальне рівняння, яке описує процеси у контурі. Для цього застосуємо закон Ома для ділянки кола 1-3-2 (див. рис. 33.1):

IR = j1- j2+ E. (33.4)

Слід зазначити, що змінну напругу зовнішнього джерела U тут потрібно враховувати разом з ЕРС самоіндукції. Тобто загальна ЕРС, яка діє в контурі, дорівнює

E = E s + U = - L dI / dt + U. (33.5)

Різницю потенціалів на конденсаторі визначимо зі співвідношення

C

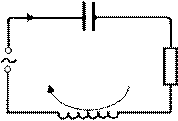I + q - q

j1- j2= q 1/ C = (- q)/ C. (33.6) 2 1

Тут використали, що заряд пластини конденсатора 1 U R

q 1= - q

(див. рис. 33.1).

Сила струму I є додатною, коли напрям струму 3

збігається з напрямом обходу ділянки кола 1-3-2, тобто за

годинниковою стрілкою.У цьому разі заряд на пластині L

конденсатора

q 2 = q

пов’язаний із силою струму в Рисунок33.1

ділянці кола таким співвідношенням:

I = + dq / dt = + q ÿ. (33.7)

Знак «+» обумовлений тим, що, коли струм I є додатним, заряд q 2 = q

збільшується (q ÿ > 0).

Підставимо у (33.4) співвідношення (33.5)-(33.6) з урахуванням (33.7) та (33.3) й

отримуємо

Далі вводимо позначення

Rq ÿ = - q / C - L q ÿÿ + Um cos W t. (33.8)

b = R /(2 L),

w2= 1/(LC), (33.9)

і перетворюємо рівняння (33.8) до такого вигляду:

q ÿÿ + 2b q ÿ + w0 q = (U m / L)cos W t. (33.10)

Тут b – коефіцієнт загасання; w0

– власна частота коливального контуру; W – частота

коливань зовнішнього джерела. Рівняння (33.10) описує вимушені коливання й називається

диференціальним рівнянням вимушених коливань.

Порівнявши диференціальне рівняння вимушених коливань для механічної системи (33.2) та для електричного коливального контуру (33.10), можемо зробити висновок, що вони є з математичної точки зору однаковими.

3 Знайдемо розв’язок диференціального рівняння вимушених коливань (33.10) (такий

самий розв'язок буде й для рівняння (33.2)).

Рівняння типу (33.10) називають неоднорідними диференціальними рівняннями з сталими коефіцієнтами. З теорії лінійних диференціальних рівнянь із сталими коефіцієнтами

відомо, що загальний розв’язок неоднорідного рівняння (тобто рівняння, у правій частині

якого стоїть функція від t, яка не дорівнює тотожно нулю) дорівнює сумі загального розв’язку відповідного однорідного рівняння (тобто того ж рівняння, у якому права частина дорівнює тотожно нулю) і частинного розв’язку неоднорідного рівняння. Загальний розв’язок однорідного рівняння ми вже знаємо (розв’язок диференціального рівняння загасаючих коливань). Воно має вигляд

q = q e -b t cos(w t + a), (33.11)

де w =

w2- b2

– частота загасаючих коливань.

Залишається тепер знайти частинний (який не має довільних сталих) розв’язок рівняння (33.10). Будемо шукати цей розв’язок у вигляді

q = A cos(W t - j), (33.12)

де j – зсув фаз між зовнішньою напругою і викликаними нею коливаннями в контурі. Спробуємо з'ясувати, чи не існує таких значень A і j, при яких функція (33.12) задовольняє рівняння (33.10). Для цього підставимо у рівняння (33.10) вираз (33.12) і його похідні:

q ÿ = - A W sin (W t - j), (33.13)

q ÿÿ = - A W2 cos(W t - j), (33.14)

розвертаючи одночасно різниці:

sin (W t - j) й

cos(W t - j)

за формулами для синуса й косинуса

- A W2[cos j cos W t + sin jsin W t ]- 2b A W[cos j sin W t - sin j cos W t ]+

+ w2

A [cos j cos W t + sin jsin W t ]= (U m / L)cos W t.

Згрупувавши відповідним чином члени рівняння, отримаємо

[ A (w2- W2)cos j + 2b A W sin j]cos W t - [ A (w2- W2)sin j - 2b A W cos j] sin W t = (U

0 0 m

/ L)cos W t.

(33.15)

Для того щоб рівняння (33.15) задовольнялося при будь-яких значеннях t,

коефіцієнти при

cos W t

й sin W t

в обох частинах рівняння повинні бути однаковими. Звідси

знаходимо умови:

A (w2

- W2

)cos j + 2b A W sin j = (U m / L), (33.16)

A (w2- W2)sin j - 2b A W cos j = 0. (33.17)

Із цих співвідношень можна знайти значення A й j, при яких функція (33.11) задовольняє рівняння (33.10). Піднісши рівності (33.16) і (33.17) у квадрат і склавши їх один з одним, отримаємо

m

звідки

A 2(w2- W2)2+ 4b2 A 2W2= (U

/ L)2,

A = Um / L

(2 2)2

. (33.18)

2 2

З рівняння (33.17) випливає, що

w0- W

+ 4b W

tg j =

2bW w2- W2

. (33.19)

Підставивши в (33.12) значення A й j, які визначаються формулами (33.18) і (33.19),

отримуємо частинний розв’язок неоднорідного рівняння (33.10):

q = Um / L

æ

ç

c W t - arctg

2bW

ö

. (33.20)

(w - W

) + 4b W

osç

÷

w2- W2÷

2 2 2

2 2 è 0 ø

Функція (33.20) у сумі з (33.11) дає загальне розв’язання рівняння (33.10). Доданок

(33.11) відіграє помітну роль тільки на початковій стадії процесу, при встановленні коливань.

Із часом через експонентний множник

exp(- b t)

роль доданка (33.11) зменшується, і через

деякий час ним можна знехтувати, зберігши в розв’язку тільки доданок (33.20).

Таким чином, співвідношення (33.20) описує усталені вимушені коливання.

§ 34 Резонанс. Резонансна частота [5]

1 Резонанс напруги (зміщення). Як відомо, усталені вимушені коливання заряду конденсатора

C

I + q - q

коливального контуру (рис. 34.1) описуються рівнянням 2 1

q = A cos(W t - j), (34.1)

U R

де

A = Um / L

(2 2)2

, (34.2) 3

2 2

w0- W

+ 4b W L

tg j = 2bW. (34.3) Рисунок 34.1

w2- W2

У цих рівняннях Um, W – амплітуда напруги і частота зовнішнього джерела змінної напруги, w0, b, L є відповідно власна частота, коефіцієнт загасання й індуктивність коливального контуру.

Проведемо дослідження амплітуди вимушених коливань A (див. (34.2)) залежно від

частоти вимушених коливань W. Залишаючи амплітуду Um

зовнішнього джерела

постійною, будемо змінювати його частоту W. При W = 0 отримаємо під дією постійної

напруги статичне відхилення

q 0. При зростанні частоти W амплітуда A також зростає, має

різкий максимум в області частот, які близькі до власної частоти коливальної системи потім асимптотично прямує до нуля (рис. 34.1).

Явище різкого зростання амплітуди

w0,

вимушених коливань у коливальній системі, що відбувається при наближенні частоти A

періодичного зовнішнього впливу W до власної

b1< b2< b3

b1

частоти системи

w0, називається резонансом.

Частота, при якій має місце максимум, називається резонансною частотою. Сукупність графіків функції (34.2), що зображена на рис. 34.1, називається резонансними кривими. Про резонанс заряду на конденсаторі зазвичай говорять як про резонанс напруги тому, що заряд і напруга на конденсаторі пов’язані між собою прямо пропорційно (UC = q / C). Резонансу напруги у механічній моделі відповідає резонанс зміщення.

Щоб визначити резонансну частоту у

b2

b3

q 0

0 W

w

W рез 0

випадку резонансу напруги

W рез, потрібно знайти

Рисунок 34.2 – Резонансні криві для

заряду конденсатора (зміщення)

максимум функції (34.2) або мінімум виразу, що

стоїть під коренем (34.2) у знаменнику. Продиференціювавши цей вираз за W й прирівнявши

отриману похідну до нуля, отримаємо умову, що визначає резонансну частоту W рез:

- 4(w2- W2)W + 8b2W = 0.

Це рівняння має три розв’язки:

W = 0

і W = ±

w2- 2b2. Розв’язок, що дорівнює нулю,

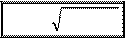відповідає максимуму знаменника (тобто мінімуму амплітуди). З інших двох розв’язків, що є від’ємним, потрібно відкинути, як такий, що не має фізичного змісту (частота не може бути від’ємною). Таким чином, для резонансної частоти отримуємо

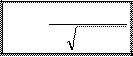
W рез =

w2- 2b2

. (34.4)

Підставивши це значення в (34.2), знаходимо вираз для амплітуди при резонансі:

Aрез

= U m / L

2b w2- b2

. (34.5)

Із цього виразу випливає, що за умови відсутності опору (тертя) (b = 0) амплітуда при резонансі дорівнювала б нескінченності. Згідно з (34.4) резонансна частота за тих самих умов (при b = 0) збігалася б із власною частотою коливань системи w0.

Знайдемо відношення амплітуди при резонансі ( W = W рез) до амплітуди, коли

частота зовнішнього впливу дорівнює нулю ( W = 0 ). При прямуванні частоти до нуля заряд

на конденсаторі дорівнює, як це випливає з (34.2),

q 0 = U m /(L w0)= CU m

(тут використали,

що W = 0,

w2= 1/(LC)). Це значення відповідає заряду на конденсаторі, який виникає під

дією постійної напруги

Um. З іншого боку, відповідно до формули (34.5) при малому

загасанні (тобто при b << w0) амплітуда при резонансі дорівнює

» m

U / L

Aрез.

= U m /(L w

q

2bw0

Розділимо цей вираз на величину заряду на конденсаторі

0 0)= CU m, що виникає

при постійній зовнішній напрузі. У результаті отримаємо, що

Aрез

» w0=

2p =

p

= Q. (34.6)

q 0 2b

2b T l

Таким чином, добротність показує, у скільки разів амплітуда заряду конденсатора при резонансі перевищує заряд, що виникає на конденсаторі під дією постійної напруги, модуль якої дорівнює амплітуді змінної напруги.

2 Резонанс струмів (швидкості). Для

електричного струму у коливальному контурі також має I m місце явище резонансу і про це явище говорять як про резонанс струмів (для механічної моделі – резонанс швидкості).

Знайдемо резонансну частоту для резонансу струмів. Виходячи з (34.1) неважко отримати вираз для електричного струму в коливальному контурі під час усталених вимушених коливань:

I = q ÿ = - A W sin(W t - j) = Im cos(W t - j + p / 2), (34.7)

b1< b2< b3

b1

b2

b3

де

I = W U m / L =

U m / L

m. (34.8)

W рез = w0

(2 2)2

2 2 (2

2)2 2 2

w0- W

+ 4b W

w0- W

/ W + 4b

Рисунок 34.3 – Резонансні кри-

З (34.8) випливає, що амплітуда коливань струму має іншу залежність від частоти зовнішнього періодичного джерела

ві для струму у коливальному

контурі (швидкості)

(див. рис. 34.2). Зрозуміло, що при резонансі амплітуда

Im буде максимальною. Максимум

Im буде тоді, коли знаменник (34.8) набуває мінімального значення. Неважко з’ясувати, що

це має місце, коли W = w0. Таким чином, у випадку резонансу струмів (резонансу швидкості) резонансна частота визначається співвідношенням

W¢ рез = w0. (34.9)

§ 35 Закон Ома для змінних струмів. Імпеданс. Ємнісний та індуктивний опори [2]

1 Знайдемо зв’язок між амплітудами змінної напруги та змінного електричного струму у коливальному колі (рис. 34.1). Описані у попередніх параграфах усталені вимушені коливання можна розглядати як проходження у колі, що має ємність C, індуктивність L й активний опір R, змінного струму, який обумовлений змінною напругою

U = U m cos W t. (35.1)

Відповідно до отриманих раніше результатів цей струм змінюється за законом

I = q ÿ = - A W sin (W t - j) = Im cos(W t - j + p / 2) = Im cos(W t - y), (35.2)

де амплітуда струму Im

та фаза y визначаються співвідношеннями:

Im = A W =

Um W / L

(2 2)2

, (35.3)

2 2

w0- W

+ 4b W

2 2

tg y = tg (j - p / 2) = -1/ tg j = - w0- W

2bW

. (35.4)

Коли ж взяти до уваги, що власна частота та коефіцієнт загасання пов’язані з параметрами контуру співвідношеннями

2 1

R

w0= LC, b = 2 L, (35.5)

то для амплітуди сили струму у контурі Im

і фази y можемо записати

Im =	U m
R 2+ (Ω L −1/(Ω C))2

, (35.6)

tg y =

W L -1/(W C)

R

. (35.7)

Формула (35.6) є подібною до закону Ома у тому розумінні, що амплітуда струму Im

пропорційна амплітуді напруги Um. Тому формулу (35.6) іноді називають законом Ома для змінного струму. Однак потрібно пам'ятати, що ця формула встановлює співвідношення лише між амплітудами, але не миттєвими значеннями U і I.

У випадку постійного струму відношення напруги до сили струму визначає опір

провідника. Подібно до цього при змінному струмі відношення амплітуди повної напруги до амплітуди струму

Z = R 2+ (W L -1/(W C))2

(35.8)

називають повним електричним опором, або імпедансом.

2 Усяке реальне електричне коло має скінченні

R, L

й C. В окремих випадках деякі з

цих параметрів бувають такими, що їх впливом на струм можна знехтувати. Проаналізуємо ряд таких випадків.

Розглянемо електричне коло, що складається лише з активного опору R.

Використовуючи закон Ома, можемо знайти силу струму

I = U / R = (U m / R)cos W t = Im cos W t.

Звідси випливає, що струм у цьому випадку змінюється у фазі з напругою, тобто відповідний зсув фаз дорівнює нулю y = 0, а амплітуда сили струму дорівнює

U

Im = m

R

. (35.9)

Порівняння отриманого виразу з (35.6) показує, що заміна конденсатора закороченою

ділянкою кола означає перехід не до

C = 0, а до

C = ¥. Також порівняння показує, що

заміна котушки індуктивності закороченою ділянкою кола означає перехід до

L = 0.

Розглянемо електричне коло, що складається лише з котушки з індуктивністю L. Це

означає, що активним опором кола можна знехтувати при можна покласти такою, що дорівнює нескінченності використовуючи формули (35.6) та (35.7), отримуємо

R = 0, ємність конденсатора

C = ¥. В цьому випадку,

I = U m, (35.10)

m W L

a tg y = +¥

(відповідно y = +p / 2). Величину

X L = W L

(35.11)

називають реактивним індуктивним опором, або просто індуктивним опором кола. Як бачимо, y = +p / 2, тобто напруга на індуктивності випереджає струм на p / 2.

Розглянемо електричне коло, що складається лише з конденсатора з ємністю C. Тобто припускаємо, що можна покласти такими, що дорівнюють нулю, R й L. Тоді відповідно до формул (35.6) та (35.7)

tg y = -¥

(тобто

y = -p / 2). Величину

I = U m, (35.12)

m 1/(W C)

X C = W C

(35.13)

називають реактивним ємнісним опором, або просто ємнісним опором. Оскільки

y = -p / 2, напруга на конденсаторі відстає від струму на p / 2.

3 Як бачимо, на конденсаторі та котушці напруга і струм зміщені за фазою на

p / 2.

Це приводить до того, що середня потужність, яка виділяється на цих елементах, дорівнює нулю. Дійсно,

W 2p / W

W 2p / W

< PC >=< I × UC >= 2p

ò Im cos(W t - (-p / 2)) Um cos(W t) dt = - 4p ImUm

òsin (2W t) dt = 0,

W 2p / W

W 2p / W

< PL >=< I × U L >= 2p

ò Im cos(W t - (+p / 2)) Um cos(W t) dt = 4p ImU m

òsin (2W t) dt = 0.

Саме через цю особливість ємнісний X C

та індуктивний X L

опори називають

реактивними, на конденсаторі та котушці індуктивності тепло не виділяється.

На противагу реактивним опорам

X C та

X L на опорі R струм і напруга змінюються

синфазно. Тому середня потужність, яка виділяється на опорі R, не дорівнює нулю:

2p / W

< P >=< I × U

>= W

ò I cos(W t) U

cos(W t) dt = W I U

× 1 2p = ImUm. (35.14)

R R 2p m m

2p m

m 2 W 2

Саме через цю особливість опір R називають активним, на опорі R виділяється тепло.

Позначимо через

Iеф

та Uеф

силу та напругу постійного струму, який виділяє на

опорі R таку саму середню потужність, що і у випадку змінного електричного струму. Тоді

2 2

< PR >= IефUеф = RIеф = Uеф / R.

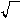Порівнюючи цей вираз із виразом для потужності змінного струму (35.14), можемо записати

Iеф = Im /

2, Uеф = U m /

2. (35.15)

Сила струму

Iеф

з (35.15) називається ефективною (діючою) силою змінного

струму, а Uеф

з (35.15) – ефективною (діючою) напругою.

У загальному випадку середня потужність, яка виділяється на елементах контуру, що складається з котушки індуктивності, конденсатора та опору, визначається таким співвідношенням

< P >=< U × I >=

2p / W

W 2p / W

2p ò Um

cos(W t)× Im

cos(W t - y) dt =

W

= 2p ò

U m × Im (cos(W t + W t - y)+ cos(W t - W t + y)) dt =

2

= ImUm cos(y) = I

ефUеф

cos(y).

Тут використали співвідношення (35.1), (35.2), (35.15). Таким чином, потужність, яка виділяється на елементах електричного контуру, визначається різницею фаз напруги та

струму y (35.7), ефективною силою струму яка подається на контур:

Iеф

у контурі та ефективною напругою Uеф,

< P >= ImUm cos(y) = I

ефUеф

cos(y). (35.16)

4 Використовуючи розглянуті вище властивості окремих елементів контуру можна достатньо легко аналізувати змінні струми і змінні напруги у довільному контурі за допомогою методу векторних діаграм. Розглянемо, наприклад, контур, що зображений на рис. 35.1. З цього

рисунка випливає, що повна напруга U дорівнює сумі напруг

~ U

L R C

U L U R UC

на кожному з елементів контуру:

Зрозуміло, що тут маємо справу гармонічними коливаннями

Рисунок 35.1

U R + UC + U L = U. (35.16)

U

U R, UC, U L

однакової частоти та

W LIm Um

æ 1 ö

напрямку. Тому додавання цих гармонічних коливань проведемо

за допомогою методу векторних

ç W L - ÷ Im

y è W C ø

1 Вісь струмів

діаграм.

Візьмемо до уваги, що електричні

Дата добавления: 2014-01-11