Явление самоиндукции

Рассмотрим теперь второй случай, когда поток магнитной индукции создается током, текущим в самом контуре. По аналогии с предыдущим, запишем сразу:

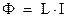(4)

где 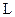‑ коэффициент самоиндукции, или индуктивность контура.

Коэффициент индуктивности (индуктивность) численно равен создаваемому потоку магнитной индукции, если ток в контуре равен единице. Индуктивность также измеряется в генри.

Найдем выражение для коэффициента самоиндукции.

Рассмотри соленоид с числом витков 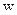. Действие соленоида самого на себя, должно быть таким же, как действие этого соленоида на другой соленоид, точно такой же. Отсюда, используя значение коэффициента взаимной индукции двух катушек трансформатора, мы получим значение коэффициента самоиндукции соленоида, полагая :

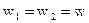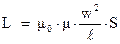(5)

Следовательно, выражение для ЭДС самоиндукции будет иметь вид:

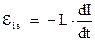(6)

Из (6) вытекает: если 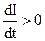, то 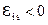. И наоборот, если 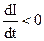, то 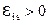. Т.е. ЭДС самоиндукции тормозит изменение тока, вызванного внешними причинами, т.е. сторонними силами, в том числе и сопротивлением контура.

Таким образом, наличие индуктивности приводит к тому, что контур приобретает своего рода электромагнитную инертность, которая выражается в том, что любое изменение тока тормозится тем быстрее, чем больше индуктивность 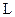контура.

При постоянном токе индуктивность не проявляется.

Рассмотрим теперь математически высказанные замечания.

Пусть имеется контур с индуктивностью 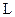, как показано на рис. 8.

Если ключ перевести в верхнее положение, то ток в цепи будет нарастать, следовательно, появится ЭДС самоиндукции. При достижении током своего номинального значения, он перестанет изменяться и ЭДС самоиндукции станет равной нулю 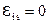, а ток 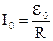. Если теперь ключ перевести в нижнее положение (тем самым мы исключаем 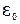), то ток в цепи будет уменьшаться. Но появится ЭДС самоиндукции, препятствующая уменьшению тока. На основании второго правила Кирхгофа можно записать:

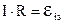
Подставляя сюда выражение для ЭДС самоиндукции (3.34), получим:

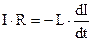
Преобразуем полученное выражение:

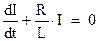
Интеграл этого дифференциального уравнения имеет вид:

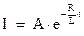
Значение константы 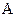найдется из начального условия: в момент времени 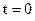, ток был 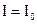. Отсюда получаем ‑ 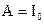, и соответственно окончательное выражение зависимости силы тока от времени:

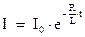
Отношение 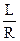должно иметь размерность времени. Действительно, размерность индуктивности ‑ генри 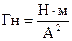. Размерность сопротивления ‑ Ом, 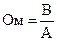. Следовательно, 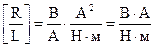. Но размерность вольта 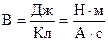. Поэтому для искомой размерности получаем: 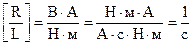, или 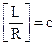. Исходя из этого, обозначим отношение 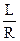через 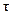‑ 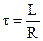. В этом случае, закон убывания тока в цепи, будет иметь следующий вид:

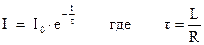(7)

Отсюда вытекает физический смысл 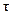‑ время релаксации, время, в течение которого сила тока в цепи уменьшится в 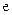раз (по аналогии с затухающими колебаниями).

Таким образом, зная параметры контура, можно сразу рассчитать время релаксации.

Рассмотрим теперь случай нарастания тока, т.е. случай, когда ключ находится в верхнем положении (см. рис. 3.31). С учетом второго правила Кирхгофа, запишем:

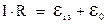
Преобразуя это уравнение с учетом (3.34) получим:

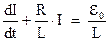
Частное решение этого уравнения возьмем в виде ‑ 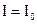. Общее решение соответствующего однородного уравнения мы уже получили ‑ 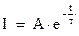. Поэтому общее решение дифференциального уравнения нарастания тока в цепи будет иметь вид:

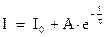
Константу интегрирования 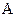найдем из начальных условий: в начальный момент времени 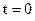сила тока равнялась нулю 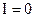. Из этого условия получим, что 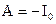. И уравнение нарастания тока в цепи будет иметь следующий вид:

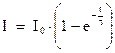(8)

При рассмотрении возрастания и убывания тока, мы считали цепь замкнутой. Если просто разорвать цепь, то величина возникшей ЭДС самоиндукции может быть очень велика, так что между контактами выключателя возникает электрический разряд. При этом развиваются значительные токи. Это явление получило название экстратоки размыкания.

Лекция 2. (2 часа)

Дата добавления: 2014-01-11