Расчет реактивной силы (тяги)

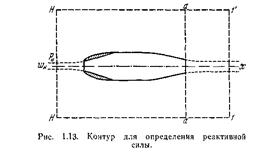Для нахождения величины реактивной силы Р нет необходимости рассматривать детально распределение давления по внутренним и наружным стенкам реактивного аппарата. Реактивную силу можно определить в конечном виде с помощью уравнения количества движения. Совершая полет, тело производит возмущение в окружающей среде. Всегда можно выделить некоторую, достаточно большую, например цилиндрическую, область, границы которой выходят за пределы возмущенной части потока (рис.). На боковых границах этой области давление и скорость потока (считаем двигатель неподвижным, а воздух движущимся со скоростью полета) равны их значениям на бесконечности перед двигателем. Пусть ось х совпадает с направлением полета и является осью симметрии двигателя; спроектируем на ось х силы, действующие на двигатель и на поверхность выделенного контура. Так как силы давления в жидкости нормальны к поверхности, то проекции на ось х сил, действующих на боковые поверхности контура, обращаются в нуль. Поэтому уравнение Эйлера запишется так:

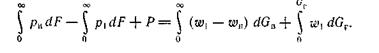
Здесь площади, на которые распространяются интегралы, и область интегрирования первого члена правой части бесконечны. Сила Р берется со знаком + потому, что здесь реактивный двигатель сообщает работу газу; 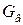− секундная масса воздуха, втекающая в контур через сечение F; 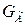− дополнительная секундная масса горючего, которая подается в двигатель.

Если взять левую торцовую поверхность далеко перед двигателем, то давление на ней постоянно и равно атмосферному (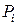), а скорость потока равна скорости полета (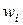). Кроме того, можно допустить, что в поперечном направлении уже на некотором конечном расстоянии от поверхности двигателя поток является невозмущенным и площадь F, на которую распространяются интегралы левой части, считать конечной; точно так же конечной будет и область интегрирования в первом члене правой части. Тогда следует написать:

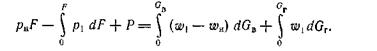
В большом числе случаев возмущение, вызываемое летящим телом, настолько незначительно, что в плоскости среза сопла а (вне струи выхлопных газов) давление обтекающего потока мало отличается от давления на бесконечности (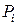). Тогда силы давления на передней и задней торцовых поверхностях контура уравновешиваются везде, кроме участка, соответствующего поперечному сечению выхлопной струи (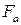). Скорости потока во всех элементарных струйках, кроме проходящих через двигатель, одинаковы (пренебрегаем влиянием трения, вихревых и волновых потерь на наружной поверхности двигателя). Следовательно, изменение количества движения получается только в струе, протекающей сквозь двигатель. Тогда уравнение Эйлера принимает следующий вид:

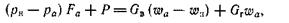
откуда получается основная формула для реактивной силы

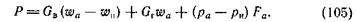
В этих выражениях 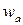− средняя скорость истечения.

Следует подчеркнуть, что полученное соотношение справедливо только в том случае, если скорость и давление в плоскости а (за исключением участка рабочей струи) равны в точности их значениям на бесконечности перед двигателем. Кроме того, мы здесь пренебрегаем внешним лобовым сопротивлением двигателя, которое всегда может быть учтено отдельно.

На расчетном режиме работы реактивного двигателя давление в выхлопной струе равно давлению окружающего воздуха (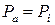); в этом случае тяга равна изменению количества движения газа, прошедшего через двигатель:

В воздушно-реактивных двигателях второй член правой части мал, и им часто пренебрегают, т.е. принимают для воздушно-реактивных двигателей в расчетном случае

Тяга жидкостного реактивного двигателя, в котором не используется атмосферный воздух, определяется для расчетного режима по формуле

или на нерасчетном режиме

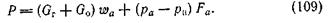
Здесь GO — секундный массовый расход окислителя.

О месте приложения реактивной силы.

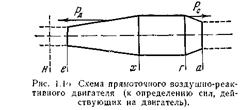
Выясним, в каком месте двигателя приложена реактивная сила. Рассмотрим простейший случай − идеальный прямоточный воздушно-реактивный двигатель (рис.). Пусть скорость во входном отверстии равна скорости полета (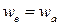); тогда давление во входном отверстии равно атмосферному (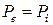), кроме того, предположим, что двигатель работает на расчетном режиме, т. е. давление в выходном отверстии также равно атмосферному (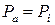). При малой скорости движения газа в камере сгорания давление в последней можно считать постоянным (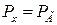). В описанном идеальном двигателе перепады давлений в диффузоре и сопле одинаковы: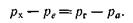

Однако ввиду того, что в сопле воздух имеет более высокую температуру, чем в диффузоре, площадь выходного отверстия двигателя должна быть больше площади входного отверстия. В самом деле, в идеальном двигателе скоростной напор в выходном отверстии равен скоростному напору набегающего потока, т.е. в рассматриваемом случае скоростному напору во входном отверстии

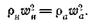
С учетом этого равенства, из уравнения неразрывности получаем:

Следовательно, при подводе тепла в камере сгорания (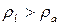) имеем:

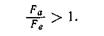
Итак, среднее давление, действующее на стенки диффузора и сопла, одно и то же, а проекция стенки диффузора на плоскость, перпендикулярную к оси двигателя, больше соответствующей проекции стенки сопла. Вследствие изложенного сила давления изнутри на диффузор () больше, чем на сопло (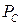); направления этих сил, как явствует из рис., противоположны.

Если внешние очертания двигателя являются очень плавными, то давление воздуха на внешнюю поверхность двигателя весьма близко к атмосферному, т. е. силой давления на внешнюю поверхность можно пренебречь. В рассматриваемом идеальном случае реактивная сила, действующая на двигатель, сводится к разности сил, приложенных соответственно к диффузору и соплу:

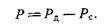
Величины сил, действующих на диффузор и сопло, соответственно равны

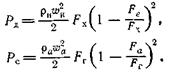
Согласно принятым выше условиям

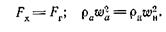
Тогда

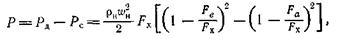
или

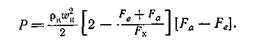
Рассмотрим двигатель с малыми скоростями в камере сгорания, т. е. с площадью камеры, существенно большей, чем площади входного и выходного отверстий:

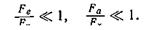
В этом случае мы приходим к следующей простой формуле для реактивной силы, определенной в результате вычитания силы, приложенной к соплу, из силы, приложенной к диффузору:

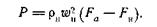
Тот же результат можно получить непосредственно из формулы для реактивной силы

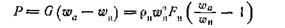
или, учитывая выведенное выше условие ,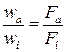

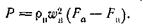
Итак, тяга получается за счет того, что сила давления на диффузор больше, чем на сопло. Это является следствием подогрева газа, в связи с которым площадь выходного отверстия приходится делать больше площади поперечного сечения набегающей струи.

В прямоточном воздушно-реактивном двигателе реактивная сила является результирующей сил давления, приложенных к стенкам внутреннего и наружного обводов двигателя.

Полезная часть реактивной силы, равная разности между реактивной силой и суммарным внешним сопротивлением двигательной установки, называется эффективной тягой:

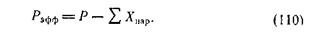
Реактивная сила двигателя, определяемая формулой (105), может рассматриваться как разность между выходным импульсом струи газов, рассчитанным по избыточному давлению на срезе сопла:

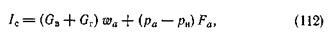
и входным импульсом струи набегающего невозмущенного потока воздуха, засасываемого в двигатель:

Оценку внутренней тяги двигателя (без учета внешнего сопротивления) производят с помощью относительного импульса (116)

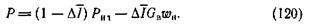
Величина

называется потерянным относительным импульсом сопла.

Дата добавления: 2014-01-11