Собственные числа и собственные векторы

Пусть дано векторное пространство Rⁿ.

Если существует правило (L), по которому любому вектору X Î Rⁿ ставится в соответствие единственный вектор YÎ Rⁿ, то такое правило называют оператором

или преобразованием в пространстве Rⁿ, причем вновь полученный вектор Y называют образом данного вектора Х, а данный вектор Х называют прообразом в новь полученного вектора Y.

Зададим квадратную матрицу n-го порядка А. И пусть преобразование состоит в том, что каждому вектору X Î Rⁿ ставится в соответствие вектор

7.1.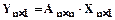

.

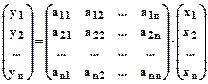Матрицу А, осуществляющую это преобразование называют матрицей оператора L.

Если оператор задан квадратной матрицей А, то он обладает двумя очень важными свойствами:

7.2. При сложении прообразов образы тоже складываются

.

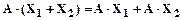7.3. Если прообраз умножить на скаляр, то образ тоже умножится на этот скаляр

.

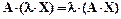Если оператор обладает свойствами 7.2. и 73., то его называют линейным оператором. Следовательно, квадратную матрицу n -го порядка А, столбцами которой являются базисные векторы пространства Rⁿ, можно рассматривать как матрицу линейного оператора. При этом переход к новому базису преобразует эту матрицу в матрицу 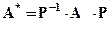, где Р - матрица перехода к новому базису, причем координаты новых базисных векторов в старом базисе образуют ее столбцы.

Векторному пространстве Rⁿ могут принадлежать такие векторы Х, для которых действие линейного оператора с матрицей А равносильно умножению на число.

7.4. Если для данного вектора Х и данного линейного оператора с матрицей А найдется такое число l, для которого выполняется условие 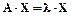, то такой вектор Х называют собственным вектором матрицы А, а число l - ее собственным числом.

Если дана матрица линейного оператора А, то все собственные числа этой матрицы можно найти из матричного уравнения 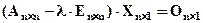. В этом уравнении Е - единичная матрица, О - нулевой вектор. Оно равносильно однородной системе линейных уравнений, которая имеет ненулевое решение только в том случае, когда определитель системы равен нулю: 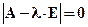. Это уравнение называют характеристическим уравнением матрицы (оператора).

Левая часть характеристического уравнения преобразуется в многочлен n -ой степени относительно неизвестного l. Такое уравнение имеет ровно n корней среди которых могут быть или не быть вещественные корни. Если окажется, что все корни вещественные различные, то матрица имеет n различных вещественных собственных чисел.

Если матрица линейного оператора - симметрическая, то все ее собственные числа являются вещественными числами, а собственные векторы, соответствующие любым двум собственным числам ортогональны.

Если в качестве базиса можно выбрать собственные векторы, то переход к этому базису приведет матрицу линейного преобразования к диагональному виду:

,

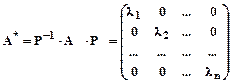где Р - матрица перехода к новому базису, столбцами которой являются собственные векторы, а l_i - их собственные числа.

Пример. Пусть линейный оператор задан матрицей .

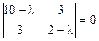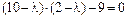Тогда характеристическое уравнение этой матрицы имеет вид: или или .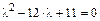

Корни этого уравнения 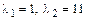и являются собственными числами данной матрицы.

Теперь найдем собственные векторы для каждого собственного числа.

Пусть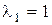, а собственный вектор для него 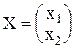, тогда 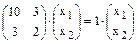или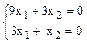

Определитель этой однородной системы отличен от нуля, следовательно она имеет бесчисленное множество решений, например: x₁=-u; x₂=3u, где u- параметр. Следовательно собственному числу 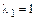соответствует бесчисленное множество собственных векторов вида .

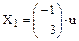Аналогичные вычисления приводят к определению собственных векторов для 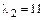из системы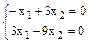

Получаем: x₁=3v, x₂=v, где v - параметр. Таким образом установили, что собственному числу 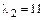соответствует бесчисленное множество собственных векторов вида .

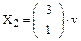Уравнение 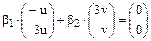имеет единственное (нулевое) решение, следовательно векторы X₁ и X₂ линейно независимы.

Скалярное произведение векторов 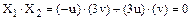, следовательно векторы X₁ и X₂ ортогональны и значит они образуют ортогональный базис пространства R².

Пусть собственные векторы X₁ и X₂ образуют теперь новый базис, тогда матрица перехода к новому базису будет иметь вид: 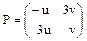. Обратная ей матрица 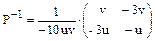и в новом базисе матрица линейного оператора будет иметь вид: .

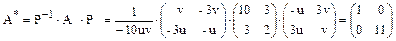Таким образом матрица линейного оператора приведена к диагональному виду, причем диагональными элементами являются ее собственные числа.

Дата добавления: 2014-01-11