Линейная модель обмена (модель международной торговли)

Модель Леонтьева (основная задача межотраслевого баланса)

ВЕКТОРЫ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ В ЭКОНОМИКЕ

Пусть в стране работает n отраслей народного хозяйства(n Î N): S₁, S₂,..., S_i,..., S_n.

Продукция каждой отрасли используется тремя способами:

- внутри самой отрасли,

- в других отраслях,

- как конечный продукт, направляемый на продажу внутри и вне страны.

Пусть известны также затраты отрасли S_i, потребные отрасли S_j для выпуска одной единицы своей продукции, и пусть они равны a_ij, (i = 1, 2,..., n; j = 1, 2,..., n). Это значит, что задана квадратная матрица n-го порядка (A_{n x n}), которую называют матрицей прямых затрат:

.

Основную задачу межотраслевого баланса (модель Леонтьева) можно сформулировать следующим образом.

Требуется определить необходимый объем выпуска продукции каждой отрасли так, чтобы обеспечить в каждой отрасли запланированный объем выпуска конечного продукта.

Если b_i - запланированный объем выпуска конечного продукта в отрасли S_i, то весь конечный продукт можно задать

вектором В_nx1, который называют вектором конечного продукта по отраслям: .

Пусть x_i - искомый объем выпуска отрасли S_i, тогда объем выпуска по отраслям можно задать вектором валового выпуска

по отраслям: .

В этих обозначениях задача имеет вид:

.

Уравнение называют моделью Леонтьева.

Ясно, что все матрицы в модели Леонтьева имеют только неотрицательные элементы.

Матричное уравнение (*) можно записать также в виде системы n линейных уравнений с n неизвестными. Матрица этой системы Q = E - A. Если матрица S - невырожденная, то система (*) имеет единственное решение:

.

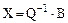Матрицу Q^-1 называют матрицей полных затрат. Каждый j -й столбец этой матрицы показывает затраты на производство единицы конечного продукта соответствующей отрасли.

Модель Леонтьева (*) и матрицу ее прямых затрат (А) называют продуктивными, если для любого вектора конечных продуктов найдется вектор необходимого выпуска продукции по отраслям .

Критерии продуктивности:

Пример.

Допустим, что имеются всего две отрасли народного хозяйства (n=2): энергетика и машиностроение. Энергетика запланировала валовый выпуск конечного продукта на сумму 144 млн рублей, а машиностроение - на сумму 123 млн рублей. Каждый млн. рублей валового выпуска конечной продукции энергетической отрасли требует 0,07 млн. рублей затрат валового выпуска своей отрасли и 0,12 млн. рублей затрат валового выпуска отрасли машиностроения. Каждый млн. рублей валового выпуска конечной продукции отрасли машиностроения требует 0,14 млн. рублей и 0,10 млн. рублей от энергетики и машиностроения. Требуется определить валовый выпуск продукции по отраслям, обеспечивающий запланированный валовый выпуск готового продукта. Из условий задачи следует, что вектор конечного продукта 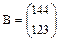, матрица прямых затрат , единичная матрица , искомый вектор валового выпуска по отраслям .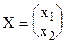

Критерии продуктивности выполняются, следовательно, для решения этой задачи можно использовать модель Леонтьева: .

В условиях решаемой задачи получим:

.

Ответ: При данной матрице прямых затрат валовый выпуск конечного продукта в энергетике в объеме 144 млн. рублей, а в машиностроении в объеме 123 млн. рублей можно обеспечить, если общий валовый выпуск в энергетике будет 179 млн. рублей, а в машиностроении - 160,5 млн. рублей

Рассмотрим n стран (n Î N): S₁, S₂,..., S_i,..., S_n с известным национальным доходом x₁, x₂,..., x_i,..., x_n соответственно.

Пусть a_ij - запланированная доля национального дохода страны S_j на покупку товаров у страны S_i, (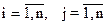). Числа a_ij можно записать в виде матрицы

.

В этой задаче квадратную матрицу А называют структурной матрицей торговли.

Будем считать, что весь национальный доход каждой страны S_i используется только на закупку товаров либо внутри самой страны (), либо на импорт из других стран (). Естественно, что в матрице А элементы неотрицательны и в каждом столбце сумма всех элементов равна единице.

Из перечисленных выше условий следует, что сбалансированная торговля возможна только при условии.

При получим систему линейных уравнений, которую в матричной форме можно записать как (*) ,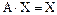

где А -структурная матрица торговли, а - вектор национальных доходов по странам.

Из уравнения следует, что вектор Х можно рассматривать, как собственный вектор матрицы А с собственным числом . Следовательно, только собственный вектор структурной матрицы торговли с собственным числом 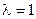даст национальные доходы стран, обеспечивающие сбалансированность торговли.

Пример. Дана структурная матрица торговли трех стран: .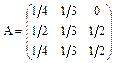

Определить, при каких национальных доходах этих стран торговля между ними будет сбалансированной.

Найдем собственный вектор матрица А при 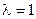. Для этого достаточно найти вектор Х из матричного уравнения . . .

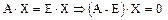После умножения всех уравнений на 12 расширенная матрица этой системы будет иметь вид: .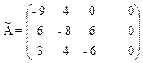

Метод полного исключения приводит к результатам:

.

Получили однородную систему двух линейных уравнений с тремя неизвестными. Однородная система всегда разрешима. Количество неизвестных равно 3, а ранг расширенной матрицы и матрицы системы равен 2, следовательно, система имеет бесчисленное множество решений, зависящих от оного параметра (3-2=1). Пусть x₁ =4t, тогда x₂ =9t, x₃ = 8t, где t - параметр. Это означает, что при данной структурной матрице торговля будет сбалансированной только при условии, что отношение национальных доходов этих стран будет равно 4: 9: 8.

Дата добавления: 2014-01-11