Примеры применения уравнения движения

ЛЕКЦИЯ 7

Применяя уравнения движения в интегральной форме, важно помнить, что контрольная поверхность S должна быть замкнутой. В качестве конкретного примера получим выражения для подъемной силы и сопротивления некоторого тела, обтекаемого жидкостью (рис. 4.2,а). Будем предполагать, что течение установившееся, жидкость идеальная, а массовые силы отсутствуют; тогда уравнение количества движения принимает такой вид:

(4.16) Проведем контрольную поверхность так, чтобы она была односвязной, могла быть

а)Рис.4.2

б)

стянута в точку и чтобы в нее вошла явным образом поверхность обтекаемого тела. Тогда поверхность S будет состоять из трех частей: S=S ₁+ S ₂+ S ₃ Здесь S ₁ – площадь контрольной поверхности произвольной формы, S ₂ – площадь поверхности тела, S ₃ – площадь поверхности щели или выреза, превращающего S в простую замкнутую поверхность (которую можно стянуть в точку).

Часть каждого из интегралов, определяемая площадью S ₃, равна нулю, так как и давления, и потоки количества движения с обеих сторон выреза уничтожают друг друга. Площадь S ₂ также не влияет на интеграл, определяющий поток коли-чества движения, так как нормальная к поверхности S ₂ составляющая скорости равна нулю (граничное условие – условие непротекания). Следовательно, уравнение (4.16) преобразуется к такой форме:.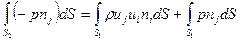

Интеграл, стоящий в левой части, определяет ту силу, с которой тело воздействует на поверхность жидкости S ₂. Поэтому, если изменить знак, то мы получим выражение для силы, действующей на тело со стороны жидкости:

. (4.17)

Если сопротивление X и подъемная сила Y определяются как составляющие силы P_j, направленные вдоль осей x ₁ и x ₂, получаем, что

,

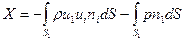(4.18)

.

Для определенности возьмем двумерное течение, для которого подынтегральные выражения преобразуются в соответствии с рис.4.2,б, а интегрирование ведется в направлении против часовой стрелки; при этом получим

, .

Форма контрольной поверхности S ₁ является произвольной; ее можно конкретизировать в виде прямоугольной «коробки», или кругового цилиндра, или в любом другом виде, удобном для расчета.

В качестве второго примера вычислим силу тяги ракетного двигателя (рис.4.3). Ракетный двигатель представим в виде цилиндрической камеры сгорания, к которой присоединен сужающе–расширяющийся канал, называемый соплом Лаваля. Под тягой будем понимать проекцию на ось двигателя результирующей силы давления газа, движущегося по проточной части, на стенки двигателя.

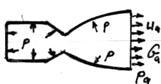Рис.4.3

Будем предполагать, что течение установившееся, массовые силы отсутствуют и газ идеальный; тогда уравнение количества движения будет иметь такой же вид, как и в первом примере:

На рис.4.3 можно видеть две составные части, из которых состоит контрольная поверхность S: S=S _дв +S _а.

Здесь S _дв - площадь внутренней поверхности двигателя, омываемой рабочим газом, S _а – площадь среза сопла, через которое вытекает одномерный поток идеального газа со скоростью u _а, давлением p _а и массовым расходом G _а.

Интеграл количества движения, определяемый по площади двигателя S _дв равен нулю вследствие непроницаемости стенок, поэтому уравнение движения преобразуется к такому виду: .

Интеграл в левой части уравнения определяет собой силу, с которой стенки двигателя воздействуют на поверхность газа, соприкасающегося со стенками. Следовательно, если изменить знак, то мы получим выражения для силы, с которой газ действует на стенки двигателя, т.е. силу тяги R:

(4.19)

Если двигатель покоится в атмосфере с давлением p_H, то формула для тяги примет вид:

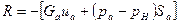. (4.19 а)

В том случае, когда давление газа на срезе сопла двигателя p _а равно атмосферному давлению p_H формула для вычисления тяги двигателя выглядит очень просто: .

Знак минус в формулах тяги говорит о том, что сила тяги – сила давления газа на стенки двигателя в проекции на ось двигателя, направлена против скорости истечения, противоположно направлению оси x.

Дата добавления: 2014-01-11