Разложение сигналов по различным базисам

Сравнение вариантов реализации изделия и определение лучшего из них.

Обобщенные оценки h_i определяются в соответствии с выражением (1). Для удобства вычислений составляется таблица 4, получившая название матрицы решений. В домашней задаче эта матрица имеет размерность 5 ´4. В верхнюю половину каждой клетки столбца матрицы записываются безразмерные оценки 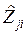вариантов из таблицы 3, а в нижнюю – результат умножения этой оценки на коэффициент значимости этого показателя, который был определен в табл. 2. Далее вычисляются суммы правых элементов матрицы в каждом столбце, которые и являются показателями степени совершенства h_i.

Табл. 4.

Показатели	Коэффи-циенты	Оценки качества вариантов системы
качества	значимости kj	I	II	III	IV
V	0,27	0,25 0,0675	0,33 0,0891	1,0 0,27	0,5 0,135
C	0,27	0,06 0,0162	0,125 0,0337	0,1 0,027	1,0 0,27
d	0,19	0,083 0,0157	0,05 0,095	1,0 0,19	0,125 0,0237
S	0,15	0,5 0,075	1,00 0,15	0,25 0,0375	0,33 0,0495
l	0,12	1,0 0,12	0,1 0,012	0,083 0,0099	0,125 0,015
Степень совер-шенства		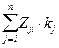0,2944	0,2943	0,5344	0,4932

Оценка степени совершенства вариантов показывает, что наиболее предпочтительным из них в заданных условиях применения является вариант 3.

Рекомендуемая литература.

1. Селезнева Н.В. Системный анализ. Конспект лекций. М.: МГАПИ, 2012.

Разложение периодических функций в тригонометрический ряд было известно еще Эйлеру и Бернулли (начало XVIII века). При этом считалось, что функция должна быть непрерывно гладкой, должны существовать и быть непрерывными ее производные. В 1822 году Фурье в поисках методов решения задачи теплопроводности пришел к выводу о возможности разложения в ряд по синусам и косинусам функции с периодом .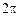

Заслугой Фурье было то, что он установил условия, которым должна удовлетворять разлагаемая в ряд функция. Функция может состоять из нескольких отрезков, аналитическое выражение которых различно; непрерывность функции необязательна, то есть она может иметь конечное число разрывов; необязательна и периодичность функции, поскольку это влияет на ее изображение только при выходе за пределы основного интервала разложения. Долгое время доказательства Фурье, который был физиком, считались математиками нестрогими. Его выводы получили строгое подтверждение лишь в XX веке после открытия интеграла Лебега. Однако его работы дали мощный толчок к развитию понятий о функции, сходимости рядов и введению понятия обобщенных рядов Фурье.

Прежде чем перейти к изложению вопроса об обобщенном ряде Фурье, рассмотрим несколько частных случаев разложения функции в ряд.

2.1 Ряд Фурье для сигнала с периодом Т

Функция с периодом Т может быть разложена в ряд по тригонометрическим функциям вида:

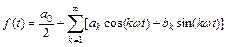, (1)

где

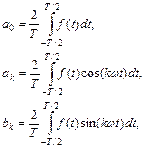(2)

для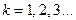

Коэффициенты разложения функции 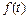в ряд (1), определяемые соотношениями (2), носят название коэффициентов Фурье.

Функция 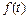должна быть непрерывной и несколько ее первых производных должны существовать и быть непрерывными.

Ряд Фурье можно записать и в иной, эквивалентной форме:

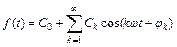, (3)

где

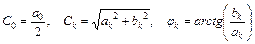. (4)

Таким образом, сложная функция 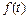может быть вполне определена совокупностью величин , где 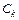– спектр амплитуд, 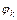– спектр фаз.

Для многих применений достаточно знать только спектр амплитуд сигнала; он применяется настолько часто, что под словом «спектр» обычно понимают спектр амплитуд. Графически принято изображать амплитуды отдельных гармоник вертикальными отрезками соответствующей длины (рисунок 1). Спектр периодической функции состоит из равноотстоящих спектральных линий (дискретный спектр); частоты гармоник находятся в простых кратных соотношениях. Амплитуды спектральных линий с увеличением номера k уменьшаются, вследствие сходимости ряда Фурье.

Рисунок 1 – Дискретный спектр периодической функции

2.2 Ряд Фурье для функции, заданной на отрезке конечной длины Т

Если функция времени f(t) задана только на отрезке конечной длины, то считать ее периодической нет оснований. Однако можно говорить о ряде Фурье для функции, получающейся периодическим продлением функции, заданной на отрезке конечной длины Т. При этом возможны два варианта:

1. – значения функции на концах интервала совпадают.

Рисунок 2 – Периодическое продление четной функции

При периодическом продлении такой функции никаких особенностей не возникает (рисунок 2), функция остается непрерывной (претерпевать разрыв будет только ее производная). Ряд Фурье вновь полученной функции аналогичен ряду Фурье (1), (2) для функции с периодом Т.

2. – значения функции на концах интервала не совпадают.

Продление такой функции с периодом Т приведет к появлению разрывов на концах интервала 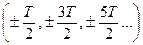(рисунок 3).

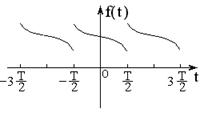
Рисунок 3 – Функция, имеющая точки разрыва

В точках разрыва ряд Фурье будет сходиться к величине , то есть будут наблюдаться нежелательные искажения (рисунок 4) – колебания, вызванные «явлением Гиббса». Чем меньше количество используемых гармоник в ряде Фурье, тем больше амплитуда пульсаций.

Рисунок 4 – Искажения в ряде Фурье для функции f(t)=t

Ланцош К. заметил, что пульсации усеченного ряда Фурье имеют период либо первой отброшенной, либо последней удержанной гармоники. Он доказал, что, сглаживая частичную сумму ряда путем интегрирования по этому периоду, можно устранить основные эффекты пульсаций. Сглаженный ряд Фурье представляет собой исходный ряд с коэффициентами, умноженными на сигма-факторы:

,

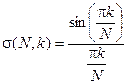где k – номер гармоники,

N – общее количество гармоник в ряде.

Дата добавления: 2014-01-11