Безусловный экстремум функционала

Простейшая задача вариационного исследования

Вариационное исследование – раздел математики решающий задачи определения наименьшего и наибольшего значений функционала, а так же определения наименьших и наибольших значений функционала, а также определения кривых, на которых достигается функционала.

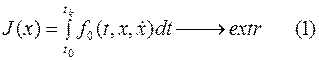
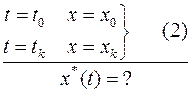
Частный случай функционала для одной переменной

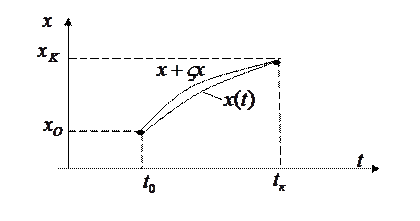
Искомые координаты заданы, с закрепленными концами. Функции гладкие. 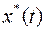- оптимальная кривая, доставляющая функционала (1)

Придадим этой кривой вариацию .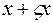

Отметим ограничения.

1. Кривые 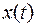и 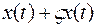должны быть близки по первому порядку.

2. 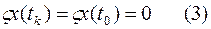т.е. вариации в граничных точках нулевые.

Запишем приращение функционала.

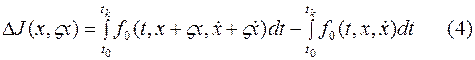
Возьмем подынтегральную функцию первого интеграла и разложим её в ряд Тейлора по вариациям 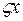и .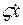

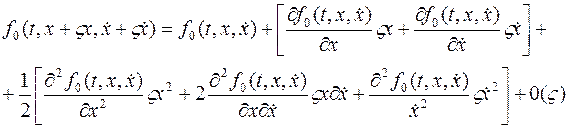
Подставим это выражение в (4), получим:

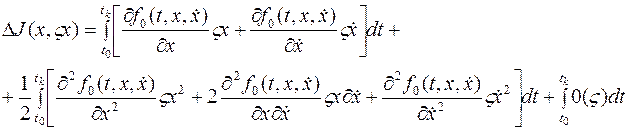
Первый интеграл в правой части этого выравнивания есть линейная часть приращения функционала, т.е. его первая вариация 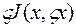, второй интеграл – это вторая вариация функционала 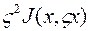, а третий интеграл получается из последующих членов разложения.

Мы раньше выяснили, что первым необходимым условием функционала является равенство нулю его первой вариации.

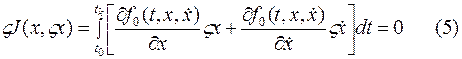
Для решения этого интегрального уравнения второе слагаемое подынтегрального выражения в правой части проинтегрируем по частям.

Обозначим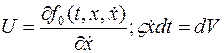

Поскольку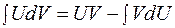

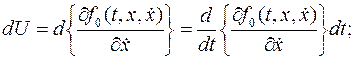
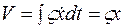, то

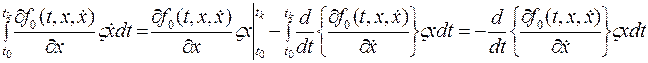поскольку первое слагаемое тождественно равно нулю в силу

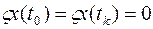
Следовательно, выражение (5) предстанет в виде:

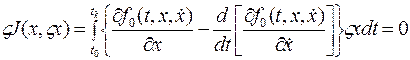
При произвольном 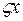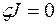, если будет равно нулю

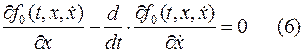
Это уравнение называется уравнение Эйлера решением которого является экстремаль 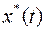, т.е. функция, доставляющая экстремум функционалу. Следует отметить, что уравнение Эйлера не всегда разрешимо, однако для многих важных практических случаев теории управления решение можно найти. Как нетрудно видеть, уравнение Эйлера представляет собой обыкновенное дифференциальное уравнение второго порядка. Общие решение такого уравнения содержит две произвольные постоянные, которые в общем случае могут быть определены с учетом граничных условий (2).

Для того чтобы определить 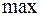или имеет функционал необходимо найти

(7) 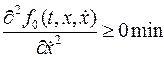, а если 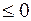то .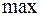

Это так называемое условие Лагранжа.

Пример.

Найти экстремаль 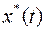, соответствующую функционалу

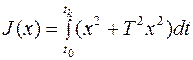при

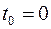
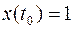
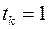
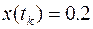
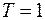
Поскольку 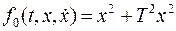, то уравнение (6) Эйлера для данной задачи имеет вид:

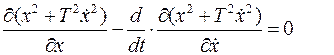или

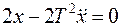, а при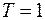

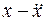=0. Этому дифференциалу уравнению соответствует характерное уравнение

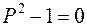с корнями .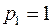

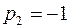Тогда общее решение дифференциального уравнения, т.е. поле экстремалей.

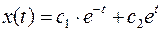
Заданным граничным условиям соответствуют нужные 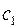и 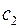и искомая экстремаль .

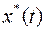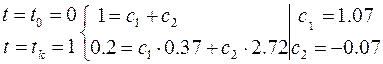
Откуда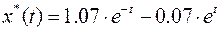

Условие Лежандра 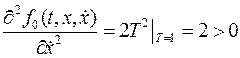т.е. имеет место минимум функционала.

В приложениях часто встречается задача с несобственным интегралом, например

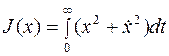
Уравнение экстремалей для него остается прежним

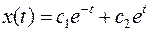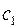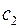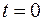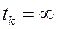, а постоянные интегрирования и определяются теперь из условий при и . При 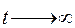движение должно быть устойчивым т.е. при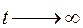 . Это может быть только в том случае, когда 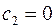. Следовательно, уравнение экстремали будет иметь вид 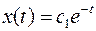. Постоянная 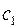определяется из начального условия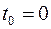 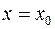; и искомая экстремаль будет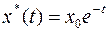

Рассматривая простейшую вариационную задачу, мы имеем дело с функционалом, экстремум которого зависит от скалярной функции 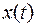. Получим необходимые условия экстремума функционала для общего случая.

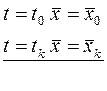
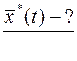
Данный функционал зависит от «n» функций 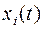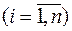. Здесь 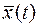-чисто математическая величина, которая с точки зрения физики явление может включать в себя и вектор состояния 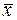и вектор управления 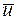функционала (2).

Получаем, что функция

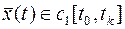и удовлетворяет граничным условиям

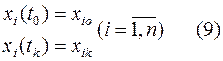
Подход решения такой:

1.Фиксируем все переменные кроме первой 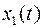. Затем проводим, т.е. же манипуляции и с другими переменными.

2. Фиксируем все переменные кроме второй. Получаем простейшую задачу относительно .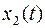

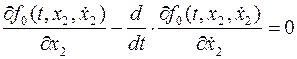
3. И т.д. до самой последней переменной

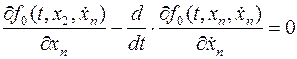
Решением уравнения будут экстремали

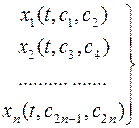Которые находим из граничных условий.

Для определения 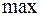или функционала, необходимо рассматреть условие:

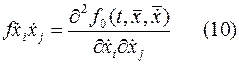
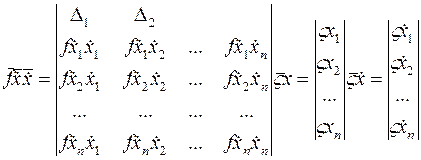
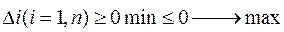
Простейшая вариационная задача легко обобщается на случай, когда подынтегральная функция содержит производные высших порядков и функционал имеет вид.

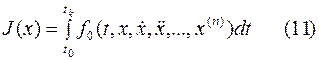
Экстремум определяется на класс кривых 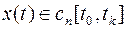, удовлетворяющих граничным условиям

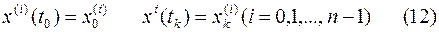
Методика получения первого необходимого условия экстремальной функции остается прежней: находится 1-ая вариация функционала и приравнивается нулю, что после ряда преобразований приводит к уравнению

,

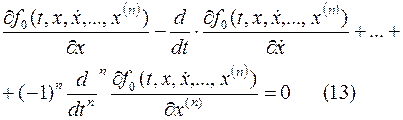которое называется уравнением Эйлера-Пуассона и представляет в общем случае нелинейное дифференциальное уравнение 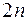-ого порядка. Его решение 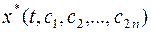. Содержит 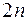постоянного интегрирования, которые находят на основании такого же количества заданных граничных условий.

Условие Лежандра в данной задаче следующие: для достижения минимума на некоторой экстремали необходимо выполнение неравенства

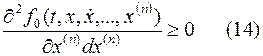, а для максимума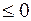

Пример.

Найти экстремаль функционала

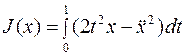
при граничных условиях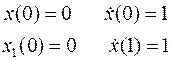

В рассматриваемом случае

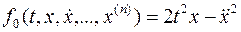, т.е.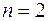

Уравнение Эйлера-Пуассона имеет вид

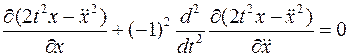
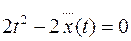, т.е.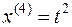

Отсюда:

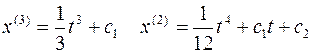
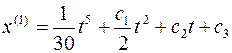
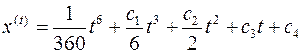
Найдем постоянные интегрирования.

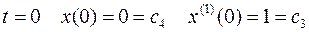
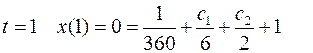
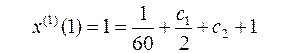
Отсюда ;

И экстремаль будет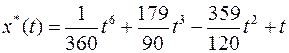

Условие Лежандра здесь

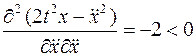и предполагает, что на данной экстремали достигается максимум.

Вариационные задачи на условный функционала

Задачи на условный экстремум функционала – это задачи вариационного исчисления, когда кривые 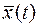, на которых задан функционал, помимо граничных условий должны удовлетворять некоторым другим условиям, например уравнениям связи или уравнениям объекта (1). Таким образом, пятая типовая задача управления есть частный случай задачи на условный функционала, правда в последней принято уравнение связи (1) представить с нулевой правой частью

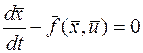или

вводя абстрактную математическую переменную 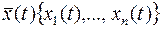, по физическому, включающую в себя и вектор состояния 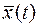и вектор управления 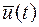, ограничения

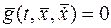или в скалярной форме

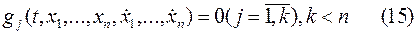
Тогда 5 типовая задача управления с абстрактной математической переменной 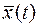будет выглядеть следующим образом:

Определить функционала

,

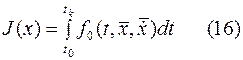при нем допустимые кривые 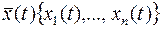удовлетворяют граничным условиям

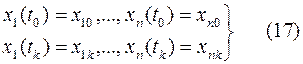
и условиям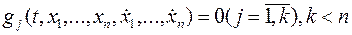

Уравнение связи (15) полагаются независимыми, т.е. ранг функций матрицы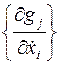

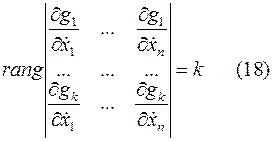
вдоль кривой доставляющей , для всех значений .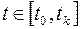

Таким образом, функционал (16) рассматривается не на всех допустимых кривых, удовлетворяющих граничным условиям (17), а только на тех кривых, которые удовлетворяют системе уравнений (15). Отметим, что граничные условия (17) и уравнения связи (15) должны быть согласованы, т.е. начальная и конечная точки должны принадлежать 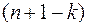мерному многообразию, которое задается системой равенств (15).

Изучая пятую типичную задачу, мы рассматриваем в качестве уравнений связи (15) дифференциальные уравнения. В общем случае в вариационной задаче на условный экстремум функционала в качестве уравнения связи могут быть использованы алгебраические

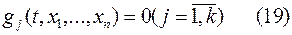
и интегрированные соответствия

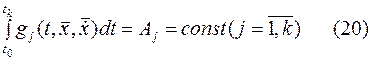
Если уравнения связи (15) являются дифференциалом (15), то имеет место общая задача Лагранжа. В случае (19) получается геодезическая задача или задача Лагранжа со сложными связями. Задачу при ограничениях, в форме интегральных соотношений (20) называют изотермической. Из всех 3-х более полной является общая задача Лагранжа, которую мы будем в дальнейшем рассматривать, а остальные могут быть получены, как частный случай задачи Лагранжа.

Общая задача Лагранжа решается аналогично задаче на условный функции с использованием метода неопределенных множителей Лагранжа, который мы изложим без доказательства.

Введем в рассмотрение новый функционал.

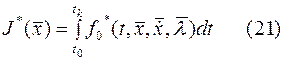, причем

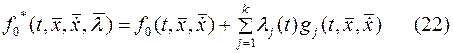
где 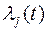- неопределенные пока (на момент постановки задачи) множители Лагранжа.

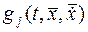- левые части уравнений связи (15) с нулевыми правами частями.

Подынтегральная функция (22) для геодезической задачи выглядит так

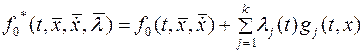, а для изопериметрической

,

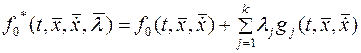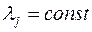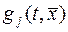причем , а и 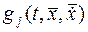в двух последних соотношениях берутся из выражения (19) и (20).

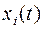
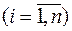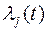
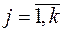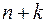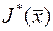Отметим, что в формуле (21) неизвестными являются и т.е. всего переменных. Найдем безусловный этого функционала по всем 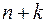переменным.

Для этого составим уравнения Эйлера-Лагранжа:

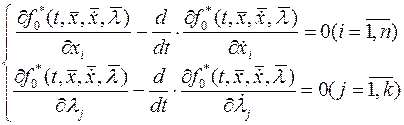
или с учетом (22) уравнение (6) примет вид

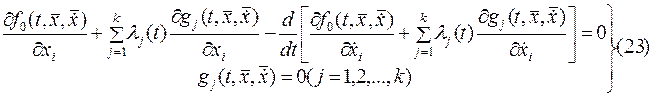
Эта система 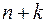уравнений содержит 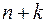неизвестных с 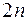произвольными постоянными, для определения которых используются граничные условия (17). Таким образом, система уравнений (23) позволяет найти неизвестные пока множители Лагранжа. 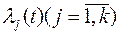и 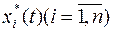, доставляющий безусловный функционала (21) и одновременно условный функционала (16) при наличии уравнений связи 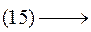или [(19) и (20) для геодезической изотермической задач].

Пример.

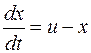уравнение связи объекта, инерционное звено

___________________

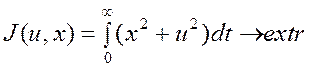
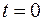
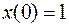
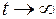
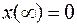
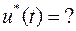
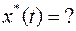
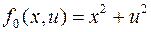
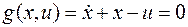
Конструируем вспомогательную функцию

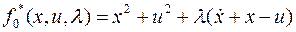
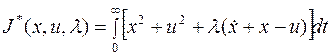
Уравнение Эйлера-Лагранжа для этого функционала.

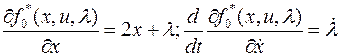
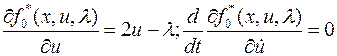
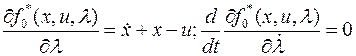
Тогда

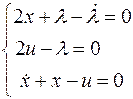
Отсюда следует

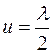
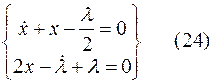
Отсюда характеристический определитель

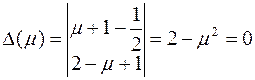
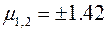
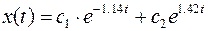
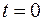
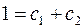
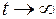
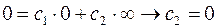
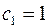
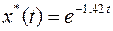
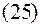подставим в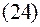

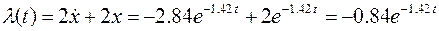
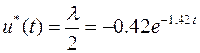
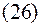
Результат решения задачи отображен на рисунка 1 и 2.

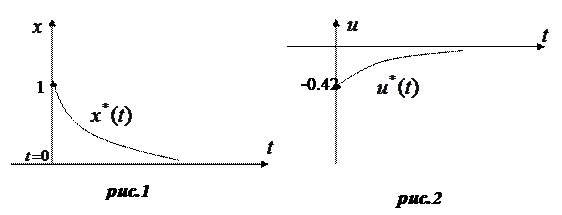
Найденное значение 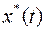и 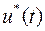позволяют осуществлять управление только по разомкнутому циклу

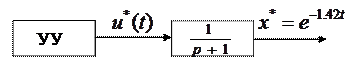
Алгоритм функционирования УУ можно получить и по замкнутому циклу.

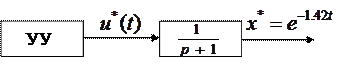
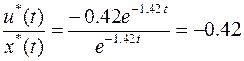
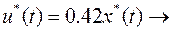регулятор

Если на и накладываются ограничения, то они становятся негладкими и решение будет сложным.

Глава III

Дата добавления: 2014-01-11