
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Принцип максимума для оптимальности по быстродействию
|
|
|
|
В этом случае минимизированный функционал имеет вид 
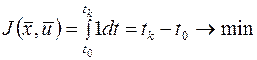 т.е. подынтегральная функция равна 1
т.е. подынтегральная функция равна 1
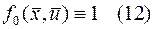
Запишем гамильтониан (9) с учетом (12)
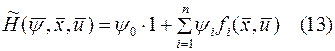
В отличие от общего случая будем теперь рассматривать 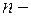 мерный вектор
мерный вектор
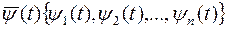
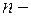 мерный гамильтониан
мерный гамильтониан
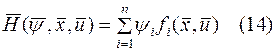 , тогда
, тогда
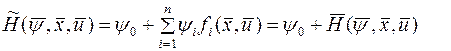
Тогда систему уравнений объекта (3) и сопряженную систему
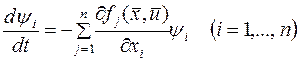
Запишем в виде
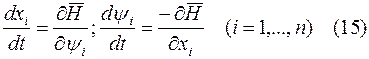 уравнения Гамильтона
уравнения Гамильтона
Обозначим
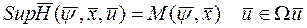
Если точная верхняя грань достигается, то
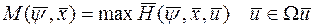
Очевидно, что для рассматриваемого случая
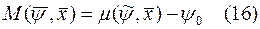 т.к.
т.к.
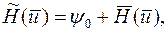 и
и 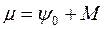
С учетом принятых обозначений основная теорема принципа максимума для оптимальности по быстродействию формируется следующим образом.
Пусть 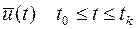 - некоторое допустимое управление, переводящее изображающую точку из состояния
- некоторое допустимое управление, переводящее изображающую точку из состояния  в состояние
в состояние 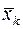 , а
, а 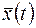 - соответствующая этому управлению траектория.
- соответствующая этому управлению траектория.
Для оптимальности по быстродействию управления 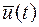 и траектории
и траектории 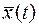 необходимо существование такой нулевой непрерывной вектор - функции
необходимо существование такой нулевой непрерывной вектор - функции 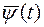 , удовлетворяющие системе уравнений (15), что
, удовлетворяющие системе уравнений (15), что
1) для всех 
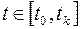 функция
функция 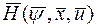 достигает по
достигает по 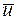 максимума
максимума
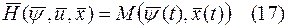
2) В конечный момент времени 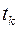 выполняется соотношение
выполняется соотношение
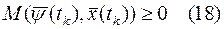
Как в общем случае, если функции 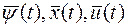 удовлетворяют (15) и условию (17), то функция
удовлетворяют (15) и условию (17), то функция 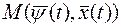 - постоянна. Поэтому проверку условия (18) можно производить с любой момент времени
- постоянна. Поэтому проверку условия (18) можно производить с любой момент времени 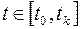 .
.
Замечание. т.к. для большинства случалось 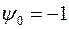 , то из (11) и (16) следует, что вдоль оптимальной траектории
, то из (11) и (16) следует, что вдоль оптимальной траектории
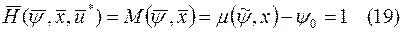

Для численных методов расчета оптимальных по быстродействию систем методом Понтрягина надо принимать для оптимального гамильтониана это значение.
Рассмотрим решение задачи на быстродействие аналитическим методом.
Пример.
Объект представляет собой два последовательно соединенных интегрирующих звена.
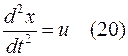
Требуется найти оптимальное управление 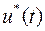 и уравнение регулятора
и уравнение регулятора 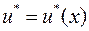 , чтобы система была оптимальной по быстродействию при переходе её из произвольного начального состояния в равновесное
, чтобы система была оптимальной по быстродействию при переходе её из произвольного начального состояния в равновесное 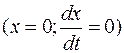 . При этом уравнение «
. При этом уравнение « » наложено ограничение
» наложено ограничение
|
|
|
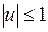
Решение.
Обозначив 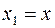 ,
, 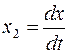 , приведем уравнение (20) к исходному виду
, приведем уравнение (20) к исходному виду
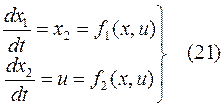
Тогда гамильтониан 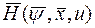 согласно (14) имеет вид
согласно (14) имеет вид
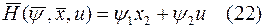
Согласно теореме Понтрягина надо найти 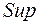 или
или 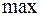 гамильтониана
гамильтониана 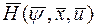 по управлению
по управлению  . Поскольку первое слагаемое (22) не зависит от
. Поскольку первое слагаемое (22) не зависит от  , то
, то 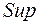 или
или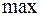
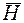 по управлению
по управлению  достигается одновременно с
достигается одновременно с 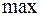 и
и 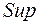 второго слагаемого
второго слагаемого 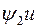 . Причем в силу линейной связи
. Причем в силу линейной связи 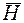 и
и 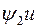
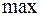 или
или 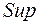
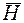 по
по  достигается при максимальном значении
достигается при максимальном значении 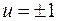 . Для того, чтобы согласно теореме Понтрягина
. Для того, чтобы согласно теореме Понтрягина 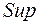 или
или 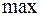
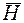
 т.е.
т.е. 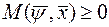 , знак у
, знак у  был бы одинаковым со знаком
был бы одинаковым со знаком 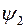 . Для определения
. Для определения 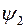 воспользуемся (15).
воспользуемся (15).
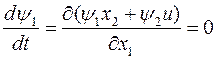 т.к.
т.к. 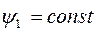
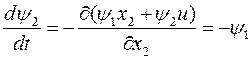 Откуда
Откуда
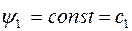
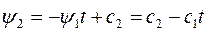
Отсюда, согласно ПМ для оптимальных по быстродействию систем
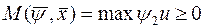 т.е.
т.е. 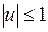
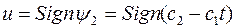 , т.е.
, т.е. 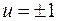 в зависимости от знака
в зависимости от знака 
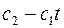 .
.
Поскольку линейная функция 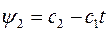 не более одного раза меняет знак, то в оптимальном процессе регулирования будет не более одного переключения с
не более одного раза меняет знак, то в оптимальном процессе регулирования будет не более одного переключения с 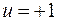 на
на 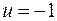 или наоборот, т.е. оптимальное управление
или наоборот, т.е. оптимальное управление 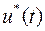 является не гладкой, а кусочно-постоянной функцией, у которой не более двух интервалов постоянства.
является не гладкой, а кусочно-постоянной функцией, у которой не более двух интервалов постоянства.
|
|
|
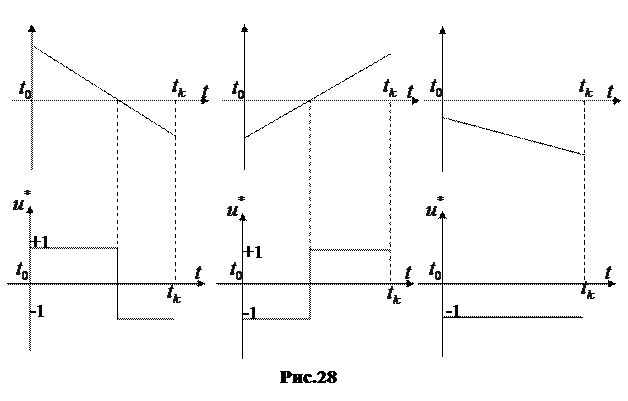
Следовательно, оптимальная по быстродействию система будут релейной, но необычной релейной, а особым специальным законом переключения реле по закону вспомогательной функции 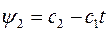 . Чтобы переставить всё это нагляднее, изобразим процесс на фазовой плоскости. Исключив из уравнения (21) время получим при
. Чтобы переставить всё это нагляднее, изобразим процесс на фазовой плоскости. Исключив из уравнения (21) время получим при 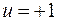 дифференциальное уравнение
дифференциальное уравнение 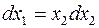 оттуда фазовая характеристика будет
оттуда фазовая характеристика будет
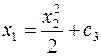 (23)
(23)
Аналогично при 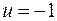 получаем
получаем
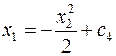 (24)
(24)
Это параболы симметричные относительно оси абсцисс  . Процесс должен заканчиваться в начале координат
. Процесс должен заканчиваться в начале координат 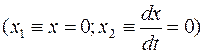 . Поэтому сначала изобразим фазовые траектории (параболы), вливающиеся в начало координат (т.е. при
. Поэтому сначала изобразим фазовые траектории (параболы), вливающиеся в начало координат (т.е. при 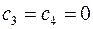 ) соответственно при
) соответственно при 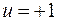 и при
и при 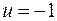 (изображение сплошными линиями и
(изображение сплошными линиями и 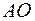 и
и 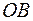 части парабол).
части парабол).
Нанесем теперь и все остальные параболы с различными значениями 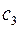 и
и 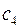 в формулах (23) и (24) до точек их вшивания в изображенные ранее две ветви парабол
в формулах (23) и (24) до точек их вшивания в изображенные ранее две ветви парабол 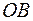 и
и 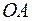 . Как видим из произвольной точки
. Как видим из произвольной точки 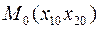 процесс идет по некоторой параболе
процесс идет по некоторой параболе  при управляющем сигнале
при управляющем сигнале 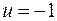 (в нижней области было бы
(в нижней области было бы 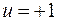 ). В точке
). В точке  происходит переключение на сигнал
происходит переключение на сигнал 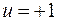 , после чего процесс идет по параболе
, после чего процесс идет по параболе 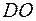 и заканчивается в точке «
и заканчивается в точке «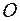 » за конечное время, которое согласно ПМ является минимальным из всех возможных для перехода данной системы из состояния
» за конечное время, которое согласно ПМ является минимальным из всех возможных для перехода данной системы из состояния 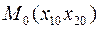 в равновесное состояние 0(0,0).
в равновесное состояние 0(0,0).
|
|
|
Точка переключения реле  может находиться в любом месте кривой
может находиться в любом месте кривой 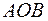 . последняя называется, поэтому Линней переключения. На ней лежат заключительные обрезки фазовых траекторий, проходящих в начало координат.
. последняя называется, поэтому Линней переключения. На ней лежат заключительные обрезки фазовых траекторий, проходящих в начало координат.
Итак, искомое уравнение преобразовательной части системы оптимальной по быстродействию будет
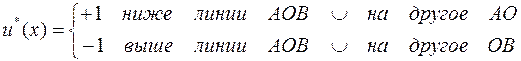
причем 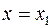 откладывается по оси абсцисс. Замечая, что
откладывается по оси абсцисс. Замечая, что 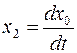 , из формул (23) и (24) для
, из формул (23) и (24) для 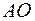 и
и 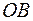 (т.е.
(т.е. 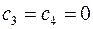 ) находим уравнение линии переключения
) находим уравнение линии переключения
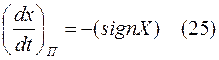
И, следовательно, уравнение преобразовательной части системы будет
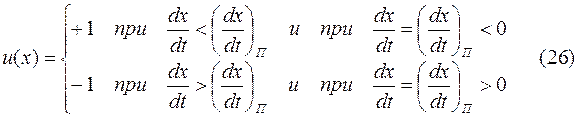
Тогда оптимальная по быстродействию САУ будет выглядеть следующим образом
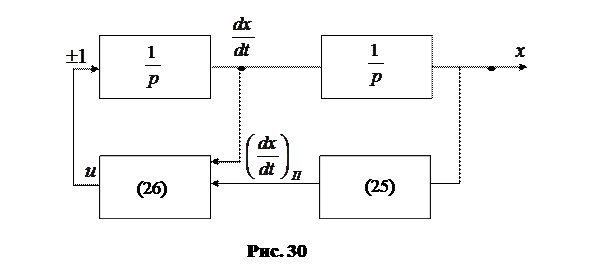 Т.о., в системе должны быть два измерения (для
Т.о., в системе должны быть два измерения (для  и для
и для 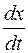 ). В управляющем устройстве должно автоматически вычисляться переключающее значение
). В управляющем устройстве должно автоматически вычисляться переключающее значение 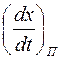 по формуле (25) и на основе сравнения фактического текущего значения
по формуле (25) и на основе сравнения фактического текущего значения 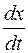 со значением
со значением 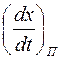 , зависящем от текущего
, зависящем от текущего  , должно производиться включение и выключение переключающего реле в соответствии с (26).
, должно производиться включение и выключение переключающего реле в соответствии с (26).
Это является специальным нелинейным законом управления для линейного объекта (20), приводящим к оптимальной по быстродействию системе. Таков результат простой 6 типовой задачи.
Решение по ПМ достаточно сложно даже для простейших случаев. Часто аналитическое решение не может быть получено, особенно при сложных ограничениях на  и
и  . В этом случае ищут приближенное решение кроме того, необходимо помнить, что ПМ дает только необходимое условие
. В этом случае ищут приближенное решение кроме того, необходимо помнить, что ПМ дает только необходимое условие  функционала. Отметим, что при численном расчете не исключен случай потери некоторых
функционала. Отметим, что при численном расчете не исключен случай потери некоторых  , в том числе и глобальных.
, в том числе и глобальных.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 369; Нарушение авторских прав?; Мы поможем в написании вашей работы!