Линии наибольшего наклона плоскости к плоскостям проекций

Прямая, лежащая в плоскости общего положения и перпендикулярная к линии уровня или следу плоскости, называется линией наибольшего наклона плоскости к соответствующей плоскости проекций.

Линии наибольшего наклона плоскости a к горизонтальной и фронтальной плоскостям проекций показаны на рис.3.9а и 3.9б, 3.10а и 3.10б.

Рис.3.9а Рис.3.9б Рис.3.10а Рис.3.10б

На рис.3.11приведен пример линии наибольшего наклона плоскости, заданной плоской фигурой - параллелограммом АВСD (линия m) - по отношению к горизонтальной плоскости проекций p₁. Построение ясно из чертежа.

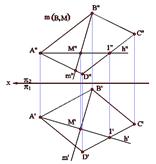
Рис.3.11

Поскольку линия наибольшего наклона перпендикулярна соответствующей линии уровня данной плоскости, то очевидно, что с помощью только одной линии - линии уровня плоскости по отношению к той или иной плоскости проекций, можно задать плоскость общего положения в пространстве. На рис.3.12 плоскость b задана линией наибольшего наклона к фронтальной плоскости проекций - линией n. Второй линией в этом случае является линия фронтали f, которую можно провести через любую точку линии l наибольшего наклона данной плоскости.

Рис. 3.12

Литература: Гордон В.О. и др. Курс н.г., 1988: с. 32-37; 42-49;62-64. Фролов С.А. Н.г., 1983.: с.34-42.

4. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ И ПЛОСКОСТЕЙ. ВЗАИМНАЯ ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ.

Из стереометрии известно: Если прямая параллельна какой-нибудь прямой, расположенной в плоскости, то она параллельна самой плоскости.

Пример 1 (рис.4.1). Найти горизонтальную проекцию прямой n, параллельной данной плоскости a (DАВС).

Рис.4.1

Решение:

Проведем в плоскости треугольника АВС прямую m”, параллельную n”, заданной прямой n.

Найдем ее горизонтальную проекцию m’ и параллельно ей через точку M’ проведем искомую прямую n’.

ВЗАИМНАЯ ПАРАЛЛЕЛЬНОСТЬ ДВУХ ПЛОСКОСТЕЙ

Из стереометрии известно: Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Пример 2 (рис.4.2). Через точку А провести плоскость b, параллельную плоскости a(аÇb).

Рис.4.2

Решение:

Проведем через точку А прямые с и d, соответственно параллельные прямые а и b заданной плоскости a, получим плоскость b(сÇd), параллельную заданной плоскости.

Две плоскости a(h₀aÇf₀a) и b(h₀bÇf₀b) будут параллельны между собой, если одноименные следы этих плоскостей будут попарно параллельны (рис.4.3).

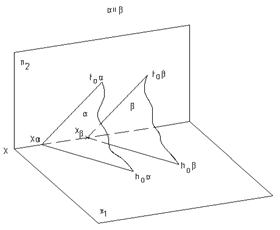
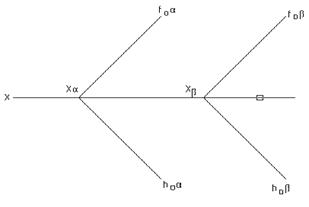
Рис.4.3а Рис.4.3б

ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ.

Задача на взаимное пересечение прямой и плоскости может быть сведена к одному из трех типов задач:

1. Обе геометрические фигуры проецирующего положения по отношению к плоскостям проекций (рис.4.4а и 4.4б).

Рис.4.4а Рис.4.4б

В этом случае искомый элемент - точка пересечения на чертеже уже есть, ее надо только выделить и обозначить.

2. Одна из заданных фигур проецирующего положения в пространстве, а другая - общего (рис.4.5а и 4.5б).

Рис.4.5а Рис.4.5б

В этом случае одна из проекций искомой точки пересечения на чертеже уже есть. Она принадлежит геометрической фигуре проецирующего положения, а другая ее проекция находится по принадлежности к фигуре непроецирующего положения.

3. Обе геометрические фигуры - линия и плоскость - общего положения в пространстве по отношению к плоскостям проекций.

В этом случае задача решается с помощью вспомогательной секущей плоскости в качестве “посредника”, которую проводят через заданную прямую.

На рис.4.6а и 4.6б приведены примеры пересечения прямой l с плоскостью треугольника АВС и прямой а с плоскостью b, заданной следами.

Рис.4.6а Рис.4.6б

ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ДВУХ ПЛОСКОСТЕЙ

Эта задача может также быть сведена к одной их трех типов задач, рассматриваемых выше в случае пересечения прямой с плоскостью.

1. Обе плоскости проецирующего положения по отношению одной или разным плоскостям проекций (рис.4.7а и 4.7б).

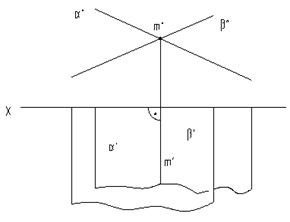
Рис.4.7а Рис.4.7б

В этом случае искомая линия пересечения плоскостей на чертеже уже есть. Ее нужно только выделить и обозначить.

2. Одна из плоскостей проецирующего положения, а другая - общего положения (рис.4.8а и 4.8б).

Рис.4.8а Рис.4.8б

3. Обе плоскости общего положения в пространстве.

В этом случае задача решается с помощью двух вспомогательных секущих плоскостей в качестве посредников. Такими посредниками будут проецирующие плоскости.

Пример 1 (рис.4.9). Найти линию пересечения двух плоскостей: a(а||b) и b(cÇd).

Рис.4.9

ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ, ЗАДАННЫХ СЛЕДАМИ.

Линия взаимного пересечения плоскостей, заданных следами, проходит через точки пересечения их одноименных следов. Решение задачи показано на рис.4.10а и 4.10б.

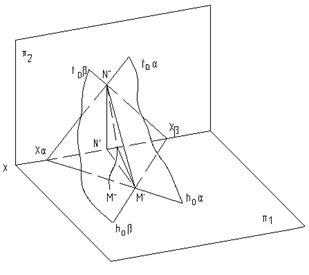
Рис.4.10а Рис.4.10б

Литература:

Фролов С.А. Начертательная геометрия. 2-е изд., изд.Машиностр. 1983., §§44;с.170.

Гордон В.О. и др. Курс начерт. геом., Глава IV до перпендикулярности.

Локтев В.О. Краткий курс начерт.геом. 1985. §§11, 12.

ИЗОБРАЖЕНИЕ МНОГОГРАННИКОВ

Многогранником называют тело, ограниченное плоскими многоугольниками. Многогранник, расположенный по одну сторону от плоскости его грани, называют выпуклым.

Грани, вершины и ребра многогранников связаны между собой соотношением, называемым теоремой Л.Эйлера: Г+В-Р=2, где: Г - число граней, В - число вершин и Р - число ребер.

Число граней многогранника не может быть меньше четырех, а сумма углов многоугольников, сходящихся в одной вершине, многогранных углов, не должно быть больше 2p.

Основные виды многогранников: пирамида, призма, правильные многогранники и многогранники, имеющие соответствующие одинаковые двугранные углы.

Многогранник представляет собой частный случай замкнутой многогранной поверхности.

ВИДЫ МНОГОГРАННИКОВ

Призмой называют многогранник, у которого две одинаковые взаимно параллельные грани - основания, а остальные грани - параллелограммы.

Пирамида представляет собой многогранник, у которого одна грань (произвольный многоугольник) принимается за основание, а остальные (боковые) грани - треугольники с общей вершиной.

Правильными называются такие многогранники, у которых все грани - правильные равные многоугольники. Так как в каждой вершине многогранника должны сходиться не меньше трех многоугольников, а у правильного многоугольника все углы равны, то величина угла многоугольника (грани) должна быть меньше 2p/3.

В правильном шестиугольнике углы равны 2p/3, поэтому в правильном многограннике грань не может быть шестиугольником.

Из сказанного можно сделать вывод, что правильных многогранников может быт только пять. В качестве граней правильных многогранников могут быть только правильный треугольник, четырехугольник и пятиугольник.

Правильными многогранниками являются: правильный четырехгранник или тетраэдр (грань - правильный треугольник), правильный шестигранник (куб) или гексаэдр (грань квадрат), правильный восьмигранник или октаэдр (грань правильный треугольник), правильный двенадцатигранник или додекаэдр (грань - правильный пятиугольник) и правильный двенадцатигранник или икосаэдр (грань - правильный треугольник).

Правильные многогранники называют Платоновы тела.

При изображении многогранника видимость его ребер и граней определяется с помощью конкурирующих точек.

ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ С ПОВЕРХНОСТЬЮ МНОГОГРАННИКА

Задача на пересечение прямой с поверхностью многогранника решается с помощью вспомогательной секущей проецирующей плоскости, проводимой через заданную прямую (рис.4.12).

Вспомогательная горизонтально проецирующая плоскость b(b`) проведена через прямую l.

Рис.4.12

ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКА ПЛОСКОСТЬЮ ОБЩЕГО ПОЛОЖЕНИЯ

Задача на пересечение многогранника плоскостью общего положения решается с помощью вспомогательных секущих плоскостей в качестве “посредников”. На рис.4.12а приведен пример пересечения трехгранной призмы DEFD₁E₁F₁ плоскостью треугольника АВС.

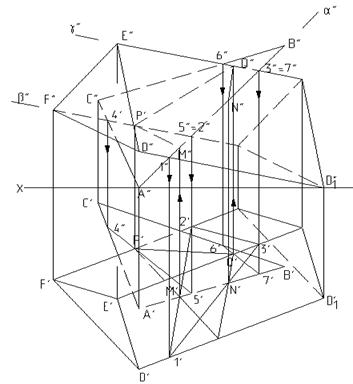
Рис.4.12а

Задача на рис.4.12а решена с помощью вспомогательных секущих плоскостей: a(a``), проведенной через сторону АВ треугольника АВС, которая пересекла призму по треугольнику 123, точки пересечения M и N c FD принадлежат искомой линии пересечения, и вспомогательных секущих плоскостей b(b`) и g(g``), с помощью которых найдены соответственно точки P и Q линии MPQN пересечения призмы DEFD₁E₁F₁ c треугольником АВС.

Определение видимости на чертеже не показано.

5. СПОСОБЫ ПРЕОБРАЗОВАНИЯ КОМПЛЕКСНОГО ЧЕРТЕЖА

Рассматривая способы решения главных позиционных задач, следует отметить, что задачи двух первых типов решаются значительно проще, чем задачи третьего типа.

В этой связи полезно отметить, что, зная способы преобразования комплексного чертежа, можно задачи третьего типа, при определенных условиях, преобразовать в задачи второго, которые решаются значительно проще.

Под преобразованием комплексного чертежа понимают всякое построение на чертеже, отражающее определенное построение в пространстве и приводящее к образованию новых полей проекций.

Принципиально имеют место два основных отличных друг от друга метода решения таких задач. С одной стороны, можно преобразовать чертеж путем введения новых плоскостей проекций, а, с другой стороны, упрощение может быть достигнуто за счет перемещения заданных фигур путем преобразования движения:

1) Плоскопараллельным перемещением заданных геометрических образов и 2) вращением их вокруг прямых частного положения в пространстве. Рассмотрим эти два метода.

5.1. СПОСОБ ВВЕДЕНИЯ НОВЫХ ПЛОСКОСТЕЙ ПРОЕКЦИЙ

1. Новая плоскость проекций должны быть перпендикулярной к одной из имеющихся плоскостей проекций. Любую, перпендикулярную к p₁ или p₂ плоскость, можно принять за новую плоскость проекций p₃ или p₄ (рис.5.1;5.2).

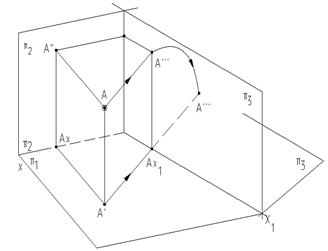
Рис.5.1 Рис.5.2

Этим способом можно решить четыре основные задачи на преобразование комплексного чертежа. Они следующие:

1. Задача на преобразование прямой общего положения в прямую уровня;

2. Задача на преобразование прямой общего положения в проецирующую прямую;

3. Задача на преобразование плоскости общего положения в проецирующую плоскость;

4. Задача на преобразование плоскости общего положения в плоскость уровня.

Рассмотрим эти задачи на примерах.

1. Преобразовать прямую l общего положения в прямую уровня и 2. Преобразовать прямую l общего положения в прямую проецирующую (рис.5.3).

Решение: Выберем на прямой l две точки А и В и введем новую плоскость проекций p₃, параллельную горизонтальной проекции этой прямой и перпендикулярно плоскости p₁, и спроецируем прямую l (А,В) ортогонально на эту плоскость. Получим новую проекцию l```(A```,B```). Первая основная задача решена.

Чтобы решить вторую основную задачу, продолжим построения дальше: Введем новую плоскость проекций p₄, перпендикулярную проекцию l```(A```,B```). Эта плоскость пересечет p₃ по оси х₂. Спроецируем на новую плоскость нашу прямую l в точку l^IV(A^IV,B^IV).

Вторая основная задача решена. Она, как промежуточное построение, содержит первую основную задачу.

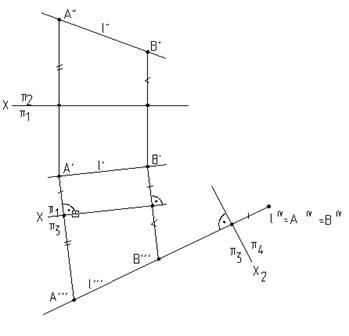
Рис.5.3

Рис.5.4

3. Преобразовать плоскость общего положения a(DАВС) в проецирующую плоскость;

4. Преобразовать плоскость общего положения a(DАВС) в плоскость уровня. (рис.5.4).

Решение: Проведем в плоскости треугольника АВС линию уровня, например, горизонталь h, и введем новую плоскость проекций p₃, перпендикулярную этой линии уровня, и спроецируем на нее треугольник АВС. Получим прямую B```C```A```, в которую он выродится. Третья основная задача решена.

5.2. ПОСТРОЕНИЕ ИЗОБРАЖЕНИЙ ФИГУР ПО ЗАДАННОМУ НАПРАВЛЕНИЮ

В машиностроительном черчении часто необходимо строить изображения заданных предметов или их частей по заданному направлению, указанному обычно стрелкой.

Пример 1. Построить изображение окружности по стрелке s.(рис.5.5).

Решение: Поскольку направление s параллельно фронтальной плоскости проекций, то новую плоскость проекций выбираем перпендикулярно направлению s`` и строим изображение этой фигуры на этой плоскости.

Рис.5.5

Пример 2. (рис.5.6). Построить изображение призмы по заданному направлению s общего положения в пространстве.

Решение: Перпендикулярно направлению s`` проводим ось проекций х₁, а перпендикулярно направлению s` - ось х₂.

Построение нового изображения призмы показано на чертеже и дальнейших пояснений не требует.

Рис.5.6

5.3. СПОСОБЫ ВРАЩЕНИЯ ВОКРУГ ПРЯМЫХ ЧАСТНОГО ПОЛОЖЕНИЯ

К способам вращения вокруг прямых частного положения относятся способы вращения вокруг проецирующих прямых и прямых уровня. Последний способ называется способом совмещения.

5.3.1. СПОСОБ ВРАЩЕНИЯ ВОКРУГ ПРОЕЦИРУЮЩИХ ПРЯМЫХ

Если некоторая точка А вращается вокруг проецирующей прямой i, то она будет перемещаться по окружности, плоскость которой перпендикулярна оси вращения, а, следовательно проецироваться эта окружность на плоскость проекций, перпендикулярную оси вращения, будет без искажения (рис.5.7, 5.8).

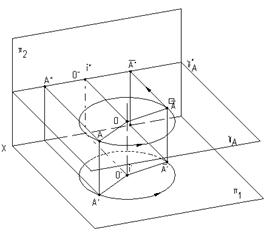
Рис.5.7

Рис.5.8

Для решения четырех основных задач на преобразование комплексного чертежа выбор осей вращения осуществляется из соображений упрощения процесса преобразования.

Покажем это на примерах решения четырех основных задач.

1-я и 2-я основные задачи решены на рис.5.9.

Чтобы преобразовать прямую l общего положения в прямую уровня, достаточно выбрать на прямой д две точки, например, А и В, а затем через одну из них провести ось вращения. Если, к примеру, необходимо преобразовать прямую l (А,В) во фронтальную прямую 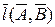, достаточно через одну из выбранных на этой линии точек провести горизонтально проецирующую прямую i, приняв ее за ось вращения, повернуть горизонтальную проекцию до положения , параллельно оси проекций. При этом на фронтальной плоскости проекций расстояние между точками А`` и В`` спроецируется в истинную величину. 1-я основная задача решена.

Для решения второй основной задачи продолжим построения и повернем нашу прямую 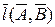вокруг оси j, перпендикулярной к фронтальной плоскости проекций и проходящей через точку А, до положения, перпендикулярного горизонтальной плоскости проекций. Получим проецирующую прямую . Вторая основная задача решена.

3-я и 4-я основные задачи решены на рис.5.10.

Для преобразования плоскости a(DАВС) в проецирующую плоскость достаточно провести в плоскости линию уровня, например горизонталь С-1, а затем выбрать ось вращения i, перпендикулярную горизонтальной плоскости проекций и проходящую через горизонталь С-1, а затем выбрать ось вращения i, перпендикулярную горизонтальной плоскости проекций и повернуть горизонтальную проекцию треугольника АВС до положения, при котором горизонталь С-1 станет фронтально проецирующей прямой. Тогда плоскость a(DАВС) станет фронтально проецирующей плоскостью.

3-я основная задача решена. для решения 4-й основной задачи достаточно продолжить построения и повернуть плоскость треугольника АВС вокруг проецирующей прямой j так, чтобы она расположилась параллельно горизонтальной плоскости, плоскости p₁. Четвертая задача на преобразование решена.

Рис.5.9

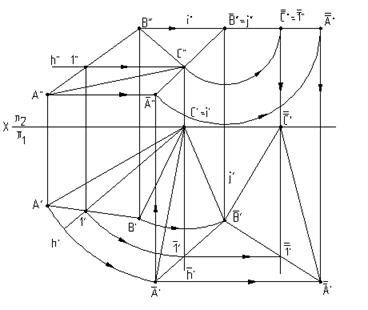
Рис.5.10

5.3.2. СПОСОБ ВРАЩЕНИЯ ВОКРУГ ЛИНИИ УРОВНЯ

Способ вращения вокруг линий уровня используется в начертательной геометрии главным образом для определения натуральных величин плоских фигур.

На рис.5.11 приведен пример определения натуральной величины треугольника АВС. Это решение равносильно решению четвертой основной задачи на преобразование комплексного чертежа и состоит в следующем:

Во-первых, в плоскости заданного треугольника проводится линия уровня, например, фронталь, вокруг которой нужно повернуть заданную фигуру до положения, параллельного фронтальной плоскости проекций, или совместить эту фигуру с плоскостью j, проходящей через выбранную линию уровня - фронталь f.

Во-вторых, поворот можно осуществить преобразовав заданную плоскую фигуру - треугольник АВС - в проецирующую плоскость, введя дополнительную плоскость проекций p₃, перпендикулярную фронтали f. Эта плоскость пересечет плоскость проекций p₂ по оси х₁. Проецируя треугольник АВС на эту плоскость, получим прямую А```C```B```. Аналогично решению на рис.5.10, плоскость треугольника A```C```B``` можно преобразовать в плоскость уровня относительно фронтальной плоскости проекций p₂, повернув вокруг фронтали f A```C```B``` до положения `````````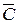. При этом горизонтальная проекция треугольника ``` 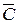совпадет с горизонтальной проекцией фронтали. Треугольник АВС спроецируется на p₂ в истинную величину. Плоскость треугольника совместилась с j``.

Но задача может быть решена без введения дополнительной плоскости проекций p₃, так как натуральную величину радиуса вращения точки В можно определить с помощью способа прямоугольного треугольника. Его применение показано на исходном чертеже и дополнительного пояснения не требует.

Рис.5.11

В случае задания плоскости ее следами, такую плоскость можно совместить с плоскостью проекций вращением вокруг соответствующего следа этой плоскости.

На рис.5.12 плоскость a(h_0aÇf_0a), заданная следами, совмещена с горизонтальной плоскостью проекций. Для нахождения совмещенного положения плоскости на ее фронтальном следе выбрана произвольная точка N(N``,N`) и из нее опущен перпендикуляр NO(N``O``,N`O`) на горизонтальный след плоскости. Дальнейшее построение аналогично решению задачи на рис.5.11.

При совмещении плоскости общего положения с плоскостью проекций может быть найдено совмещенное положение любой фигуры, принадлежащей этой плоскости, например, точки А.

На рис.5.13 плоскость b(h_0bÇf_0b) cовмещена с плоскостью p₂. Построения аналогичны и понятны из чертежа. При этом построении точка М(М``,M`) выбрана на горизонтальном следе плоскости, так как совмещение происходит путем вращения плоскости вокруг фронтального следа f_0b плоскости b.

Рис.5.12

Рис.5.13

Рис.5.14

На рис.5.14 приведен пример совмещения тупоугольной плоскости l с горизонтальной плоскостью проекций.

Совмещенное положение ` точки А, принадлежащей заданной плоскости, найдено с помощью вспомогательной прямой MN.

Литература:

Фролов С.А. Начертательная геометрия. М.: “Машиностроение”, 1983., гл.II, §§10,11,12.

Гордон В.О. и др. Курс начерт. геом. Изд. “Наука”, М.: Глава V, §§ 34, 37.

Локтев В.О. Краткий курс начерт.геом. М.: Гл.VII, §22.

5.4. CПОСОБ ПЛОСКОПАРАЛЛЕЛЬНОГО ПЕРЕМЕЩЕНИЯ

(Способ вращения без указания оси поворота)

Из планиметрии известно о преобразованиях “движение”, которые включают в себя ряд преобразований: параллельный перенос, вращение, преобразование симметрии и гомотетию. При этом одни преобразования могут быть заменены другими. Например, в случае параллельного переноса, а затем вращения отрезка, оба преобразования могут быть сведены к одному повороту, центр О вращения при этом может быть найден (рис.5.15, 5.16).

Рис.5.15(Параллельный перенос)

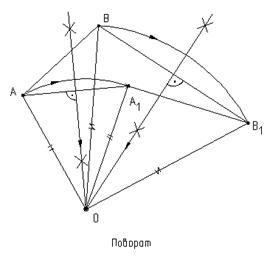
Рис.5.16 (Поворот)

Плоскопараллельный перенос фигуры в пространстве параллельно плоскости проекций, хотя и меняет положение фигуры, проекция этой фигуры на соответствующую плоскость проекций остается конгруэнтной.

Рассмотрим способ плоскопараллельного переноса на примере решения четырех основных задач на преобразование комплексного чертежа.

1-я и 2-я основные задачи (рис.5.17), 3-я и 4-я основные задачи (рис.5.18). Последовательность преобразования ясна из чертежей.

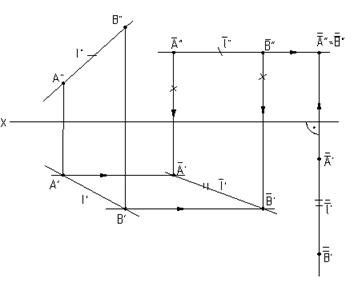
Рис.5.17

Рис.5.18

6. ВЗАИМНАЯ ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ

Теоретической предпосылкой для построения на комплексном чертеже проекций прямых и плоскостей, перпендикулярных по отношению друг к другу в пространстве, служит свойство проекции прямого угла, одна из сторон которого параллельна какой-либо плоскости проекции:

Если одна из сторон прямого угла параллельна плоскости проекции, то на данную плоскость прямой угол спроецируется прямым углом (рис.6.1, 6.2, 6.3).

Рис.6.1

Рис.6.2

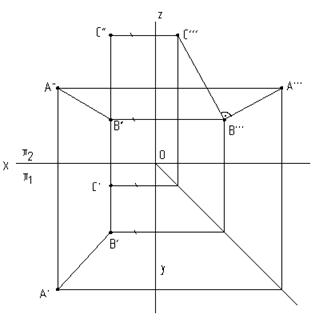
Рис.6.3

6.1. ВЗАИМНАЯ ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ

Для того чтобы прямая в пространстве была перпендикулярна плоскости, необходимо и достаточно, чтобы на эпюре горизонтальная проекция прямой была перпендикулярна к горизонтальной проекции горизонтальной плоскости, а фронтальная проекция - к фронтальной проекции фронтали этой плоскости (рис.6.4, 6.5).

Рис.6.4

Рис.6.5

6.2. ВЗАИМНАЯ ПЕРПЕНДИКУЛЯРНОСТЬ ДВУХ ПРЯМЫХ ОБЩЕГО ПОЛОЖЕНИЯ В ПРОСТРАНСТВЕ

Две прямые в пространстве будут взаимно перпендикулярными, если одна из них лежит в плоскости, перпендикулярной к другой прямой.

Пример (рис.6.6). Найти горизонтальную проекцию прямой а, проходящей через точку А и перпендикулярную к прямой b.

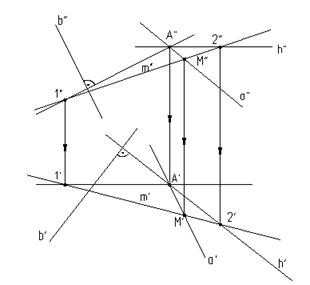
Рис.6.6

Решение: Проведем через точку А плоскость a(hÇf), перпендикулярную заданной прямой b, так как любая прямая, лежащая в этой плоскости, будет перпендикулярна прямой b.

С помощью вспомогательной прямой m найдем точку M`, принадлежащую искомой прямой а, и проведем проекцию а` этой прямой.

6.3. ВЗАИМНАЯ ПЕРПЕНДИКУЛЯРНОСТЬ ДВУХ ПЛОСКОСТЕЙ ОБЩЕГО ПОЛОЖЕНИЯ В ПРОСТРАНСТВЕ

Две плоскости в пространстве будут взаимно перпендикулярными, если одна из них содержит прямую, перпендикулярную к другой плоскости.

Пример (рис.6.7).

Через прямую l провести плоскость l, перпендикулярную к заданной плоскости b(hÇf).

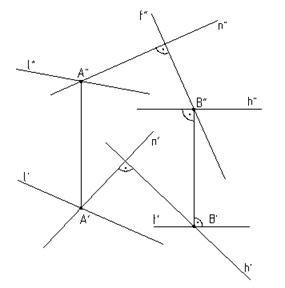
Рис.6.7

Решение: Через произвольную точку М на прямой l проведем прямую n, перпендикулярную к заданной плоскости b(hÇf).

Условие перпендикулярности согласно п.6.1.

Пересекающиеся прямые l и n и определят искомую плоскость l(nÇl).

7. МЕТРИЧЕСКИЕ ЗАДАЧИ И СПОСОБЫ ИХ РЕШЕНИЯ

Метрическими принято считать задачи, в условии или в решении которых присутствует численная характеристика.

К метрическим задачам относятся задачи на построение изображений фигур по их размерам или координатам из точек, измерение расстояний, углов, площадей и другие.

Метрические задачи бывают комплексными и включают в своем составе позиционные задачи.

Из всего многообразия метрических задач выделяют две задачи, которые называются основными метрическими задачами.

Первая задача - задача на перпендикулярность прямой линии и плоскости (п.6.1).

Вторая основная задача - задача на измерение расстояния между двумя точками способом прямоугольного треугольника.

Эти задачи называют основными потому, что на их основании можно решить любую другую метрическую задачу, то есть решение любой метрической задачи можно свести к решению основных метрических задач.

Кроме этого, метрические задачи можно решать и способами преобразования комплексного чертежа.

7.1. РЕШЕНИЕ МЕТРИЧЕСКИХ ЗАДАЧ В ОБЩЕМ ВИДЕ

Рассмотрим решение одной из метрических задач на примере, когда ее решение сводится к решению двух основных метрических задач.

Пример (рис.7.1).Измерить расстояние от точки А до плоскости a(hÇf).

Рис.7.1

Решение:

1.Опустим из точки А перпендикуляр на плоскость a(hÇf) и найдем его основание - точку К.

2.Способом прямоугольного треугольника измерим истинную величину отрезка АК.

Задача решена

|АК|=А₀K`.

7.2. РЕШЕНИЕ МЕТРИЧЕСКИХ ЗАДАЧ СПОСОБАМИ ПРЕОБРАЗОВАНИЯ КОМПЛЕКСНОГО ЧЕРТЕЖА

Способами преобразования комплексного чертежа могут быть решены только те метрические задачи, которые имеют только один геометрический элемент, несущий на себе одну искомую численную характеристику.

Алгоритм решения метрической задачи с помощью преобразования комплексного чертежа сводится к следующему:

1) определяется геометрический элемент оригинала, несущий на себе искомую численную характеристику и,

2) определяется “решающее положение” оригинала по отношению к плоскости проекций. (Решающим положением оригинала называют такое положение, при котором геометрический элемент, несущий на себе искомую численную характеристику, может быть спроецирован на плоскость проекций без искажений).

Решающих положений может быть только четыре и им соответствуют и четыре известных задачи на преобразование комплексного чертежа.

7.3. ИЗМЕРЕНИЕ РАССТОЯНИЙ

1.Расстояние от точки до прямой измеряется длиной перпендикуляра, опущенного из точки на данную прямую. Это расстояние будет проецироваться на плоскость проекций без искажения в двух случаях:

1)когда прямая перпендикулярна плоскости проекций, то есть когда решена вторая задача на преобразование;(рис.7.2);

2)когда прямая и точка расположены в плоскости, параллельной плоскости проекций, то есть когда решена четвертая основная задача. (рис.7.3).

2.Расстояние между двумя скрещивающимися прямыми будет проецироваться на плоскость чертежа без искажения, когда одна из прямых займет положение, перпендикулярное к одной из плоскостей проекций, то есть когда будет решена вторая основная задача на преобразование. (рис.7.4).

3.Расстояние между двумя параллельными прямыми спроецируется на плоскость проекций в истинную величину в двух случаях:1) когда прямые расположатся перпендикулярно плоскости проекций и, 2) будут лежать в плоскости, параллельной плоскости проекций, то есть когда будут решены соответственно вторая и четвертая основные задачи. (рис.7.5 и 7.6).

4.Расстояние от точки до плоскости проецируется на плоскость проекций без искажения, когда заданная плоскость будет проецирующей по отношению к плоскости проекций, то есть будет решена третья основная задача на преобразование чертежа. (рис.7.7).

Рис.7.2 Рис.7.3

Рис.7.4 Рис.7.5

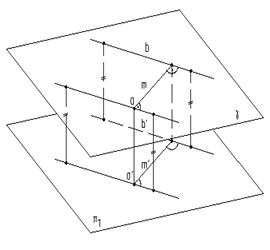
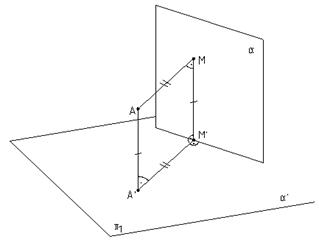
Рис.7.6 Рис.7.7

7.4. ИЗМЕРЕНИЕ УГЛОВ

1. Угол между двумя пересекающимися прямыми спроецируется на плоскость проекций в истинную величину, когда обе его стороны будут лежать в плоскости, параллельной плоскости проекций, то есть когда будет решена четвертая основная задача.

2. Угол между двумя плоскостями измеряется линейным углом двугранного угла, то есть тогда, когда линия пересечения плоскостей будет перпендикулярна плоскости проекций. Это возможно, если решена вторая основная задача на преобразование.

3. Угол между прямой и плоскостью измеряется углом между прямой и ее проекцией на плоскость, то есть когда плоскость этого угла расположится параллельно плоскости проекций, а это возможно в том случае, когда последовательными преобразованиями чертежа заданную плоскость сделать проецирующей, а прямую линию - линией уровня по отношению к этой плоскости проекций.

1. Плоский угол АВС=j⁰.

Рис.7.8

2. Двугранный угол j⁰ÐА01

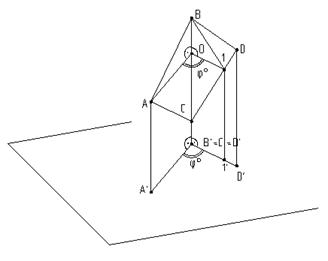
Рис.7.9

3. Угол между прямой АD и плоскостью АВС=j⁰.

Рис.7.10

8. КРИВЫЕ ЛИНИИ И КРИВЫЕ ПОВЕРХНОСТИ

8.1. КРИВЫЕ ЛИНИИ

Кривую линию можно рассматривать как след движущейся в пространстве точки или как совокупность точек, удовлетворяющих определенному уравнению. Кривая линия может являться результатом пересечения между собой кривых поверхностей или пересечения кривой поверхности плоскостью.

Если все точки кривой линии лежат в плоскости, то она является плоской, в противном случае - пространственной.

8.2. ПЛОСКИЕ КРИВЫЕ ЛИНИИ

Среди плоских кривых выделим, во-первых, кривые, называемыми алгебраическими. Такие кривые линии могут быть заданы алгебраическим уравнением. Степень уравнения определяет порядок кривой линии.

Линии первого порядка - прямые линии.

Кривые линии второго порядка - линии, алгебраическое уравнение которых - уравнение второй степени.

Линии второго порядка - это плоские кривые, определяемые: пятью точками, или четырьмя точками и одной касательной, или тремя точками и двумя касательными, или двумя точками и тремя касательными и т.д. Касательные могут проходить через задаваемые точки.

Линии второго порядка подразделяются на три вида: эллипс, гиперболу и параболу.

ЭЛЛИПС

Эллипс определяется уравнением х²/а² + y²/b² =1

Эллипс имеет две оси симметрии, следовательно и центр.

Наибольший диаметр эллипса - 2а называется большой осью, а малый диаметр - 2b - малой осью. Эти оси взаимно перпендикулярны.

Поскольку эллипс обладает многими геометрическими свойствами, существует множество способов построения его очерков

Рис.8.1

1.Сумма расстояний от любой точки эллипса до двух неподвижных точек, называемых фокусами, есть величина постоянная, равная 2а (рис.8.1).

М₁F₁+M₁F₂=2a

R₁+R₂=2a

AO=A₁O=a;F₁O=F₂O; где:

F₁O=e - ексцентриситет эллипса. ВF₁=BF₂=a.

Рис.8.2

2. С помощью двух концентрических окружностей. (рис.8.2).

Проводятся две концентрические окружности радиусами ОА и ОВ, а затем из центра О - произвольно выбранные лучи, пересекающие обе окружности в точках 1 и 2 соответственно.

С помощью лучей: 1₁-М₁ и 2₁-М₁ соответственно находят точки М₁ очерка эллипса.

3.по сопряженным диаметрам эллипса (рис.8.3).

Рис.8.3

Если заданы главные оси или два сопряженных диаметра эллипса, то есть такие диаметры, которые делят хорды, соответственно параллельные другому его диаметру пополам, то очерк эллипса можно построить по точкам, указанным на рис.8.3, способом

ГИПЕРБОЛА.

Гипербола определяется уравнением х²/а² - y²/b² =1

Рис.8.4

Гипербола обладает центром и двумя осями симметрии, имеет две несобственные точки.

Ось симметрии, называемая действительной, пересекает ветви кривой в вершинах А и А₁. Ось, перпендикулярная к действительной оси (и не пересекающую кривую), называют мнимой.

Прямые линии, проходящие через центр и определяющие несобственные точки М_¥ и N_¥, называются асимптотами.

При построении гиперболы желательно определить ее центр, диаметр АА и асимптоты.

Гипербола, как и эллипс, обладает многими свойствами, на основании которых можно найти множество точек этой кривой.

Гипербола - множество точек плоскости, разность расстояний (радиусов-векторов) которых до двух данных точек (фокусов) есть величина постоянная (равная 2а - действительной оси гиперболы)(рис.8.4).Множество точек гиперболы находят так:

Отмечают точки 1, 2, 3,... на действительной оси гиперболы, постепенно увеличивая расстояния между ними, и проводят из фокуса F₁ дуги радиусами, равными отрезкам А1, А2, А3,..., а из F₂ - отрезками А₁1, А₁2, А₁3,... Пересечение дуг А1 с А₁1, А2 с А₁2, А3 с А₁3,... - точки гиперболы: М₁, М₂, М₃,...

Для построения точек левой ветви кривой из точки F₂ проводят дуги радиусами А1, А2, А3,..., а из F₁ - радиусами А₁1, А₁2, А₁3,..., но можно использовать осевую или центральную симметрию, как это сделано на чертеже.

2. Построение гиперболы по ее осям, вершинам и точке М. (рис.8.5).

Рис.8.5

Проводят через точку М прямые линии, параллельные осям гиперболы и получают прямоугольник МРА₁Q, а затем диагональ PQ.

Из вершины А проводят произвольный луч, пересекающий МQ в точке 1₁, а из точки 1₁ - прямую, параллельную PQ, получая точку 2₁. Луч А₁2₁ пересечет луч А1 в точке М₁, принадлежащей гиперболе.

Аналогично находятся другие точки гиперболы.

Вторая ветвь гиперболы симметрично найденной.

ПАРАБОЛА.

Парабола определяется уравнением х²=2pz. (y²=2px).

Парабола имеет одну ось симметрии и одну несобственную на ней точку.

Рис.8.6

Парабола - множество точек плоскости, равноудаленных от точки (фокуса) и прямой (директрисы), лежащих в плоскости.

Величина р - расстояние между фокусом и директрисой - параметр параболы. На этом свойстве основано построение параболы по заданным фокусу и директрисе (рис.8.6).

Парабола может быть построена по ее оси, вершине А и точке М одним из двух способов (рис.8.7). Построение точек указано стрелками.

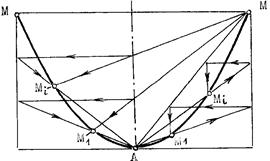
Рис.8.7

Все диаметры параболы параллельны ее оси, так как центр параболы - несобственная точка. Хорды параболы, которые делятся одним из диаметров пополам, называются сопряженными с этим диаметром.

Касательная в конце такого диаметра параллельна сопряженным с ним хордам. (рис.8.8).

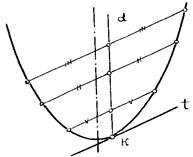
Рис.8.8 Рис.8.9

Простой способ проведения касательной к параболе в данной точке дан на рис. 8.9.

ТРАНСЦЕНДЕНТНЫЕ КРИВЫЕ.

Трансцендентными называют кривые линии, заданные, неалгебраическими уравнениями. Например, синусоида. Ее уравнение у=sinx, характеризуют изменение синуса угла в зависимости от величины угла, или циклоида, параметрическое уравнение которой имеет вид: х=r(t - sint), y=r(1+сost).

Более подробно построение кривых линий описано в учебниках по машиностроительному черчению.

Литература.

Левицкий В.С. Машиностроительного черчение: Учебник для студ. втузов - М.:Высш.шк., 1988.

8.3. ПРОСТРАНСТВЕННЫЕ КРИВЫЕ

Пространственные кривые линии - это, главным образом, линии пересечения кривых поверхностей. Так, например, две поверхности второго порядка пересекаются по линии четвертого порядка, представляющей собой пространственную кривую.

8.4. ПРОЕЦИРОВАНИЕ КРИВЫХ ЛИНИЙ

Кривая линия в общем случае проецируется кривой линией (рис.8.10).

Рис.8.10

Алгебраические кривые проецируются кривыми линиями того же порядка, что и сами кривые.

Кривые второго порядка проецируются кривыми линиями второго порядка.

При параллельном проецировании эллипс и окружность проецируются в эллипс или, в частном случае, в окружность; проекция параболы - парабола, проекция гиперболы - гипербола.

При проецировании окружности любая пара ее взаимно перпендикулярных диаметров проецируется парой сопряженных диаметров эллипса.

8.5. ОСОБЫЕ ТОЧКИ КРИВОЙ ЛИНИИ

Прямая, пересекающая кривую линию в двух и более точках, называется секущей. Если эти точки оказываются бесконечно близкими (совпадают), прямую, проходящую через эти точки, называют касательной к кривой. На рис.8.11 показано, как секущая l, вращаясь вокруг точки К, превращается в касательную t.

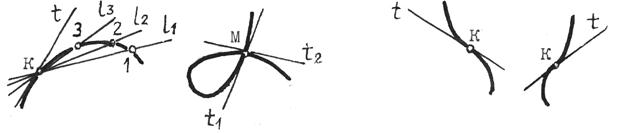
Рис.8.11 Рис.8.12 Рис.8.13.

К особым точкам кривых линий относят:

1. Точки самопересечения линий (рис.8.12). В этих точках к кривой можно провести две и более касательных.

2. Точки перегиба кривой - точки, которые разделяют участки, кривизна которых имеет различное направление (рис.8.13).

3. Точки возврата - точки, в которых кривая имеет только одну касательную и относительно которой ветви кривой располагаются по одну сторону.

4. Экстремальные точки - точки, наиболее близкие или наиболее удаленные от наблюдателя или от плоскости проекций.

8.6. СПОСОБЫ ОБРАЗОВАНИЯ И ЗАДАНИЯ КРИВЫХ ПОВЕРХНОСТЕЙ

Кривая поверхность может рассматриваться как совокупность всех положений некоторой линии, движущейся в пространстве. Движущуюся линию в этом случае называют образующей поверхности, а линии (иногда и точки), определяющие закон ее перемещения, - направляющими.

Совокупность точек, линий и различных условий, определяющих закон перемещения образующей, называют также определителем поверхности.

8.7. ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ

Поверхность, образуемая движением прямой линии, называется линейчатой. На рис. 8.14 линейчатая поверхность образована движением прямой образующей l, постоянно проходящей через точку s и во всех своих положениях пересекающей некоторую направляющую m. Эта поверхность называется конической. На рис.8.15 линейчатая поверхность образована движением образующей l, перемещающейся параллельно самой себе и пересекающей направляющую кривую n. Такая поверхность называется цилиндрической. На рис.8.16 поверхность образуется движением прямой линии, пересекающей две кривые направляющие линии а и b, и параллельной плоскости параллелизма l. Такая поверхность называется цилиндроидом. При этом направляющие линии могут быть как плоскими, так и пространственными.

Рис.8.14 Рис.8.15 Рис.8.16

Если одна из направляющих поверхности с плоскостью параллелизма - прямая линия, то поверхность называют коноидом, если обе направляющие - прямые линии, то - косой плоскостью или гиперболическим параболоидом.

8.8. ПОВЕРХНОСТИ ВРАЩЕНИЯ

На рис.8.17 поверхность образована вращением образующей l вокруг оси i. При этом точки образующей перемещаются по окружностям, плоскости которых перпендикулярны к оси вращения.

Через любую точку на поверхности вращения можно провести только одну параллель и один меридиан. Наибольшую параллель называют экватором, а меридиан, параллельный плоскости проекций, - главным меридианом.

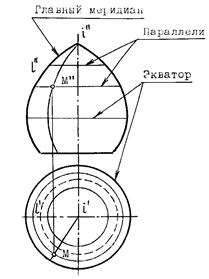
Рис.8.17 Рис.8.18

8.9. ПОВЕРХНОСТИ, ЗАДАВАЕМЫЕ КАРКАСОМ

На рис.8.18 топографическая поверхность задана горизонталями. Любую точку на такой поверхности можно задать с помощью линии на этой поверхности, проходящей через эту точку. На рисунке точка М поверхности лежит на линии, пересекающей горизонтали этой поверхности.

В авиационной промышленности, в судостроении и автомобилестроении теоретическая поверхность изделия задается плоскими сечениями, параллельными горизонтальной, фронтальной, профильной плоскостям проекций. На рис.8.19 изображен фрагмент такой поверхности. Плоские сечения теоретического каркаса горизонтальными плоскостями называют горизонталями, фронтальными плоскостями - батоксами, а профильными - шпангоутами.

Если поверхность на чертеже задана своим определителем, то на ней можно построить сколь угодно плотный каркас. Например, на поверхности вращения - каркас параллелей, а на поверхности конуса - каркас его образующих

Рис.8.19

Фрагмент теоретического чертежа корпуса мини-яхты “Дюгонь”.

Проекции: полуширота и бок (шпангоуты, батоксы, высоты от КВЛ (рис.8.20).

Рис.8.20

На рис.8.21 изображен фрагмент задания на чертеже фюзеляжа модели самолета-истребителя ЛА-11, заданного набором поперечных сечений (М1:50). Журнал “Моделист-Конструктор” №5, 1973 г.

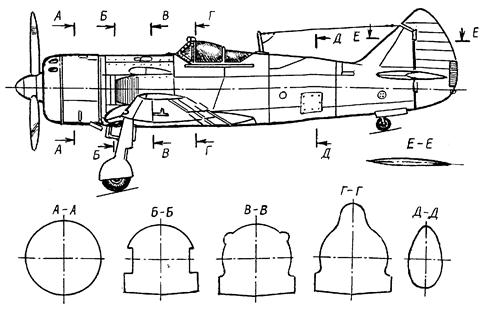
Рис.8.21

8.10. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА

Поверхности, выражаемые алгебраическим уравнением второй степени, называют поверхностями второго порядка. Порядок алгебраической поверхности равен степени ее уравнения. Поверхность, определяемая алгебраическим уравнением первой степени, есть плоскость. Среди поверхностей второго порядка выделим:

1.Эллипсоиды. Они имеют каноническое уравнение следующего вида х²/а² + y²/b² + z²/c²=1. Эллипсоиды подразделяются на трехосные (а¹b¹с¹а, рис.8.22), вращения (а=b¹с¹а, рис.8.23) или (а¹b=с, или а=с¹b) и сферу (а=b=c).

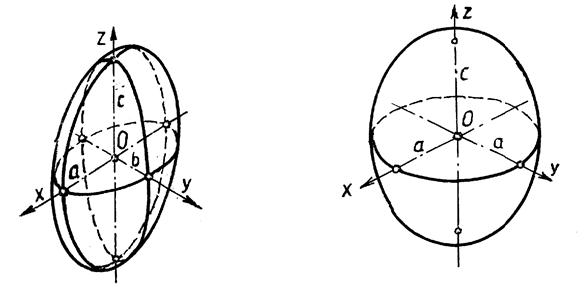
Рис.8.22 Рис.8.23

2. Параболоиды. Параболоиды эллиптические (рис.8.25) имеют уравнение х²/р + y²/b=2z. Параболоид вращения имеет уравнение z²=2px.

3. Параболоиды гиперболические (рис.8.26) имеют уравнение вида: х²/р-y²/q=2z и являются линейчатыми поверхностями (косая плоскость).

Рис.8.24 Рис.8.25

Гиперболоиды.

а) Гиперболоиды однополостные (рис.8.26) имеют уравнение вида: х²/а²+y²/b²-z²/c²=1 и являются линейчатыми поверхностями.

б) Гиперболоиды двухполостные (рис.8.27) имеют уравнение вида х²/а²+y²/b²-z²/c²=-1.

Гиперболоиды могут быть поверхностями вращения.

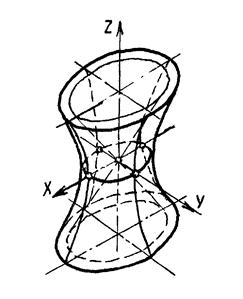
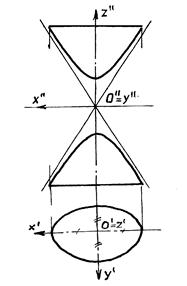
Рис.8.26 Рис.8.27

Поверхности второго порядка могут быть подобными.

Два эллипсоида подобны, если отношение их полуосей одинаково: а:b:c=a₁:b₁:c₁.

Два эллиптических параболоида подобны, если подобны их сечения плоскостью, перпендикулярной к оси.

Два гиперболических параболоида подобны, если их асимптотические плоскости составляют одинаковые углы.

Два гиперболоида подобны, если они имеют одинаковые асимптотические конические поверхности.

8.11. НЕКОТОРЫЕ СВОЙСТВА ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА

1. Прямая пересекает поверхность в двух точках: действительных, совпадающих или мнимых.

2. Поверхность пересекается плоскостью по кривой второго порядка, которая может распадаться на две прямые (пересекающиеся, параллельные или совпавшие).

3. Через два сечения поверхности второго порядка можно провести конус или цилиндр (задача имеет два решения).

4. Поверхность может быть задана двумя кривыми второго порядка и точкой, или касательной плоскостью. При этом на положение кривых накладывается такое ограничение: обе кривые должны принадлежать одной конической (цилиндрической) поверхности. Такие кривые называются гологичными.

5. Три кривые второго порядка, принадлежащие трем плоскостям попарно пересекающиеся в шести точках, определяют единственную поверхность второго порядка. Если одна из кривых распадается на две прямые, то поверхность будет линейчатой.

6. К центральным поверхностям второго порядка относятся: эллипсоид, однополостный и двуполостный гиперболоиды. Отрезок прямой, проведенный через центр и соединяющий две точки пересечения с поверхностью, называется диаметром. Центр поверхности делит этот отрезок пополам.

7. Поверхность может быть задана девятью произвольными точками. Чтобы написать уравнение такой поверхности, необходимо подставить в уравнение поверхности координаты заданных точек и решив систему девяти линейных уравнений, получить значения коэффициентов.

8. Эллипсоид, двуполостной гиперболоид и эллиптический параболоид относятся к нелинейчатым поверхностям. Все остальные - линейчатые.

Все эти свойства поверхностей второго порядка могут быть обнаружены методом сечений данных поверхностей плоскостями

При каноническом (нормальном) задании поверхностей исследование легко проводится с помощью проецирующих плоскостей.

Метод плоских сечений является основным методом исследования и задания поверхностей сложной формы в технике.

8.12. СЕЧЕНИЕ ПОВЕРХНОСТИ ПРОЕЦИРУЮЩЕЙ ПЛОСКОСТЬЮ И ПРЯМОЙ ЛИНИЕЙ

Чтобы построить сечение поверхности какой-либо проецирующей плоскостью, необходимо сначала построить каркас линий, принадлежащей этой поверхности. Каркас поверхности может быть образован дискретным множеством линий, образующих данную поверхность. Примером таких линий могут быть параллели на поверхности вращения, образующие линейчатой поверхности и тому подобное.

Секущая плоскость, в данном случае проецирующая, пересечет линии каркаса в соответствующих точках, соединяя которые в определенной последовательности от одной линии каркаса к другой, следуя их расположению на каркасе, можно получить фигуру сечения поверхности заданной секущей плоскостью.

Покажем это на примерах.

Пример 1 (рис.8.30). Построить сечение цилиндра горизонтально проецирующей плоскостью b(b`).

Решение:

1.Строим каркас образующих на поверхности заданного цилиндра - линии:l, l₁, l₂, l₃,...

2. Заданная плоскость пересечет их соответственно в точках: 1, 2, 3,..., соединяя которые получим искомую линию пересечения.

Подобные задачи решаются на комплексных чертежах аналогично этому примеру

Рис.8.30

Пример 2 (рис.8.31). Построить линию сечения поверхности вращения фронтально проецирующей плоскостью a(a`).

Решение понятно из чертежа.

Рис.8.31

КОНИЧЕСКИЕ СЕЧЕНИЯ

К коническим сечениям относятся кривые линии и частные случаи таких линий, получающиеся при пересечении конуса второго порядка плоскостью. К этим линиям относятся: эллипс (в частном случае окружность), гипербола (в частном случае две пересекающиеся прямые) и парабола (в частном случае две совпавшие прямые линии)(рис.8.32, 8.33, 8.34).

Эллипс (плоскость a пересекает все образующие конуса).

Парабола (плоскость a параллельна только одной образующей конуса).

Гипербола (плоскость a параллельна двум образующим конуса SL₁ и SL₂).

Рис.8.32 Рис.8.33

Рис.8.34

ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С КРИВОЙ ПОВЕРХНОСТЬЮ

При построении точек пересечения прямой линии с кривой поверхностью вспомогательную секущую плоскость стараются выбрать таким образом, чтобы она пересекла кривую поверхность по линии, легко определяемой на чертеже, то есть по инструментально простой линии: прямой или окружности.

Алгоритм решения:

1. Заданную прямую заключают во вспомогательную секущую плоскость (чаще проецирующую);

2. Строят сечение заданной поверхности этой плоскостью;

3. Находят общие точки фигуры сечения с заданной прямой;

4. Определяют видимость прямой линии относительно поверхности. В этом случае можно воспользоваться конкурирующими точками.

Пример 1 (рис.8.35). Найти точки пересечения прямой l с поверхностью конуса.

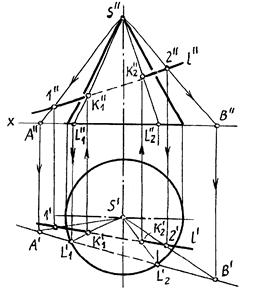
Рис.8.35

На рис.8.35 вспомогательная секущая плоскость проведена через прямую l и вершину S конуса. Она пересекла конус по образующим SL₁ и SL₂.

Вспомогательная секущая плоскость задана прямыми S1 и S2, а ее горизонтальный след - линия АВ.

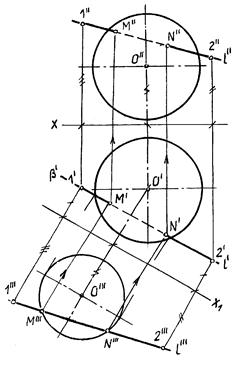
Рис.8.36

Задачи на взаимное пересечение прямой линии с кривой поверхностью - задачи третьего типа могут быть сведены к задачам второго типа путем преобразования комплексного чертежа.

Пример 1 (рис.8.37). Найти точки M и N пересечения прямой l с цилиндрической поверхностью вращения.

Решение:

Преобразуем заменой плоскостей проекций чертеж так, чтобы цилиндрическая поверхность стала проецирующей.

Одновременно с этим прямая l (1,2) преобразуется в линию l^IV(1^IV,2^IV), точки пересечения которой с очерком цилиндрической поверхности - M^IV и N^IV и будут искомыми.

Обратным преобразованием найдем эти точки на исходных проекциях

Построения ясны из чертежа.

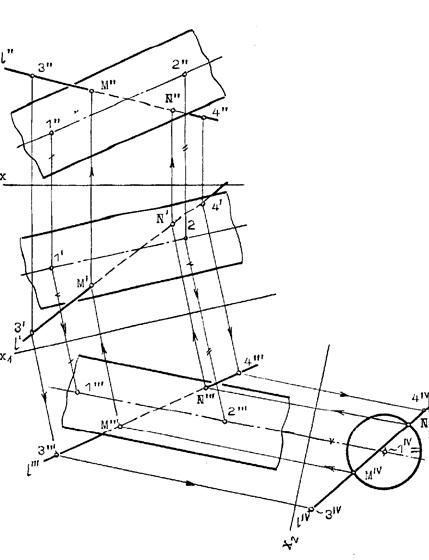
Рис.8.37

9. ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ КРИВЫХ ПОВЕРХНОСТЕЙ

Для построения линий взаимного пересечения двух кривых поверхностей пользуются методом вспомогательных секущих поверхностей. В качестве которых используются не только вспомогательные секущие плоскости, но и вспомогательные секущие поверхности: цилиндрические, конические и сферы, выбор которых в качестве “посредников” позволяет находить точки искомой линии пересечения.

1. Возможности применения способа вспомогательных секущих плоскостей в качестве “посредников”.

Вспомогательные секущие плоскости применимы, если заданы:

- две поверхности вращения, оси которых перпендикулярны к одной из плоскостей проекций;

- два цилиндра или два конуса, или конус и цилиндр;

- две линейчатые поверхности с общей плоскостью параллелизма;

- две каркасные поверхности.

Пример 1(рис.9.1). Построить линию пересечения сферы с конусом.

Решение:

1. Находим характерные и опорные точки искомой линии пересечения.

Такими точками будут точки пересечения очерковых образующих: А, В, С и С₁. Точки С и С₁ получены с помощью вспомогательной секущей плоскости g, проходящей через экватор сферы.

2. Промежуточные точки искомой линии находим с помощью семейства вспомогательных секущих плоскостей: g₁, g₂,...

3. Соединяя последовательно найденные точки А, М, С, N,..В получаем проекции искомой линии.

4. Определяем видимость.

Рис.9.1

Пример 2 (рис.9.2). Построить линию взаимного пересечения поверхностей цилиндра и тора.

Решение:

Обе заданные поверхности имеют общую плоскость симметрии, параллельную фронтальной плоскости проекций и потому точки искомой линии пересечения можно найти с помощью вспомогательных секущих плоскостей: b, b₁, b₂,...

Построение начинаем с опорных точек А и В искомой линии, принадлежащих очерковым образующим.

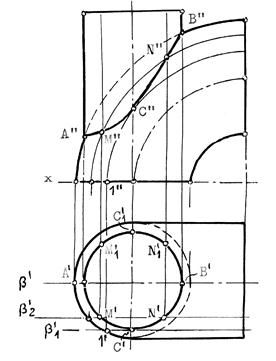
Рис.9.2

2. Возможности применения вспомогательных секущих сфер в качестве “посредников”.

Применение вспомогательных секущих сфер возможно в следующих случаях, когда на чертеже заданы:

1. Две поверхности вращения, оси которых пересекаются и параллельны одной из плоскостей проекций;

2. Две поверхности вращения, оси которых пересекаются, но ось одной из них параллельны, а ось другой - перпендикулярна к одной и той же плоскости проекций.

3. Когда на чертеже заданы две поверхности с общей плоскостью симметрии и одна из них является поверхностью вращения, а другая поверхность имеет семейство плоских круговых сечений, перпендикулярных общей плоскости симметрии.

Рассмотрим эти случаи на примерах.

Если на чертеже заданы две поверхности вращения, оси которых пересекаются и параллельны плоскости чертежа, то точки искомой линии пересечения могут быть найдены с помощью вспомогательных секущих концентрических сфер с центром в точке пересечения осей.

Пример 1 (рис.9.3). Построить линию пересечения поверхности конуса вращения с тором.

Решение:

Из точки О пересечения осей опишем некоторую сферу радиуса R. Она пересечет конус по двум параллелям: 1-1 и 2-2, а тор - по 3-3. Общие точки Е и Е пересечения параллелей 1-1 и 3-3 будут точками искомой линии пересечения заданных поверхностей.

По аналогии, описывая новые сферы, получим необходимое и достаточное количество точек искомой линии пересечения.

Примечание.

Сфера минимального радиуса R₁ будет касаться одной из поверхностей вращения и пересекать другую. В данном случае, она касается конуса и пересекает тор по параллели 4-4.

Точки С и С₁ получены с помощью вспомогательной горизонтальной плоскости g, проведенной через ось тора.

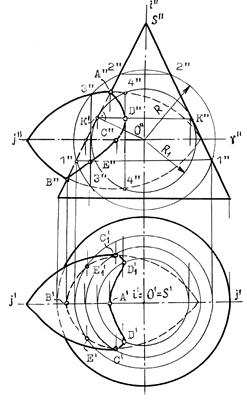
Рис.9.3

Идея применения способа вспомогательных секущих сфер основана на свойстве взаимного пересечения двух соосных поверхностей вращения, то есть имеющих общую ось вращения, по общим для них параллелям (рис.9.4).

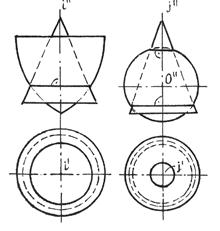
Рис.9.4

Пример 2 (рис.9.5). Построить линию взаимного пересечения поверхностей конуса и тора.

Решение:

В данном случае ось конуса параллельна, а ось тора - перпендикулярна горизонтальной плоскости проекций. Поэтому очерки вспомогательной секущей сферы некоторого радиуса Р нужно провести из точки О пересечения осей заданных поверхностей на той и другой плоскостях проекций. При этом на фронтальной проекции фигур сфера пересечет тор по параллели 1-1, а на горизонтальной плоскости проекций эта же сфера пересечет конус по параллелям 2-2 и 3-3. Поскольку окружность 1-1 проецируется на горизонтальную плоскость проекций в истинную величину, а параллели конуса - в прямые линии, то точки М и М пересечения этих линий и будут искомыми точками линии пересечения.

Аналогично можно найти необходимое и достаточное количество точек для построения проекций линии пересечения поверхностей.

Рис.9.5

Пример 3 (рис.9.6). Построить линию взаимного пересечения поверхностей двух торов.

Решение: Обе заданные поверхности имеют общую плоскость симметрии, параллельную фронтальной плоскости проекций. Причем открытый (тор-кольцо) имеет семейство круговых сечений, перпендикулярных плоскости симметрии. Это третий из рассматриваемых случаев, когда невозможно применение вспомогательных секущих сфер в качестве “посредников”.

Нахождение точек искомой линии пересечения заданных поверхностей начинаем с определения опорных точек А и В, в интервале между которыми расположится искомая линия пересечения поверхностей.

Выбираем на поверхности тора-кольца произвольное круговое сечение 1-1, лежащее в плоскости, проходящей через ось j вращения тора-кольца. Из центра С₁ восставим перпендикуляр к линии 1-1, который пересечет ось второго тора в точке О₁.

Из точки О₁ опишем сферу радиуса О₁-1, пересекающую второй тор по окружности 2-2.

Общие точки М и М₁ окружностей 1-1 и 2-2 и будут точками искомой линии пересечения заданных поверхностей.

Таким же способом найдены точки N и N₁ и другие не указанные точки.

Рис.9.6

ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА

Две поверхности второго порядка пересекаются по кривой четвертого порядка.

На общую плоскость симметрии поверхностей кривая их пересечения проецируется кривой второго порядка.

Дата добавления: 2014-01-11