Метод парных сравнений

Метод можно описать следующим образом. Допустим, заданы элементы одного, скажем 4-го уровня иерархии – A,B,C,D и один элемент E следующего более высокого уровня (3-его). Нужно сравнить элементы 4-го уровня попарно по силе их влияния на E, поместить числа, отражающие достигнутое при сравнении согласия во мнениях, в матрицу (матрицу парных сравнений) и найти собственный вектор с наибольшим собственным значением. Собственный вектор обеспечивает упорядочение приоритетов, а собственное значения является мерой согласованности суждений.

Освещен ность	А	В	С	D
А
В	1/5
С	1/6	1/4
D	1/7	1/6	1/4

Условимся, что числа в матрице определяются следующим образом:

А и В одинаково важны, заносим 1 в позицию (А,В).

А незначительно важнее, чем В, заносим 3.

А значительно важнее В, заносим 5.

А явно важнее В, заносим 7.

А по своей значительности абсолютно превосходит В, заносим 9.

Так как при сравнении элемента с самим собой имеем равную значительность, таким образом на главной диагонали должны стоять единицы. Если в позиции (А,В) мы записали число d, то в позиции (В,А) должно стоять число 1/d.

Полученную матрицу необходимо проверить на согласованность суждений. В общем случае под согласованием подразумевается то, что при наличии некоторого числа суждений (основных), все другие данные логически могут бать получены из них.

Для проведения парных сравнений n объектов, при условии, что каждый объект представлен в данных, по крайней мере, один раз, требуется (n-1) суждений о парных сравнениях. Из них можно просто вывести все остальные суждения, используя следующие отношения: если объект А1в 5 раза превосходит объект B и в 6 раз превосходит C, то А1=5B и А1=6C. Следовательно, 5B=6C или B=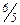C и C=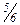B. Если численное значение суждения в позиции (B,C) не равно 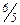, то матрица будет несогласованной. Это случается часто и не является бедствием. Для большинства задач очень трудно определить (n-1) суждений связывающих все объекты или виды действия, одно из которых является абсолютно верным.

Так как данные в нашей матрице весьма приближенные, можно получить грубые оценки этого вектора следующими 4-мя способами, которые расположены в порядке увеличения точности:

Суммировать элементы каждой строки и нормировать делением каждой суммы на сумму всех элементов, (сумма полученных результатов = 1). Первый элемент результирующего вектора будет приоритетом первого объекта, 2-ой - 2-ого и т.д.

Суммировать элементы каждого столбца и получить обратные величины этих сумм. Нормировать их так, чтобы их сумма равнялась единице (разделить каждую обратную величину на сумму всех обратных величин).

Разделить элементы каждого столбца на сумму элементов этого столбца (то есть нормировать столбец), затем сложить элементы каждой полученной строки и разделить эту сумму на число элементов строки Это - процесс нормированности столбца.

Умножить n элементов каждой строки и извлечь корень n-степени, нормировать полученные числа.

Если матрица согласована, то методы 1-4 дают один и тот же результат. В общем случае, когда матрица не согласованна эти методы дают различные результаты.

Известно, что согласованность положительной обратносимметричной матрицы эквивалентно требованию max= n, где max- максимальное собственное значение матрицы. Насколько плоха согласованность для конкретной задачи можно оценить путем сравнения значения величины (max- n)/(n-1) с ее значением из случайно выбранных суждений и соответствующих обратных величин матрицы того же разряда. Подробнее согласование рассмотрим ниже.

Умножив матрицу сравнений на полученную оценку вектора решения, получим новый вектор.

Разделив первую компоненту этого вектора на первую компоненту оценки вектора решения, вторую на вторую и т.д., определим еще один вектор.

Разделив сумму компонент этого вектора на число компонент найдем приближение для max.Чем ближе max к n (числу объектов или видов действия в матрице), тем более согласован результат.

Отклонение от согласованности может быть выражено величиной (max- n)/(n-1), которую назовем индексом согласованности (ИС).

Вводится еще одна величина –

ИС/СИ,где СИ - случайный индекс по шкале от 1 до 3 обратносимметричной матрицы (имеются соответствующие таблицы).

Таблица

Размерность матрицы
СИ		0,58	0,9	1,12	1,24	1,32	1,41	1,45	1,49	1,51	1,48	1,56	1,57	1,59

Отношение ИС/СИ называется отношением согласованности (ОС). Значение ОС меньше или равное 0,1 будем считать приемлемым.

Эти сравнения и вычисления устанавливают приоритеты элементов некоторого уровня иерархии относительно одного элемента следующего уровня. Если уровней больше, чем два, то различные векторы приоритетов могут быть объединены в матрицы приоритетов, из которых определяется один окончательный вектор приоритетов для нижнего уровня.

Дата добавления: 2014-01-13