Несобственные интегралы

п1. Несобственный интеграл по бесконечному промежутку.

Пусть функция f (x) определена на полуоси 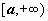и интегрируема по любому отрезку [ a, b ], принадлежащему этой полуоси. Предел интеграла 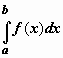при 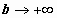называется несобственным интегралом функции f (x) от a до 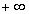и обозначается .
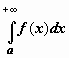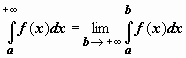Итак, по определению, . Если этот предел существует и конечен, интеграл 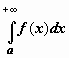называется сходящимся; если предел не существует или бесконечен, интеграл называется расходящимся.
Примеры: 1. 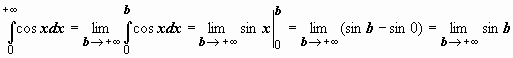; этот предел не существует; следовательно, исследуемый интеграл расходится.
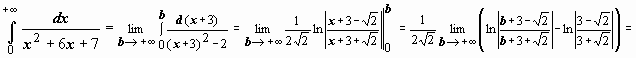
2. 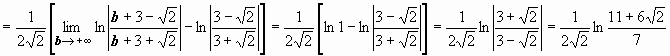; следовательно, интеграл сходится и равен .
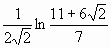Аналогично интегралу с бесконечным верхним пределом интегрирования определяется интеграл в пределах от 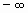до b: 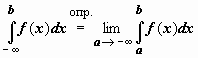и в пределах от 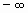до 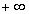: 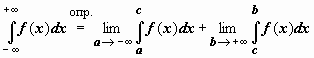. В последнем случае f (x) определена на всей числовой оси, интегрируема по любому отрезку; c - произвольная (собственная) точка числовой оси; интеграл называется сходящимся, если существуют и конечны оба входящих в определение предела. Пользуясь свойством аддитивности определённого интеграла, можно показать, что существование конечных пределов и их сумма не зависят от выбора точки c.
Примеры: 3. 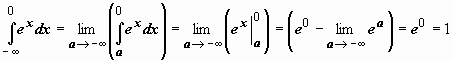. Интеграл сходится.
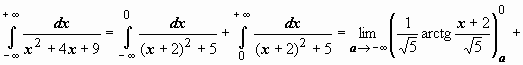
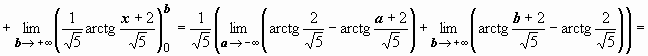
4. 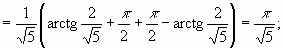следовательно, интеграл сходится и равен .
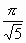Очевидно следующее утверждение, которое мы сформулируем для интеграла с бесконечным верхним пределом: 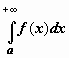сходится тогда и только тогда, когда для любого c, удовлетворяющего неравенству c > a, сходится интеграл 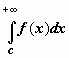(док-во: так как при a < c < b по свойству аддитивност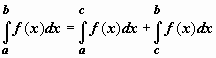и , и 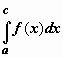от b не зависит, то конечный предел при 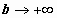для интеграла в левой части существует тогда и только тогда, когда существует конечный предел для интеграла в правой части равенства).
Формула Ньютона-Лейбница для несобственного интеграла.

В приведённых примерах мы сначала вычисляли с помощью первообразной функции определённый интеграл по конечному промежутку, а затем выполняли предельный переход. Объединим два этих действия в одной формуле. Символом 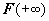будем обозначать ; символом 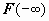- соответственно, 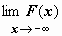; тогда можно записать 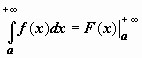, , 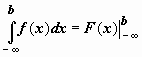, 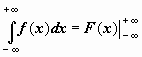подразумевая в каждом из этих случаев существование и конечность соответствующих пределов. Теперь решения примеров выглядят более просто: 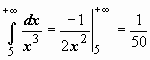- интеграл сходится; 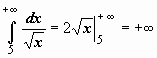- интеграл расходится.

Для несобственных интегралов применимы формулы интегрирования по частям и замены переменной: 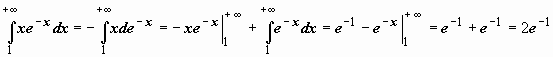; при замене переменной несобственный интеграл может преобразовываться в собственный. Так, например, вычислим интеграл: 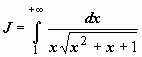. Пусть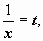 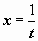, 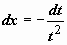; если 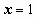, то 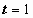; если 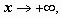то 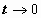; 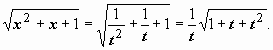Поэтому 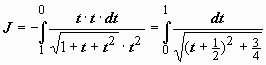(это уже собственный интеграл) = .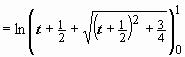

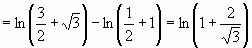п2. Несобственный интеграл от неограниченной функции.
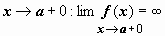Пусть функция f (x) определена на полуинтервале (a, b ], интегрируема по любому отрезку , и имеет бесконечный предел при . Несобственным интегралом от f (x) по отрезку [ a, b ] называется предел 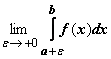. Если этот предел конечен, говорят, что интеграл сходится; если предел не существует или бесконечен, говорят, что интеграл расходится.
Примеры: 17. 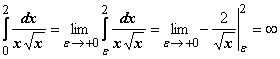- интеграл расходится;
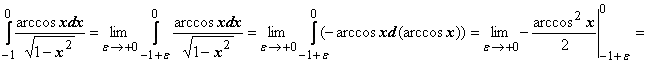
18. 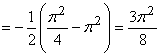- интеграл сходится.

Если для функции f (x) на полуинтервале (a, b ] существует первообразная F (x), то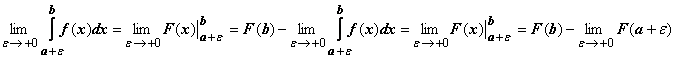, и сходимость интеграла определяется наличием или отсутствием конечного предела 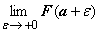. Будем писать просто 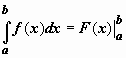, имея в виду, что если соответствующий предел конечен, то интеграл сходится, в противном случае - расходится.
Примеры: 19. 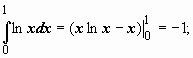(интеграл сходится).
20. 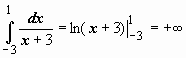(интеграл расходится).
В следующих дальше случаях неограниченности функции будем поступать аналогично.

Пусть функция f (x) определена на полуинтервале [ a, b), интегрируема по любому отрезку 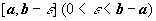, и имеет бесконечный предел при 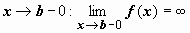. Несобственным интегралом от f (x) по отрезку [ a, b ] называется предел 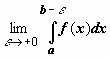. Если этот предел конечен, говорят, что интеграл сходится; если предел не существует или бесконечен, говорят, что интеграл расходится.

Пусть функция f (x) определена на отрезке [ a, b ], имеет бесконечный предел при стремлении аргумента к какой-либо внутренней точке c этого отрезка: 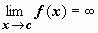, интегрируема по любому отрезку, не содержащему точку c. Несобственным интегралом от f (x) по отрезку [ a, b ] называется 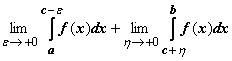. Интеграл сходится, если оба эти пределы существуют и конечны, в противном случае интеграл расходится.

РАЗДЕЛ IX. Дифференциальное исчисление функций нескольких переменных.

Дата добавления: 2014-01-13