Признаки сходимости числовых рядов

Теорема (необходимое условие сходимости ряда). Если ряд сходящийся, то предел его общего члена равен нулю .

Следствие. Если 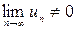, то ряд расходящийся.

Замечание. Условие является необходимым условием сходимости ряда, но не достаточным, то есть выполнение этого условия не гарантирует сходимости ряда.

Первый признак сравнения. Пусть члены рядов и удовлетворяют условию п =1,2,3,…. Тогда, если ряд сходящийся, то сходящийся и ряд , а если ряд расходящийся, то расходящийся и ряд .

Второй признак сравнения. Пусть члены рядов и положительны, причём существует конечный предел . Тогда оба ряда сходятся или расходятся одновременно.

Сравнивать ряды удобно с рядами и , сходимость которых известна.

Ряд является суммой бесконечной геометрической прогрессии. Он сходится при (когда прогрессия убывающая) и расходится при .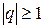

Ряд называется обобщенным гармоническим рядом. Он сходится при 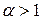и расходится при .

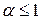Признак Даламбера. Если для членов ряда с положительными членами существует предел , то ряд будет сходящимся при 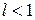и расходящимся при .

Радиальный признак Коши. Если для членов ряда с положительными членами существует предел 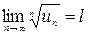, то ряд будет сходящимся при 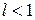и расходящимся при .

Интегральный признак Коши. Если , где 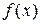– положительная невозрастающая непрерывная функция, то ряд и интеграл сходятся или расходятся одновременно.

§ 3. Знакочередующиеся ряды

Опр. 1. Знакочередующимися называют ряды, в которых знаки членов строго чередуются 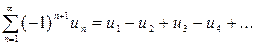(1), где .

Признак Лейбница. Если для членов ряда (1) выполняется два условия:

1) ,

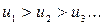2) ,

то этот ряд сходится, его сумма положительна и не превышает .

Следствие. Если сумму S сходящегося ряда (1) заменить суммой S_n его п первых членов, то допущенная при этом погрешность не превышает абсолютной величины первого из отброшенных членов, то есть .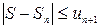

Это следствие широко используется при приближённых вычислениях.

Опр. 2. Знакопеременными называются ряды, у которых члены имеют разные знаки.

Опр. 3. Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд , составленный из абсолютных величин его членов.

Опр. 4. Знакопеременный ряд называется условно сходящимся, если он сходящийся, а ряд, составленный из абсолютных величин его членов, расходящийся.

Теорема 1. Любой абсолютно сходящийся ряд сходится.

Теорема 2. Абсолютно сходящийся ряд остаётся абсолютно сходящимся при произвольной перестановке его членов. При этом сумма ряда не зависит от порядка его членов.

Теорема 3. Члены условно сходящегося ряда всегда можно переставить так, чтобы его сумма равнялась наперёд заданному числу. Более того, можно так переставить члены условно сходящегося ряда, что новый ряд будет расходящимся.

§ 4. Функциональные ряды

Опр. 1. Ряд 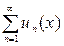, членами которого являются функции от х, называется функциональным рядом.

Давая переменной х конкретные числовые значения, получим разные числовые ряды, которые могут быть сходящимися или расходящимися.

Опр. 2. Множество всех значений х, для которых ряд 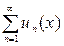сходящийся, называется областью сходимости этого ряда.

Опр. 3. Функциональный ряд вида (1) где х₀, а₀ – числа, называется степенным рядом.

Переобозначив х-х₀ на х, ряд (1) всегда можно свести к виду (2).

Для простоты будем изучать ряды вида (2). Ряд (2) всегда сходится, по крайней мере, в точке х =0.

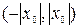Теорема Абеля. Если ряд (2) сходящийся при х=х₀≠0, то он абсолютно сходящийся для всех значений х, что удовлетворяют неравенству , то есть в интервале . Если при х=х₁ ряд (2) расходящийся, то он расходящийся для всех значений х, что удовлетворяют неравенству .

Из теоремы Абеля следует, что если ряд (2) сходится хотя бы в одной точке х=х₀≠0, то существует такое число R >0, что при ряд сходится абсолютно, а при 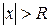расходится. Это число R называют радиусом сходимости степенного ряда, а интервал (-R,R) – его интервалом сходимости.

Радиус сходимости ряда (2) можно найти по формулам

или . (3)

Вывод. Чтобы найти область сходимости ряда (2) надо:

1) найти интервал сходимости (-R,R) ряда, применяя к ряду признаки Даламбера и Коши, или пользуясь формулами (3);

2) исследовать сходимость ряда на концах интервала сходимости, то есть в точках x= ± R.

Дата добавления: 2014-01-13