Применение степенных рядов при приближенных вычислениях значения функции

Ряды широко используются для приближённого вычисления функций, интегралов, для приближённого интегрирования дифференциальных уравнений.

Пусть надо найти f(x₀) для функции f(x), которая раскладывается в степенной ряд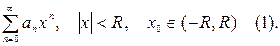

Тогда Заменяя значение f(x₀) суммой n членов этого ряда получаем приближенное значение f(x₀), при этом ошибка равна В силу сходимости ряда (1) в точке х=х₀, при достаточно большом n эта ошибка станет сколь угодно малой и S_n дает значение f(x₀) с любой наперед заданной точностью. Для вычисления f(x₀) с заданной точностью надо уметь производить оценку остатка (2), что позволяет брать требуемое число членов в S_n.

Оценка остатка ряда особенно проста, если ряд удовлетворяет признаку Лейбница. В этом случае остаток имеет знак своего первого члена и по абсолютной величине меньше его.

В случае произвольного ряда абсолютная величина R_n не превосходит суммы абсолютных величин членов, входящих в R_n. Для уже полученного положительного ряда стараются найти легко суммируемый ряд из положительных членов, члены которого были бы меньше абсолютных величин членов остатка, и оценивают остаток суммой этого ряда.

§ 7. Ряды Фурье

Ряды Фурье играют большую роль в математической физике, теории упругости, электротехнике и особенно их частный случай – тригонометрические ряды Фурье.

Опр. 1. Тригонометрическим рядом называют ряд вида

или, символической записи: (1)

где ω, a₀, a₁, …, a_n, …, b₀, b₁, …,b_n, … – постоянные числа (ω >0).

Ряд (1) сходится в некоторой точке х₀, в силу периодичности функций 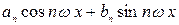(n =1,2,..), он окажется сходящимся и во всех точках вида (m – любое целое число), и тем самым его сумма S(x) будет (в области сходимости ряда) периодической функцией. Если S_n(x) – n -я частичная сумма этого ряда, то имеем

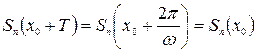
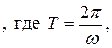
а потому и 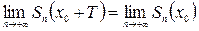, т. е. S(x₀+T)=S(x₀). Поэтому, говоря о разложении некоторой функции ƒ(x) в ряд вида (1), будем предполагать ƒ(x) периодической функцией.

Пусть периодическая функция ƒ(х) с периодом 2π такая, что она представляется тригонометрическим рядом, сходящимся к данной функции в интервале (-π, π), т. е. является суммой этого ряда:

ƒ(x)= (2).

Предположим, что интеграл от функции, стоящей в левой части этого равенства, равняется сумме интегралов от членов этого ряда. Это будет выполняться, если предположить, что числовой ряд, составленный из коэффициентов данного тригонометрического ряда, абсолютно сходится, т. е. сходится положительный числовой ряд

.

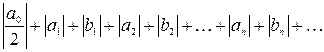Ряд (1) мажорируем и его можно почленно интегрировать в промежутке (-π, π). Проинтегрируем обе части равенства (2):

.

Вычислим отдельно каждый интеграл, встречающийся в правой части:

, , .

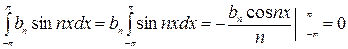Таким образом, , откуда .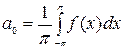

Из определения четной и нечетной функции следует, что если ψ(x) четная функция, то . Аналогично можно доказать, что если ψ(x) нечетная функция, то .

Если в ряд Фурье разлагается нечетная функция ƒ(x), то произведение ƒ(x) cos kx есть функция также нечетная, а ƒ(x) sin kx – четная; следовательно,

т. е. ряд Фурье нечетной функции содержит «только синусы».

Если в ряд Фурье разлагается четная функция, то произведение ƒ(x)sin kx есть функция нечетная, а ƒ(x)cos kx – четная, то:

т. е. ряд Фурье четной функции содержит «только косинусы».

Полученные формулы позволяют упрощать вычисления при разыскании коэффициентов Фурье в тех случаях, когда заданная функция является четной или нечетной. Очевидно, что не всякая периодическая функция является четной или нечетной.

Опр. 2. Функция ƒ(x) называется кусочно-монотонной на отрезке [ a, b ], если этот отрезок можно разбить конечным числом точек х₁, х₂, …,х_n-1 на интервалы (а, х₁), (х₁, х₂),…, (х_n-1, b) так, что на каждом из интервалов функция монотонна, т. е. либо не возрастающая, либо неубывающая.

Теорема. Если периодическая функция ƒ(x) с периодом 2π – кусочно монотонная и ограниченная на отрезке [-π, π], то ряд Фурье, построенный для этой функции, сходится во всех точках. Сумма полученного ряда S(x) равна значению функции ƒ(x) в точках непрерывности функции. В точках разрыва функции ƒ(x) сумма ряда равняется среднему арифметическому пределов функции ƒ(x)справа и слева, т. е. если х = с – точка разрыва функции ƒ(x), то

Раздел XIII. Теория функции комплексного переменного

Дата добавления: 2014-01-13