Интегрируемые типы дифференциальных уравнений второго порядка

Задача Коши

Задача нахождения решения дифференциального уравнения, удовлетворяющего условиям: 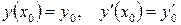, где 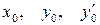‑ заданные числа, называется задачей Коши. Эти условия часто называют начальными условиями, так как с экономической точки зрения они означают, что в фиксированный момент времени задано начальное состояние экономического процесса и скорость его изменения.

Геометрический смысл задачи Коши состоит в нахождении интегральной кривой, проходящей через заданную точку и имеющей заданный угловой коэффициент касательной в этой точке.

Пример. Решить задачу Коши .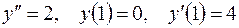

Найдем все решения данного уравнения. Интегрируем: , .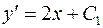

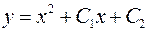Воспользовавшись начальными условиями, определим значение констант 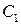и 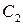из системы уравнений:

.

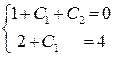Следовательно, 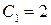, 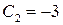и искомое решение: .

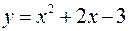В общем случае дифференциальное уравнение второго порядка не решается аналитически, однако, в некоторых случаях, дифференциальные уравнения второго порядка определенных типов решаются с применением операции неопределенного интегрирования.

Тип I.

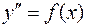
Интегрируя, получим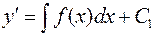

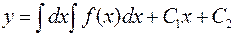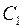Интегрируя еще раз, окончательно получим , где и 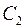– произвольные постоянные, и неопределенные интегралы трактуются как некоторые первообразные соответствующих функций.

Тип II.

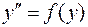
Положим, 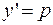. Отсюда, рассматривая 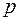как функцию от , будем иметь

.

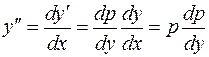Следовательно, уравнение 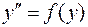примет вид 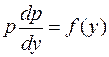. Разделяя переменные, получим

.

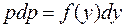Интегрируя последнее уравнение, находим

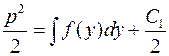или .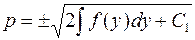

Так как 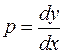, то 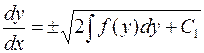. Отсюда, разделяя еще раз переменные и интегрируя, получим

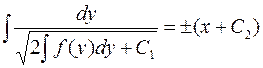
Тип III.

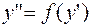
Положим 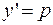, тогда 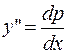. Уравнение 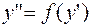примет вид

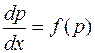
Разделяя переменные и интегрируя, получим

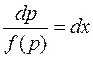
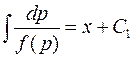
Определив из этого уравнения величину 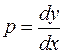, путем вторичного интегрирования можно найти и .

Дата добавления: 2014-01-13