Локальные и глобальные экстремумы

Классификация задач оптимизации

Ограничения неравенства

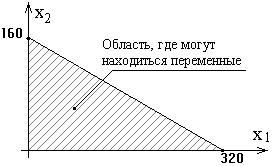
Система ограничений-неравенств определяет область допустимых значений переменных.

Пример: 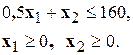Количество ограничений-неравенств может быть любым.

Общая форма записи ограничений-равенств:

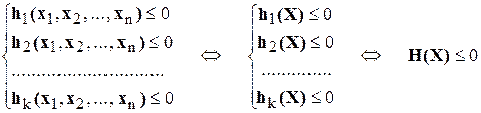
1) Условная и безусловная оптимизация. Безусловная оптимизация – это решение задачи при отсутствии любых ограничений, а условная оптимизация – при наличии ограничений.

2) Линейная и нелинейная оптимизация. Если критерий оптимизации, ограничения-равенства и ограничения-неравенства, являются линейными функциями, в этом случае применяются методы линейной оптимизации. Если хотя бы одна функция является нелинейной, то эта задача нелинейная.

3) Одномерные и многомерные методы. Одномерные используются в том случае, если количество переменных равно единице (одна переменная), а многомерные – количество переменных больше единицы. Многие методы многомерной оптимизации (особенно нелинейной) используют одномерные методы.

4) Методы непрерывной и дискретной (целочисленной) оптимизации. Дискретные методы используются в том случае, если переменные могут принимать не любые значения, а только из определенного набора.

5) Прямые и косвенные методы. Прямые методы используют для поиска максимума только значения функции f(X), вычисленные в определенных точках. Косвенные методы используют для поиска максимума не только значения функции f(X), но и ее производные или аппроксимацию другими функциями.

6) Метод динамического программирования. Этот метод используются для оптимизации процессов, протекающих во времени или развивающихся в пространстве.

Локальным минимумом называется точка, в небольшой окрестности которой значение функции является наименьшим. Для локального максимума определение аналогично.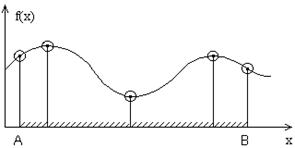

Глобальным минимумом (максимумом) называется точка, в которой значение функции минимально (максимально) на всей допустимой области.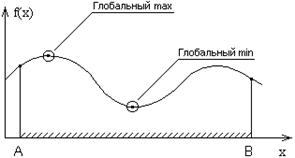

Задачи на определение локального максимума (минимума) называют экстремальными. В математическом анализе для отыскания экстремумов функции используется условие 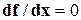. Так как решение этого уравнения представляет собой проблему такой же сложности, что и исходная задача, а во многих случаях невозможно вычисление и самой производной 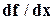(например, для таблично заданных функций), то для решения оптимизационных задач используются специальные методы, не требующие вычисления производных.

Нет универсального метода для поиска глобального минимума или максимума (за небольшим исключением, например, случай линейных функций или метод непосредственного перебора значений функции). Поэтому на практике сначала находят точки локальных экстремумов (минимумов и максимумов), а затем, сравнивая их между собой, определяют глобальный минимум или максимум.

Дата добавления: 2014-01-13