Лекция № 17 Бескооалиционные игры или игры 2-х лиц с произвольной суммой

В конечной бескоалиционной игре двух игроков (КБИДИ)каждый из них делает один ход – выбирает одну стратегию из имеющегося у него конечного числа стратегий, и после этого он получает свой выигрыш согласно определённым для каждого из них матрицами выигрышей. Другими словами КБИДИ полностью определяется двумя матрицами выигрышей для двух игроков. Поэтому такие игры называются биматричными. Пусть у игрока 1 имеется m стратегий, i =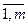, у игрока 2 имеется n стратегий, j =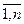. Выигрыши игроков 1 и 2 соответственно задаются матрицами

А = 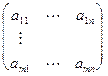, В =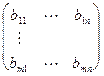

Будем по-прежнему считать полный набор вероятностей x = (x₁,..., x_m) применения 1 игроком своих чистых стратегий смешанной стратегией игрока 1, и у = (y₁,..., y_n) – смешанной стратегией игрока 2. тогда средние выигрыши игроков 1 и 2 соответственно равны

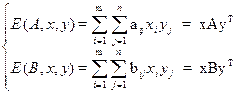
Ситуация равновесия для биматричной игры составляет пару (x,y) таких смешанных стратегий игроков 1 и 2, которые удовлетворяют неравенствам:

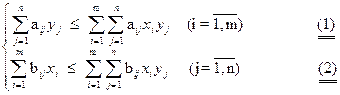
или

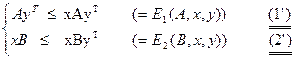
Для определения ситуаций равновесия необходимо решить систему неравенств (1) и (2) (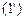и 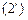) относительно неизвестных x = (x₁,..., x_m) и у = (y₁,..., y_n) при условиях

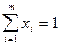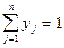, , x_i ³ 0 (i =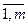), y_j ³ 0 (j =).

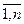Теорема (Нэша). Каждая биматричная игра имеет по крайней мере одну ситуацию равновесия.

Содержательно это означает, что решения системы (1) и (2) включают для игрока 1 множество К – решений, а для игрока 2 множество L – решений.

Множество К решений системы (1) – (2) состоит из

1) всех ситуаций вида (0; y), если a₁y - a₂ £ 0; 0 £ y £ 1;

2) всех ситуаций вида (x; y), если a₁y - a₂ = 0; 0 < x < 1;

3) всех ситуаций вида (1; y), если a₁y - a₂ ³ 0; 0 £ y £ 1.

Множество L приемлемых для него ситуаций состоит из:

1) всех ситуаций вида (x, 0), если b₁x - b₂ < 0; 0 £ x £ 1,

2) всех ситуаций вида (x, y), если b₁x - b₂ = 0; 0 £ x £ 1; 0 < y < 1,

3) всех ситуаций вида (x, 1), если b₁x - b₂ > 0; 0 £ x £ 1.

Решением игры является пересечение множеств K и L, т.е. те значения x и y, которые являются общими для множеств K и L.

y y

1 1

x x

0 1 0 1

а) б)

При этом зигзаги K и L могут быть не только одинаковой, но и противоположной направленности. В первом случае зигзаги имеют одну точку пересечения, а во-втором ­­­– три. Средние выигрыши при этом определяются по формулам (*), если в них подставить полученное решение x и y (рис.а)). Очевидно a входит в смешанную стратегию игрока 2, хотя зависит только от выигрышей 1 игрока; b входит в смешанную стратегию игрока 1, хотя зависит только от выигрышей игрока 2. Сравнение этих результатов с результатами решения матричных игр с нулевой суммой показывает, что a совпадает с оптимальной стратегией игрока 1 в матричной игре с матрицей A, а b – с оптимальной стратегией игрока 2 в матричной игре с матрицей B. Отсюда можно сделать вывод, что равновесная ситуация направляет поведение игроков не только на максимизацию своего выигрыша, сколько на минимизацию выигрыша противника.

С другой стороны, естественно также рассматривать подходящим, поведение игроков в конечных бескоалиционных играх, направленное на максимизацию своего выигрыша с учётом максимального противодействия игрока,т.е. подходящей стратегией игрока 1, считать оптимальную смешанную стратегию игрока 1 в матричной игре с матрицей A, а подходящей стратегией игрока 2, считать оптимальную смешанную стратегию игрока 2 в матричной игре с матрицей B, если в ней рассматривать решение с позиций максимизации выигрыша игрока 2, т.е. решать её, как для игрока 1, с матрицей .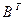

Пример1. Министерство желает построить один из двух объектов на территории города. Городские власти могут принять предложения министерства или отказать. Министерство – игрок 1 – имеет две стратегии: строить объект 1, строить объект 2. Город – игрок 2 – имеет две стратегии: принять предложение министерства или отказать. Свои действия (стратегии) они применяют независимо друг от друга, и результаты определяются прибылью (выигрышем) согласно следующим матрицам:

A = , B =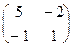

(например: если игроки применяют свои первые стратегии, министерство решает строить 1 объект, а городские власти разрешают его постройку, тогда город получает выигрыш 5 млн, а министерство теряет 10 млн, и т.д.)

Решение. Для этой игры имеем:

a₁ = a₁₁ - a₁₂ - a₂₁ + a₂₂ = -10 - 2 - 1 - 1 = -14 < 0,

a₂ = a₂₂ - a₁₂ = -1 - 2 = -3,

.

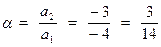Так как a₁ < 0, то множество решений K имеет следующий вид:

(0, y) при 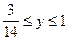; (x, 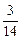) при 0 £ x £ 1; (1, y) при 0 £ y £ .

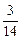Для 2 игрока имеем:

b₁ = b₁₁ - b₁₂ - b₂₁ + b₂₂ = 5 + 2 + 1 + 1 = 9 > 0,

b₂ = b₂₂ - b₂₁ = 1 + 1 = 2,

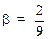
y

Так как b₁ > 0, то множество решений L L

имеет следующий вид:

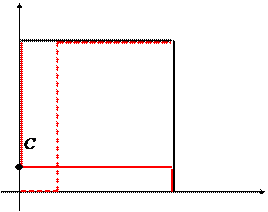
K

(x; 0), при 0 £ x £;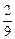

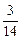
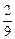(; y), при 0 £ y £ 1; 0 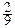1 x

(x; 1), при 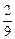£ x £ 1.

Точка пересечения множеств L и K есть точка C с координатами x = 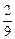; y = 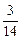и является соответственно приемлемыми стратегиями министерства и города.

При этом выигрыш соответственно равен

E₁ (A,x,y) = (x, 1- x)=

= =

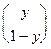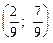
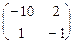
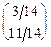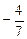
E₂ (A,x,y) = (x, 1- x)=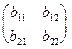

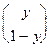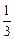
Замечание. Если решить эту игру как матричные игры двух игроков с нулевой суммой, то для игры с матрицей A оптимальные смешанные для 1 игрока и цена игры получаются из решения уравнений

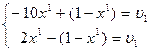
откуда вероятность применения игроком 1 первой стратегии равна 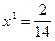, цена игры – , что совпадает с E₁, вероятность применения игроком 2 первой стратегии 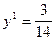; для игры с матрицей B оптимальные смешанные стратегии и цена игры для игрока 2 определяются из системы:

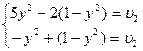
Следовательно, вероятность применения игроком 2 своей стратегии 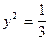, а игроком 1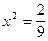, цена игры 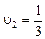, что совпадает с E₂.

Таким образом, если каждый из игроков будет применять свои стратегии в этой игре, исходя только из матриц своих выигрышей, то их оптимальные средние выигрыши совпадают с их выигрышами при ситуации равновесия.

Дата добавления: 2014-01-13