Сукупності та системи нерівностей з однією змінною

Оскільки нерівності з однією змінною є предикатами, то над ними можна виконувати всі операції логіки висловлень, зокрема диз’юнкцію і кон’юнкцію.

Диз’юнкція кількох нерівностей з однією змінною, які визначені на множині М, називається сукупністю нерівностей з однією змінною (позначається квадратною дужкою зліва). Кон’юнкція кількох нерівностей з однією змінною, що визначені на множині М, називається системою нерівностей з однією змінною (позначається фігурною дужкою зліва).

Поняття, що стосуються сукупностей і систем нерівностей з однією змінною, встановлюються на підставі властивостей диз’юнкції і кон’юнкції предикатів.

Область визначення сукупності (системи) нерівностей з однією змінною дорівнює перерізу областей визначення нерівності сукупності (системи). Множина розв’язків сукупності (системи) нерівностей з однією змінною дорівнює об’єднанню (перерізу) множин розв’язків кожної з нерівностей сукупності (системи).

Для знаходження множини розв’язків сукупності (системи) нерівностей з однією змінною потрібно розв’язати кожну з нерівностей, а потім знайти об’єднання (переріз) одержаних множин. Це й буде множина розв’язків сукупності (системи) нерівностей. Наприклад, множиною розв’язків сукупності нерівностей

буде множина R, бо перша нерівність має розв’язками проміжок [2; + ¥[, а друга – проміжок ]– ¥; 7[; множиною розв’язків системи нерівностей

є проміжок [2; 7[.

Як при розв’язуванні рівнянь і нерівностей з однією змінною, так і при розв’язуванні сукупностей і систем нерівностей важливу роль відіграє поняття рівносильності. Поняття рівносильності розглянемо лише для систем нерівностей з однією змінною, для сукупності нерівностей всі твердження будуть аналогічними, тільки відповідно сформульованими.

Системи нерівностей з однією змінною, що визначені на множині М, називаються рівносильними на ній, якщо їх множини розв’язків збігаються. Якщо системи не мають розв’язків, то вони також вважаються рівносильними. Рівносильність систем нерівностей з однією змінною залежить від їх області визначення: зміна її може привести до порушення рівносильності. Наприклад, системи нерівностей

i

рівносильні на множині додатних дійсних чисел і нерівносильні на множині дійсних чисел, бо на множині R₊ множинами розв’язків є числовий проміжок ] 2; + ¥[, а на множині R розв’язками першої системи є множина ]–¥; – 3[ È ]2; + ¥[, а другої –]–¥; –4[ È ]2; + ¥[.

Скориставшись теоремами про рівносильність нерівностей з однією змінною, неважко довести теорему.

Теорема 4. Якщо в системі нерівностей з однією змінною хоч одну з нерівностей замінити на їй рівносильну, то одержимо систему нерівностей, рівносильну заданій на її області визначення.

Задача 4. Розв’язати нерівність

Областю визначення нерівності будуть всі дійсні числа, що задовольняють умову 3х + 8 ¹ 0. Зведемо нерівність до простішого вигляду, користуючись теоремами про рівносильність нерівностей та наслідками з них:

Одержана нерівність, на основі залежності знаку частки від ділення двох довільних дійсних чисел, буде рівносильна сукупності систем нерівностей:

i

Щоб розв’язати сукупність систем нерівностей з однією змінною, потрібно розв’язати кожну нерівність системи, після цього знайти переріз множин розв’язків нерівностей кожної системи, а потім об’єднати множини розв’язків систем нерівностей. Одержана множина і буде множиною розв’язків даної сукупності систем нерівностей:

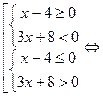
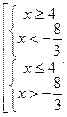
Для знаходження множини розв’язків першої системи сукупності зобразимо множину розв’язків кожної нерівності цієї системи на координатній прямій і знайдемо їх переріз (рис. 1).

Звідси одержуємо, що множина розв’язків першої системи порожня. Аналогічно діємо і при знаходженні множини розв’язків другої системи (рис. 2).

Одержуємо, що множиною розв’язків другої системи є числовий проміжок . Об’єднання знайдених множин буде числовим проміжком .

Відповідь: .

Задача 5. Розв’язати нерівність

4х² – 10х + 7 < 6х² – х + 2.

Областю визначення даної нерівності є множина дійсних чисел R. Користуючись теоремами про рівносильність нерівностей та наслідками з них, задану нерівність можна спростити:

4х² – 10х + 7 – 6х² + х – 2 < 0 Û –2х² – 9х + 5 < 0 Û 2х² + 9х – 5 > 0.

Одержали квадратну нерівність. Розв’язування її зводиться до знаходження множини значень змінної х, при якій квадратний тричлен з додатним старшим коефіцієнтом (у даному разі коефіцієнт дорівнює 2) більший за нуль. Для цього знайдемо його дискримінант і корені, якщо вони існують:

D = b² – 4ас = 9² –4×2×(–5) = 121 = 11², D > 0, а тому квадратний тричлен має два дійсних і різних корен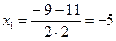і

і

Як відомо, графіком квадратного тричлена є парабола, вітки якої спрямовані вгору, якщо старший коефіцієнт додатний, і яка перетинає вісь Ох у точках х₁ = – 5 і х₂ = . Накреслимо схематично графік квадратного тричлена (рис. 3) і за його допомогою знайдемо множину значень змінної х, при якій він розміщений над віссю Ох. Ця множина і становитиме множину розв’язків даної нерівності.

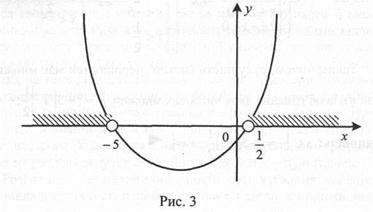
Отже, множиною розв’язків даної нерівності є об’єднання двох числових проміжків ]– ¥; – 5[ і ]; + ¥[.

Розв’язати нерівність

2х² + 9х – 5 > 0

можна також на підставі залежності знаку добутку двох довільних дійсних чисел від множників. Для цього розкладемо квадратний тричлен 2х² + + 9х – 5 на лінійні множники

2х² + 9х – 5 = 2(х + 5)(х – ) = (х + 5)(2х – 1).

Отже,

2х² + 9х – 5 > 0 Û (х + 5)(2х – 1) > 0.

Одержана нерівність буде рівносильна сукупності систем нерівностей

і

Знайдемо їх розв’язки:

Таким чином, сукупність систем нерівностей має множиною розв’язків об’єднання двох числових множин ]– ¥; – 5[ і ]; + ¥[.

Відповідь: х Î ]– ¥; – 5[ і ]; + ¥[.

Дата добавления: 2014-01-13